Содержание
- 2. 1. Определение логарифма. Основное логарифмическое тождество. 2.Основные свойства логарифмов. 3. Частные свойства.
- 4. Основные свойства логарифмов
- 6. Частные свойства:
- 7. Решение логарифмических уравнений
- 8. Что значит «решить уравнение»? Решить уравнение – это значит найти все его корни (решения) или установить,
- 9. Что такое корень уравнения? Корнем (решением) уравнения называется число, которое при подстановке в уравнение превращает его
- 10. Какие уравнения называют логарифмическим? Логарифмическим уравнением – уравнение, содержащие неизвестное под знаком логарифма.
- 11. Определение простейшего логарифмического уравнения: Уравнение вида log а х = в, где а ≠ 1 ,
- 12. метод решения с помощью определения логарифма; применение основного логарифмического тождества; метод потенцирования; метод введения новых переменных;
- 13. Метод решения с помощью определения логарифма Например, уравнение log а х = b (а > 0,
- 14. Метод решения с помощью определения логарифма ПРИМЕР: logх-18 =1 Решение: (х-1)1 = 8 х-1 = 8
- 15. Метод решения с помощью определения логарифма ПРИМЕР: 6) log7(50х-1) = 2 Решение: 72 = 50х-1 50х-1
- 16. Применение основного логарифмического тождества: alog a b =b (где b>0, a>0 и a≠1) Примеры: 1) 9x
- 17. Метод потенцирования Суть метода - переход от уравнения log а f( х)= log а g(х) к
- 18. Примеры на метод потенцирования 1) log3х = log39 Решение: 1) х=9 Проверка: подставим найденное значение x=9
- 19. 2) log7(2х-3) = log7х Решение: 2х-3=х; х=3 Проверка: подставим найденное значение x=3 в исходное уравнение log7(2.3-3)
- 20. 3) log 5 (2x+3)= log 5 (x+1) Решение: log 5 (2x+3)= log 5 (x+1) 2x+3= x+1;
- 21. 4) log 5 x= log 5 (6-x2) Решение: Проверка: 1) Ответ: 2. не существует -3 посторонний
- 22. Метод введения новых переменных Суть метода -приведение логарифмического уравнения к квадратному 1) ввести новую переменную 2)
- 23. Метод введения новых переменных Пример: 1) Ответ: ;
- 24. Метод введения новых переменных Решение: 2) , Ответ: 10
- 26. Скачать презентацию























 Определители второго и третьего порядка
Определители второго и третьего порядка Длина
Длина Логические задачи. Задачи со спичками
Логические задачи. Задачи со спичками Многогранники. Понятие многогранника. Призма
Многогранники. Понятие многогранника. Призма Множества
Множества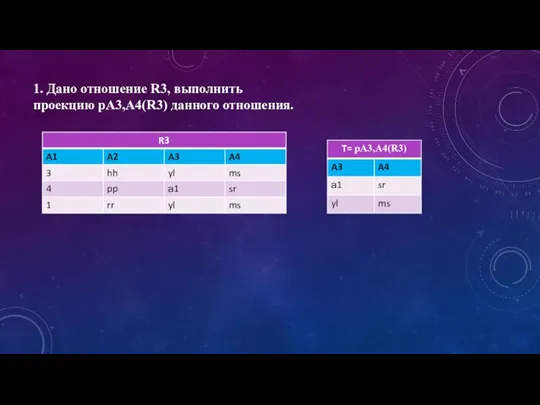 Дано отношение R3, выполнить проекцию pA3,A4(R3) данного отношения
Дано отношение R3, выполнить проекцию pA3,A4(R3) данного отношения Методы и приемы решения дробно-рациональных уравнений, содержащих параметр
Методы и приемы решения дробно-рациональных уравнений, содержащих параметр Переход от передаточных функций к дифференциальным уравнениям и структурным схемам
Переход от передаточных функций к дифференциальным уравнениям и структурным схемам Площадь круга. Геометрическая сказка. 6 класс
Площадь круга. Геометрическая сказка. 6 класс Тригонометрические функции. Формулы двойного угла
Тригонометрические функции. Формулы двойного угла Решение задач. Пирамида
Решение задач. Пирамида Прямоугольный параллелепипед. Многогранники
Прямоугольный параллелепипед. Многогранники Аксиомы стереометрии
Аксиомы стереометрии Случаи сложения вида +6
Случаи сложения вида +6 Десятичные дроби
Десятичные дроби Задачи на соответствие графиков формулам их задающим
Задачи на соответствие графиков формулам их задающим Иррациональные уравнения
Иррациональные уравнения Золотое сечение
Золотое сечение Пирамида, её основание, вершина, боковые рёбра, высота, боковая поверхность
Пирамида, её основание, вершина, боковые рёбра, высота, боковая поверхность Роль дистанционных конкурсов по математике в гуманитарном развитии обучающихся
Роль дистанционных конкурсов по математике в гуманитарном развитии обучающихся Решение задач. Подготовка к умножению
Решение задач. Подготовка к умножению Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже
Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже Морское путешествие
Морское путешествие Устный счёт Прицепи вагоны. 2 класс
Устный счёт Прицепи вагоны. 2 класс Обратные задакчи
Обратные задакчи Отношения и пропорции. Повторение
Отношения и пропорции. Повторение Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Úsh perpendıkýlıar týraly teorema
Úsh perpendıkýlıar týraly teorema