Определение производной

Задача о вычислении мгновенной скорости
s ( t ) = 4 t² - закон движения материальной точки по прямой
s - путь, пройденный за время t (t ≥ 0)
Вычислим v ср - среднюю скорость точки за промежуток времени от t 1 = 2 до t 2 = 5
s (2) =
4 · 2² =
16;
s (5) =
4 · 5² =
100;
s (5) ̶ s (2) =
100 – 16 = 84;
t 2 - t 1 =
5 – 2.

Пусть точка движется вдоль прямой по закону S(t).
Тогда за промежуток времени t точка проходит расстояние S(t).
Пусть ∆t – малый промежуток времени. Путь, пройденный за время t+ ∆t, равен S(t+ ∆t ).
Тогда средняя скорость
∆t
t0
t
t+∆t

Задача о вычислении мгновенной скорости
s ( t ) = 4 t ²
Вычислим v ср
s (t) = 4 t ²;
s (t + Δ t) =
4 (t + Δ t)² ;
Δ s = s (t + Δ t) ̶ s (t) – путь, пройденный точкой за промежуток времени от t до t + Δ t
за промежуток времени от t до t + Δ t
Δ s = 4 (t + Δ t)² - 4 t ² =
(8 t + 4Δ t) Δ t ;

Общий случай:
точка движется по прямой по закону s(t) = f (t)
Тогда её мгновенной скоростью v в момент времени t называют предел (если он существует), к которому стремится её средняя скорость на промежутке времени [t; t + Δt] при Δ t → 0 :
Величина Δ t – приращение времени
Величина Δ f = f(t + Δt) – f(t) - приращение пути

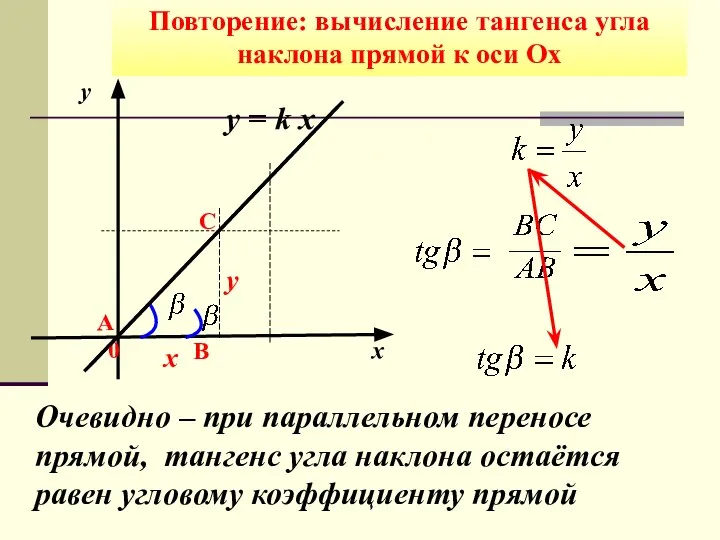
В
у
х
0
Повторение: вычисление тангенса угла наклона прямой к оси Ох
А
С
y = k x
у
х
Очевидно – при параллельном переносе прямой, тангенс угла наклона остаётся равен угловому коэффициенту прямой

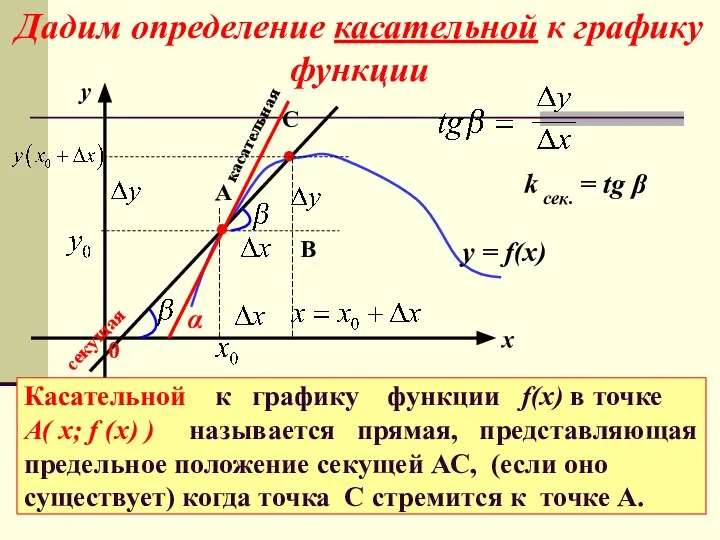
у = f(x)
С
●
В
касательная
Касательной к графику функции f(x) в точке
А( х; f (х) ) называется прямая, представляющая предельное положение секущей АС, (если оно существует) когда точка С стремится к точке А.
секущая
у
х
0
Дадим определение касательной к графику функции
A
●
α
k сек. = tg β

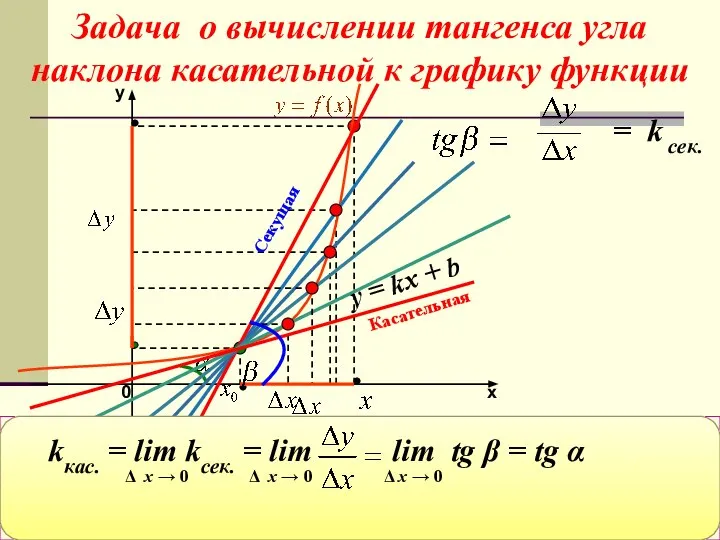
Секущая стремится занять положение касательной.
То есть, касательная есть предельное положение секущей.
Секущая
Задача о вычислении тангенса угла наклона касательной к графику функции
При Δ х → 0 угловой коэффициент секущей (kсек. ) стремится к угловому коэффициенту касательной (kкас. )
y = kx + b

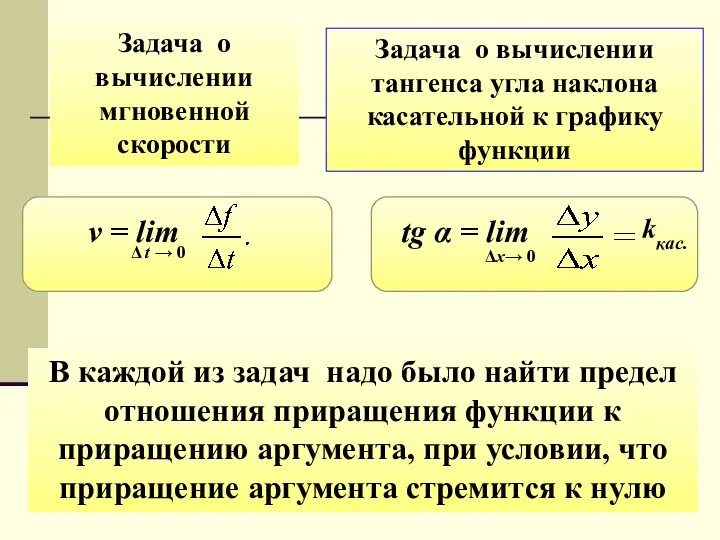
Задача о вычислении мгновенной скорости
Задача о вычислении тангенса угла наклона касательной к графику функции
kкас.
В каждой из задач надо было найти предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента стремится к нулю

Историческая справка

Тайны планетных орбит.
Древнегреческие учёные умели решать немногие задачи кинематики – рассчитать либо равномерное прямолинейное движение, либо равномерное вращение вокруг оси.
А планеты на небосводе двигались по самым замысловатым кривым . Свести эти движения планет к простым древним учёным не удавалось.
Лишь в 17 веке немецкому учёному Иоганну Кеплеру удалось сформулировать законы движения планет. Оказалось, что планеты движутся по эллипсам, и притом неравномерно. Объяснить, почему это так, Кеплер не смог.

В конце 17 века Исаак Ньютон открыл законы динамики, сформулировал закон всемирного тяготения и развил математические методы, позволявшие сводить неравномерное к равномерному, неоднородное к однородному, криволинейное к прямолинейному.
В основе лежала простая идея – движение любого тела за малый промежуток времени можно приближённо рассматривать как прямолинейное и равномерное.
Одновременно с Ньютоном немецкий философ и математик Готфрид Вильгельм Лейбниц изучал, как проводить касательные к произвольным кривым.

Он также развил новое исчисление, которое оказалось по сути дела тождественным построенному Ньютоном. Обозначения, введённые Лейбницем, оказались настолько удачными, что сохранились и по сей день.
Новая математика Ньютона и Лейбница состояла из двух больших частей – дифференциального и интегрального исчислений.
В первом из них говорилось, как, изучая малую часть явления, сводить неравномерное к равномерному.
Во второй – как из малых равномерных частей конструировать сложное неравномерное явление.

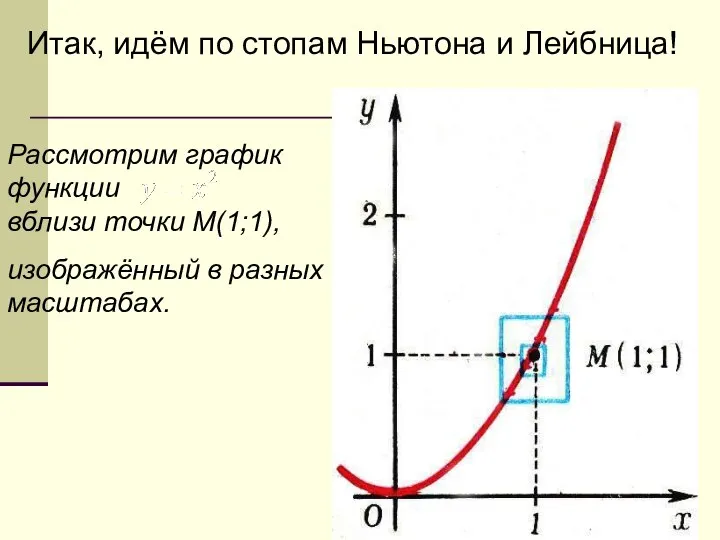
Итак, идём по стопам Ньютона и Лейбница!
Рассмотрим график функции вблизи точки М(1;1),
изображённый в разных масштабах.

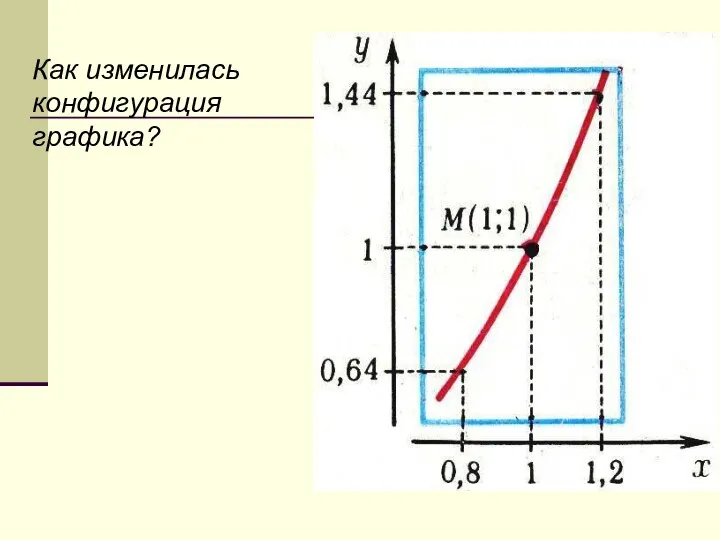
Как изменилась конфигурация графика?

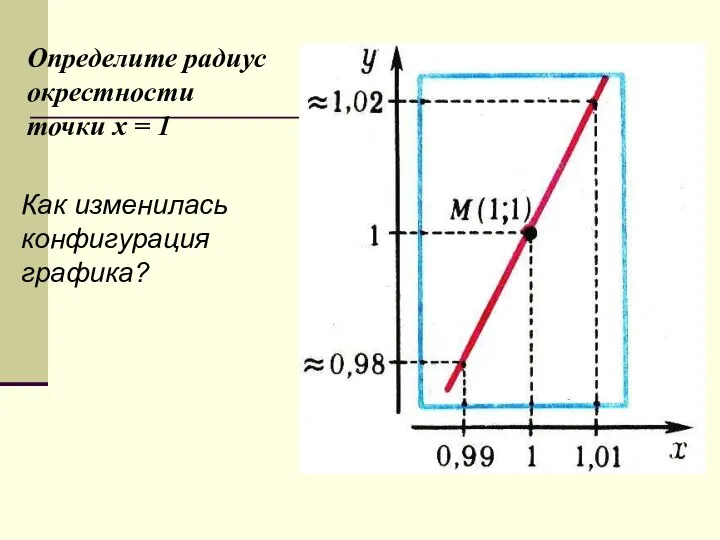
Определите радиус окрестности точки х = 1
Как изменилась конфигурация графика?

Основные выводы
1. Чем крупнее масштаб, тем меньше график функции будет отличаться от некоторой прямой, проходящей через точку М(1;1).
2. То же самое будет происходить с графиком функции вблизи любой другой точки.
3. Этим свойством обладают и многие другие кривые: окружность, гипербола, синусоида и т. д.
Такое свойство функций называют «линейность в малом»

Очевидно, если ∆t 0, то Vср. Vмгн.
Значит,

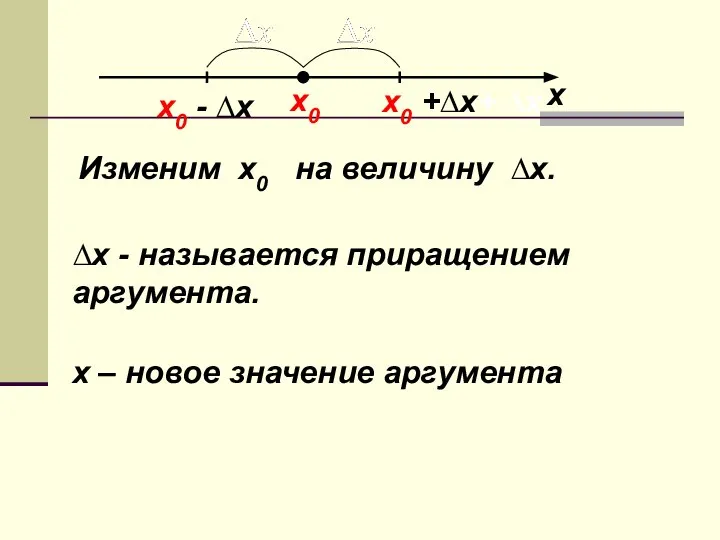
х
х0
Изменим x0 на величину ∆x.
∆x - называется приращением аргумента.
x0 +∆x+ ∆x
x0 - ∆x
x – новое значение аргумента

Величина y(x) – y(x0) называется приращением функции в точке x0 и обозначается ∆y(x0) .

Таким образом, чтобы вычислить приращение функции f(x) при переходе от точки x0 к точке x = x0 + Δx , нужно:
1. найти значение функции f(x0);
2. найти значение функции f(x0 + Δx)
3. найти разность f(x0 + Δx) – f(x0)

В математике операция нахождения предела отношения приращения функции Δ f к приращению аргумента Δ x , при условии, что приращение Δ x → 0 называется -
дифференцирование функции
Результат выполнения называют
производной
и обозначают:

Определение производной

Определение производной

Чтобы найти производную функции в точке, надо:
найти приращение функции в точке Х0 ;
найти отношение приращения функции к приращению аргумента;
вычислить предел полученного отношения при условии, что приращение аргумента стремится к нулю.

Пример нахождения производной
Решение

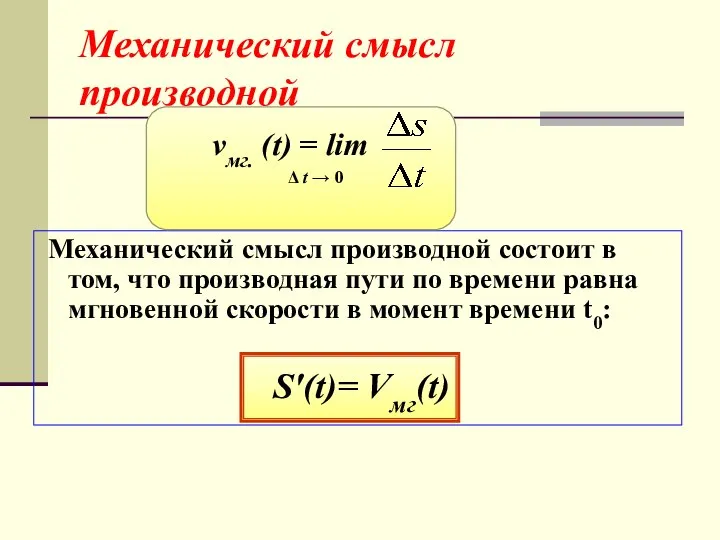
Механический смысл производной
Механический смысл производной состоит в том, что производная пути по времени равна мгновенной скорости в момент времени t0:
S'(t)= Vмг(t)