Слайд 2Термины и определения
Неопределенность измерения – параметр, связанный с результатом измерения и характеризующий

разброс значений, которые с определенной вероятностью могут быть приписаны определяемой величине
Результат измерений - значение характеристики, полученное выполнением регламентированного метода измерения
Погрешность измерения –отклонение измеренного значения от истинного содержания определяемого компонента
Доверительная вероятность – вероятность появления случайной ошибки. Показывает, какое число опытов из 100 дают правильные результаты в пределах заданной точности
Дисперсия – рассеяние результатов относительно среднего значения
Доверительный интервал – значения, в пределах которых может заключаться истинное значение определяемой величины
Слайд 3Классификация погрешностей
По способу вычисления погрешности
По влиянию на результат анализа
По характеру причин, их
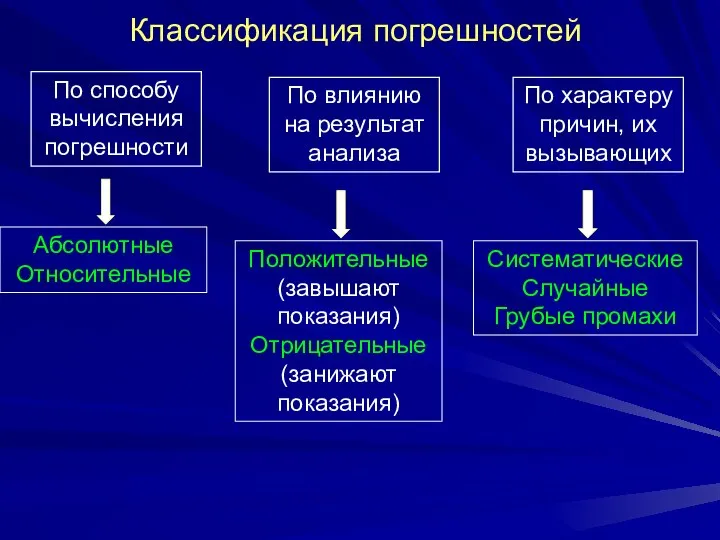
вызывающих
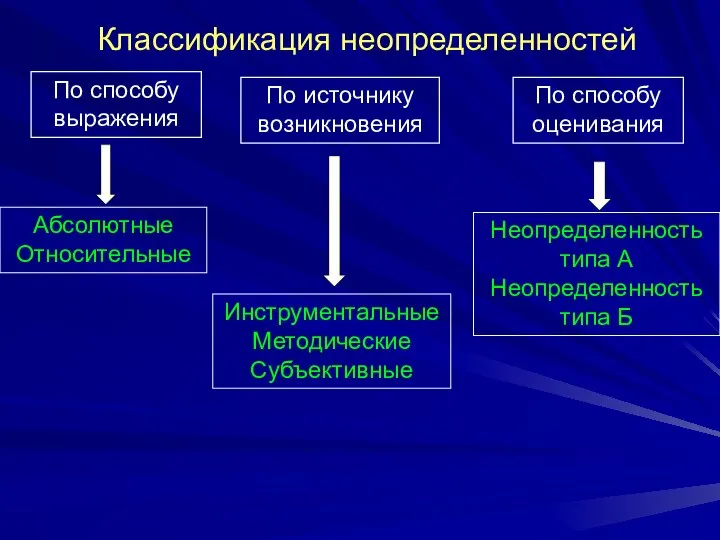
Слайд 4Классификация неопределенностей
По способу выражения
По источнику возникновения
По способу оценивания
Слайд 5Аналоги концепции неопределенности и классической теории точности

Слайд 6Порядок обработки данных
1. Порядок обработки выборочной совокупности
1. Проводят исследования в соответствии

с МВИ и получают 5-10 результатов измерений
2. Располагают результаты в порядке возрастания
3. Для каждого результата рассчитывают Q-критерий по формуле
Q эксп=(Х+- Хi)/(Хmax- Хmin)
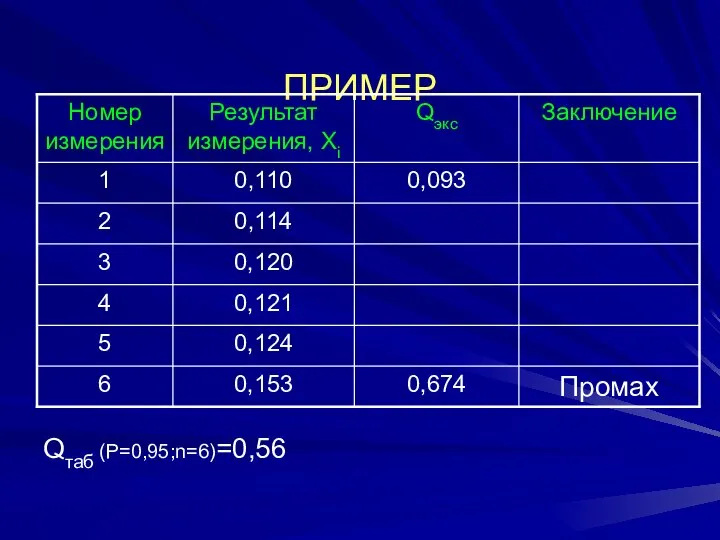
4. Сравнивают полученные значения с табличным значением Q таб
5. Результаты, для которых Q эксп больше Q таб, из дальнейших расчетов исключают
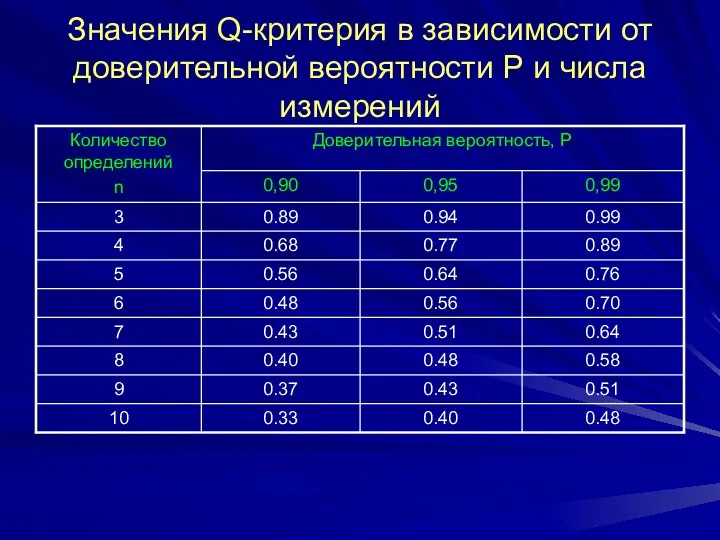
Слайд 7Значения Q-критерия в зависимости от доверительной вероятности Р и числа измерений
Слайд 8Алгоритм расчета неопределенности
Рассчитывают среднее значение для оставшихся результатов, полученных по п.5

Рассчитывают стандартную неопределенность по типу А
Рассчитывают доверительный интервал при Р=0,95
Рассчитывают стандартную неопределенность по типу Б
Рассчитывают суммарную стандартную неопределенность
Рассчитывают расширенную неопределенность
Представляют результат измерения в виде:
Х = Хср ± U
Слайд 9Формулы для расчета
Среднее значение
Стандартная неопределенности по типу А
Доверительный интервал при Р=0,95

Слайд 10Стандартная неопределенность по типу Б (при симметричном распределении)
Суммарная стандартная неопределенность
Расширенная неопределенность при

Р=0,95
Слайд 11Правила представления результата
Правило 1
Неопределенность указывают двумя значащими цифрами, если первая из

них равна 1 или 2, и одной – если первая цифра 3 и более
Правильно: 12,0 ± 0,4; 0,088 ± 0,018
Неправильно:12,00 ± 0,40; 0,0877 ± 0,0183
Слайд 12Правило 2 (равенства разрядов)
Наименьший разряд числового значения результата должен совпадать с

наименьшим разрядом числового значения неопределенности измерения
Правильно: 12,0 ± 0,4;
675 ± 25; 0,15 ± 0,03
Неправильно: 12 ± 0,4;
675,0 ± 25,2 0,15 ± 0,031
Слайд 14Число измерений – 5
Среднее значение – 0,119
Стандартная неопределенность по типу А –

0,0065
Доверительный интервал – 0,0074
Стандартна неопределенность по типу Б - 0,004
Суммарная стандартная неопределенность – 0,005
Расширенная неопределенность – 0,010
Полученный результат:
0,119 ± 0,010
(Правильно ли записан результат?)
Слайд 15Список литературы
ГОСТ Р ИСО 5725-1-2002 «Точность (правильность и прецизионность) методов и результатов

измерений. Часть 1. Основные положения и определения»;
ГОСТ Р ИСО 5725-2-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений»;
ГОСТ Р ИСО 5725-3-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений»;
Слайд 16ГОСТ Р ИСО 5725-4-2002 «Точность (правильность и прецизионность) методов и результатов измерений.

Часть 4. Основные методы определения правильности стандартного метода измерений»;
ГОСТ Р ИСО 5725-5-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений»;
ГОСТ Р ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике».














 Домашнее задание. Решение задач
Домашнее задание. Решение задач Векторы на плоскости
Векторы на плоскости Случаи вычитания 11-
Случаи вычитания 11- Знакомство с основными понятиями в математике. Задачи с несколькими вопросами
Знакомство с основными понятиями в математике. Задачи с несколькими вопросами Древнекитайское доказательство
Древнекитайское доказательство Пределы
Пределы История теоремы Пифагора
История теоремы Пифагора Построение сечений многогранников
Построение сечений многогранников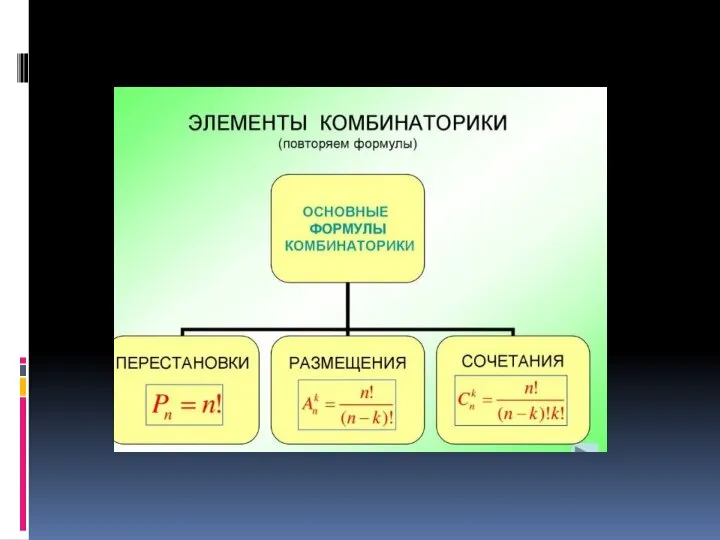 Основные понятия комбинаторики
Основные понятия комбинаторики предел_числ_посл
предел_числ_посл Стереометрия. Многогранники
Стереометрия. Многогранники Отношения и пропорции. Золотое сечение
Отношения и пропорции. Золотое сечение Площади и объемы
Площади и объемы Частные производные. Полный дифференциал функции
Частные производные. Полный дифференциал функции Многоугольники
Многоугольники Многочлены с несколькими переменными и их стандартный вид
Многочлены с несколькими переменными и их стандартный вид Кусочная функция
Кусочная функция Символика и терминология. Системы координат. Лекция 1
Символика и терминология. Системы координат. Лекция 1 Презентация на тему Слагаемое сумма
Презентация на тему Слагаемое сумма  Чётность и не чётность тригонометрических функций
Чётность и не чётность тригонометрических функций Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Презентация на тему Нумерация в пределах 1000
Презентация на тему Нумерация в пределах 1000  Призма. Понятие и чертёж
Призма. Понятие и чертёж 1_2_opredeliteli (1)
1_2_opredeliteli (1) Центральная симметрия
Центральная симметрия Домашнее задание . Подготовка к контрольной работе
Домашнее задание . Подготовка к контрольной работе Решение задач на кратное сравнение чисел
Решение задач на кратное сравнение чисел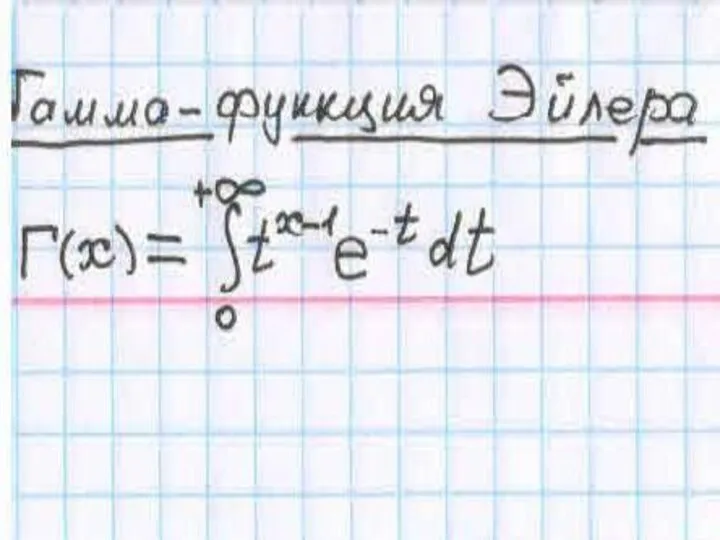 Гамма-функция Эйлера
Гамма-функция Эйлера