Содержание
- 2. Устный счет
- 3. 3+2=5 3 – ПЕРВОЕ СЛАГАЕМОЕ 2 – ПЕРВОЕ СЛАГАЕМОЕ сумма 5 – ЗНАЧЕНИЕ СУММЫ
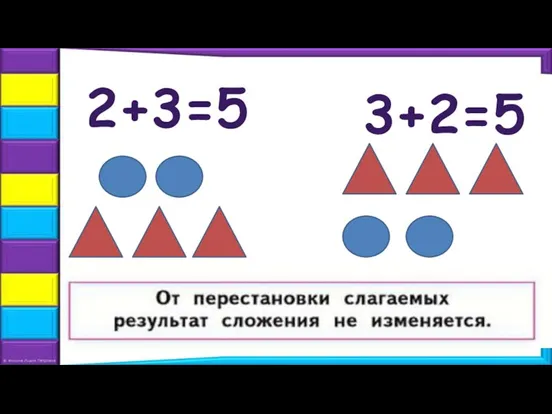
- 4. 2+3=5 3+2=5
- 5. 5-2=3 5 – УМЕНЬШАЕМОЕ 2 – ВЫЧИТАЕМОЕ разность 3 – ЗНАЧЕНИЕ РАЗНОСТИ
- 6. Мы гостей позвать решили, И друзей всех обзвонили: Мама - двух своих подруг, Папа - двух
- 7. Мы гостей позвать решили, И друзей всех обзвонили: Мама - двух своих подруг, Папа - двух
- 8. Кузьмы в руках корзина, В ней лежат две апельсина, Шесть слив и две хурмы. Сколько фруктов
- 9. Кузьмы в руках корзина, В ней лежат две апельсина, Шесть слив и две хурмы. Сколько фруктов
- 10. На лужайке у реки Расселились мотыльки: 2 сидели на ромашках, 8 -на душистых кашках, Да 1
- 11. На лужайке у реки Расселились мотыльки: 2 сидели на ромашках, 8 -на душистых кашках, Да 1
- 12. 15 февраля. 5 5 5 5 5
- 13. СТР.31
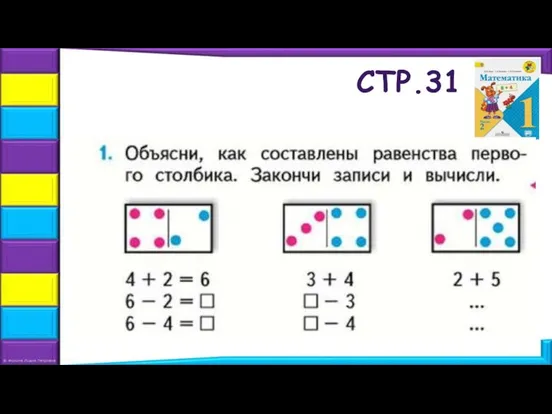
- 14. ЦЕЛЬ НА УРОК: СТР.31 Продолжим изучать связь Между суммой и каждым слагаемым. Решаем задачи.
- 15. СТР.31
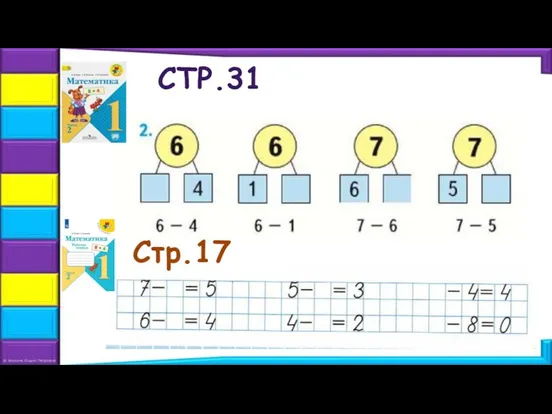
- 16. СТР.31 Стр.17
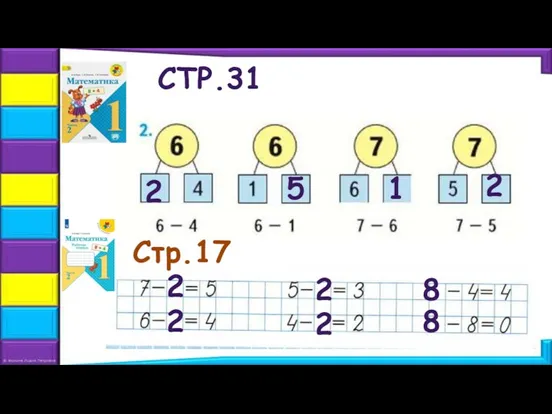
- 17. СТР.31 Стр.17 2 5 1 2 2 2 2 2 8 8
- 18. СТР.31
- 19. СТР.31 6-2= 4 6+4= 10
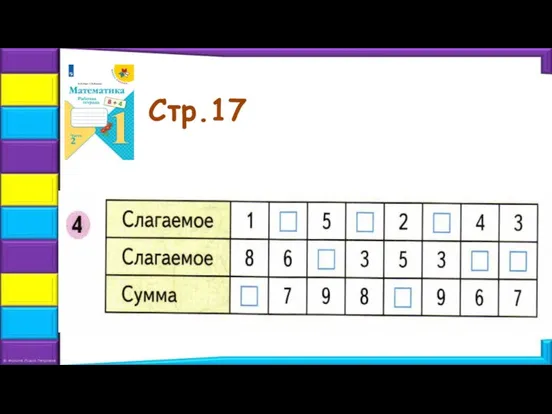
- 22. Стр.17
- 24. Скачать презентацию














 Решение уравнений с модулем
Решение уравнений с модулем Презентация на тему Построение диаграмм и графиков функций
Презентация на тему Построение диаграмм и графиков функций  Формулы. Уравнение
Формулы. Уравнение Правильные многогранники. Формула Эйлера. Правильные многогранники в философской картине мира Платона. Кубок Кеплера
Правильные многогранники. Формула Эйлера. Правильные многогранники в философской картине мира Платона. Кубок Кеплера Самостоятельная работа к урокам 31-34
Самостоятельная работа к урокам 31-34 Способы построения параллельных прямых
Способы построения параллельных прямых Статистика. Статистические дисциплины
Статистика. Статистические дисциплины Единицы измерения длины
Единицы измерения длины Квадратный корень из степени
Квадратный корень из степени Решение уравнений и неравенств с модулем
Решение уравнений и неравенств с модулем Решение задач. Параллельные прямые
Решение задач. Параллельные прямые Римские цифры
Римские цифры Сфера. Окружность и круг
Сфера. Окружность и круг Одиниці вимірювання часу
Одиниці вимірювання часу Замена переменных в определенном интеграле. Лекция 4
Замена переменных в определенном интеграле. Лекция 4 Терема Пифагора
Терема Пифагора Первообразная и интеграл
Первообразная и интеграл Фигуры. Геометрия
Фигуры. Геометрия Математику нельзя изучать, наблюдая, как это делает сосед (задачи)
Математику нельзя изучать, наблюдая, как это делает сосед (задачи) Построение сечений многогранников
Построение сечений многогранников Тренажёр Единицы измерени времени
Тренажёр Единицы измерени времени Свидетели истории народа
Свидетели истории народа Деление с остатком
Деление с остатком Все способы решения тригонометрических уравнений
Все способы решения тригонометрических уравнений Многозначная логика
Многозначная логика Циліндр. Елементи циліндра
Циліндр. Елементи циліндра Разложение многочлена на множители
Разложение многочлена на множители Тупиковая ДНФ. Метод Блейка-Порецкого
Тупиковая ДНФ. Метод Блейка-Порецкого