Элементы комбинаторики

Комбинаторика – это раздел
математики, в котором изучаются
вопросы выбора или расположения элементов множества в
соответствии с заданными правилами.
Т.е. в комбинаторике изучаются задачи, связанные с рассмотрением конечных множеств и составлением различных комбинаций из элементов этих множеств.
1. Основные понятия комбинаторики

Пример 1.
Из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 можно составить следующие комбинации чисел: 123, 321, 312, 213, 516, 59, 4901…
Т.о., полученные комбинации удовлетворяют различным условиям.
В зависимости от правил составления можно выделить 3 типа комбинаций:
перестановки;
размещения;
сочетания.

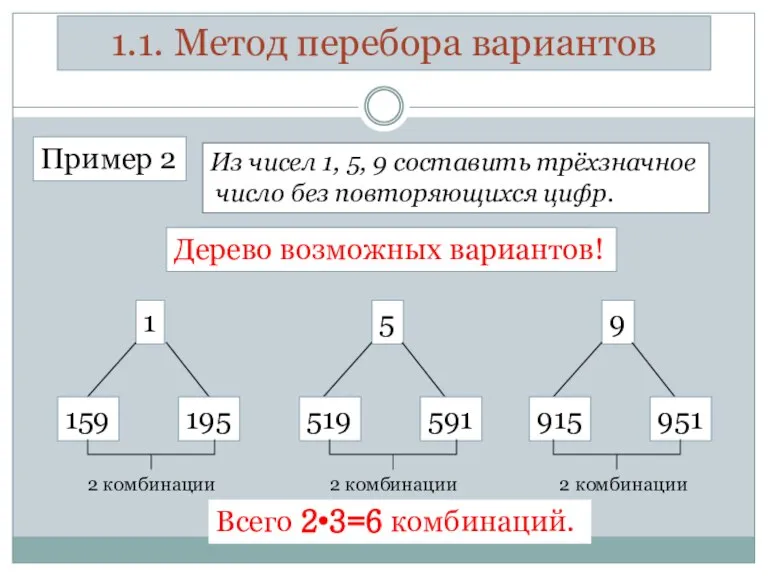
1.1. Метод перебора вариантов
Пример 2
Из чисел 1, 5, 9 составить трёхзначное
число без повторяющихся цифр.
Организованный перебор!
1
159
195
5
9
519
591
915
951
2 комбинации
2 комбинации
2 комбинации
Всего 2•3=6 комбинаций.
Дерево возможных вариантов!

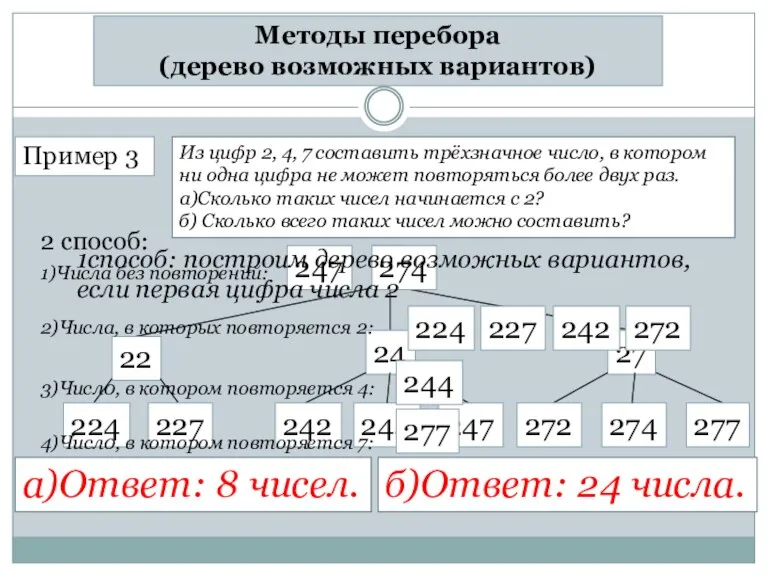
Методы перебора
(дерево возможных вариантов)
Пример 3
Из цифр 2, 4, 7 составить трёхзначное число, в котором
ни одна цифра не может повторяться более двух раз.
а)Сколько таких чисел начинается с 2?
б) Сколько всего таких чисел можно составить?
2
24
22
27
224
227
242
247
272
277
274
244
а)Ответ: 8 чисел.
б)Ответ: 24 числа.
1)Числа без повторений:
247
274
2)Числа, в которых повторяется 2:
224
227
242
272
3)Числ0, в котором повторяется 4:
244
4)Числ0, в котором повторяется 7:
277
1способ: построим дерево возможных вариантов,
если первая цифра числа 2
2 способ:

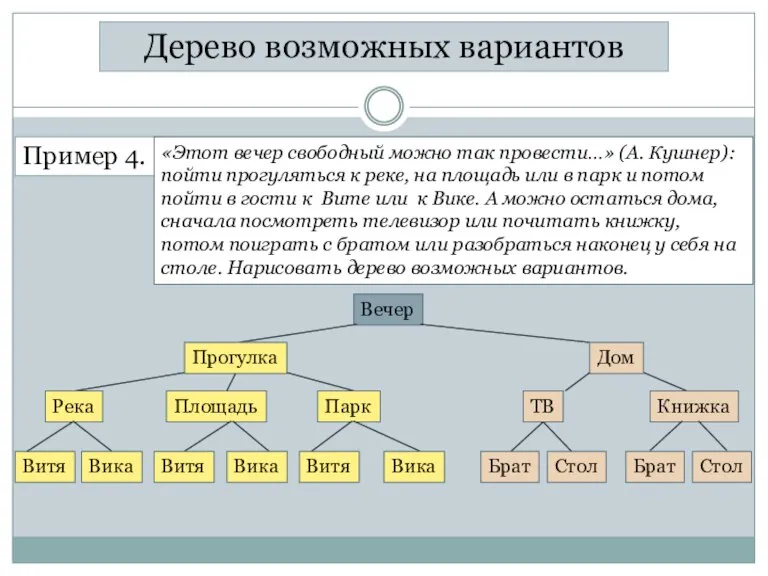
Дерево возможных вариантов
Пример 4.
«Этот вечер свободный можно так провести…» (А. Кушнер):
пойти прогуляться к реке, на площадь или в парк и потом пойти в гости к Вите или к Вике. А можно остаться дома,
сначала посмотреть телевизор или почитать книжку, потом поиграть с братом или разобраться наконец у себя на столе. Нарисовать дерево возможных вариантов.
Вечер
Прогулка
Дом
Парк
Площадь
Река
Витя
Вика
Витя
Витя
Вика
Вика
ТВ
Книжка
Брат
Стол
Брат
Стол

На завтрак можно выбрать булочку, кекс, пряники или печенье, запить можно чаем, соком или кефиром. Сколько вариантов завтрака есть?
х/б
изд.
напитки
булочка
кекс
пряники
печенье
чай
сок
кефир
чай
чай
чай
чай
кефир
сок
сок
сок
сок
кефир
кефир
кефир
булочка
булочка
булочка
кекс
кекс
кекс
пряники
пряники
пряники
печенье
печенье
печенье
Выбор напитка- испытание А
Выбор хл./бул. изделия.- испытание В
Испытание А имеет 3 варианта (исхода), а испытание В-4, всего вариантов
независимых испытаний А и В 3•4=12.
Для того, чтобы найти число
всех возможных исходов
(вариантов) независимого
проведения двух испытаний
А и В, надо перемножить число
всех исходов испытания А на
число всех исходов испытания В
1.2. Правило умножения (произведения)

Пример 5. Сколько различных двузначных чисел можно записать с помощью цифр 0, 1, 2, 3?
Решение.
В качестве первой цифры может быть выбрана любая из цифр 1, 2, 3, т.е. п=3.
Второй цифрой может быть выбрана любая из четырех данных цифр 0, 1, 2, 3, т.е. т = 4.
Согласно правилу произведения число всевозможных двузначных чисел, составленных с помощью предложенных цифр, равно
п*т = 3*4=12.
Ответ: 12.

Семейный ужин.
Пример 6.
В семье 6 человек, а за столом в кухне 6 стульев. Было решено каждый вечер перед ужином рассаживаться на эти 6 стульев по-новому. Сколько дней члены семьи смогут делать
это без повторений?
№1
№2
№3
№4
№5
№6
6
5
4
3
2
1
6•5•4•3•2•1=
720дн.
-почти 2 года

1.3. Понятие факториала
Произведение всех натуральных чисел от 1 до п включительно называют
п-факториал и обозначают:
n! = 1•2•3•…•(n-1)•n.
Удобные формулы:
n!=(n-1)!•n
(n+1)!=п!•(n+1)
0! = 1
1! = 1
2! = 1•2 = 2
3! = 1•2•3 = 6
4! = 1•2•3•4 = 3!•4 = 24
5! = 1•2•3•4•5 = 4!•5 = 24•5 = 120
6! = 1•2•3•4•5•6 = 5!•6 = 120•6 = 720
7! = 1•2•3•4•5•6•7 = 6!•7 = 720•7 = 5040

Пример 7.

Пример 8.
Сколькими способами 4 вора могут по одному разбежаться на все 4 стороны.
2
1
3
4
N
O
W
S
Банк
4
3
2
1
1•2•3•4=4!=24
Их разыскивает полиция…

Расписание уроков.
Пример 9.
В 9 классе в среду 7 уроков: алгебра, геометрия, литература,
русский язык, английский язык, биология и физкультура.
Сколько вариантов расписания можно составить?
Расставляем предметы по порядку
Алгебра
7
Геометрия
6
Литература
5
Русский язык
4
Английский язык
3
Биология
2
1
Физкультура
Всего вариантов расписания
1•2•3•4•5•6•7=
=5040
7!=

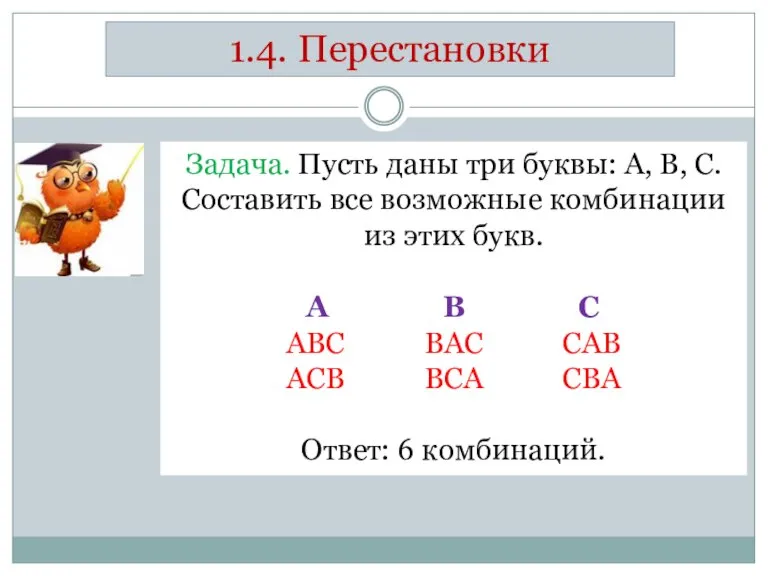
1.4. Перестановки
Задача. Пусть даны три буквы: А, В, С. Составить все возможные комбинации из этих букв.
А В С
АВС ВАС САВ
АСВ ВСА СВА
Ответ: 6 комбинаций.

1.4. Перестановки
Перестановками из п элементов называются соединения, которые состоят из одних и тех же n элементов и отличаются одно от другого только порядком их расположения.
Комбинации из п элементов, которые отличаются друг от друга только порядком элементов называются перестановками.
Число перестановок из п элементов обозначают Рп и читают «пэ энное»

Задача
Сколькими способами можно поставить рядом на полке 4 различные книги?
Решение. На первое место можно поставить любую из четырех книг, на второе – любую из трех оставшихся книг, на третье – любую из двух оставшихся книг и на четвертое место – последнюю оставшуюся книгу.
Применяя формулу Р4 = 4·3·2·1=24
Ответ: книги можно поставить 24 способами.

Задача
Сколькими способами можно положить 6 различных открыток в 6 имеющихся конвертов (по одной открытке в конверт)?
Решение. Задача сводится к нахождению числа перестановок из 6 элементов.
Применяя формулу, получим
Р6 = 6! = 1·2·3·4·5·6 = 720
Ответ: 720 способами.

Пример.
Даны три числа 1, 5, 9. Посчитать число перестановок.
Решение. Р3 = 3!=6
159, 195, 519, 591, 915, 951.
Ответ: 6 комбинаций.

Пример. Даны числа 1, 2, 3, 4. Посчитать и записать число перестановок.
Решение. Р4 = 4!= 24
1 2 3 4
1234 2134 3124 4123
1243 2143 3142 4132
1324 2413 3241 4231
1342 2431 3214 4213
1423 2314 3314 4312
1432 2341 3341 4321
Ответ: 24 комбинации.

Задание.

1.5. Размещения
Задача.
Сколько различных двузначных чисел можно составить с помощью цифр 1, 2, 3, 4 при условии, что в каждой записи нет одинаковых цифр?
Решение. Перебором убедимся в том, что из четырех цифр 1, 2, 3, 4 можно составить 12 двузначных чисел, удовлетворяющих условию:
12, 13, 14,
21, 23, 24,
31, 32, 34,
41, 42, 43.
В записи двузначного числа на первом месте может стоять любая из данных четырех цифр, а на втором – любая из оставшихся. По правилу произведения таких двузначных чисел 4*3=12. Ответ: 12.

1.5. Размещения
Размещениями из т элементов по п элементов (п≤т) называются такие соединения, каждое из которых содержит п элементов, взятых из данных т разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения.
Число размещений из т элементов по п элементов обозначают и читают «А из эм по эн»

Примеры.
Т.е. число размещений из п элементов по п равно числу перестановок из этих элементов.

Формула для нахождения числа размещений

Задания.
Сколько существует вариантов распределения трех призовых мест, если в розыгрыше участвуют 7 команд?
Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, …, 9?
Сколько вариантов расписания можно составить на один день, если всего имеется 8 учебных предметов, а в расписание на день могут быть включены только 3 из них?
Сколько вариантов распределения трех путевок в санатории различного профиля можно составить для пяти претендентов?
Ответы: 210; 5040; 336; 60.

Задания.
Сколько существует способов для обозначения с помощью букв A, B, C, D, E, F вершин данного треугольника? (ответ: 120)
В группе 20 человек. Сколькими способами из их числа можно сделать назначение: физорга и культорга? Физорга, культорга и казначея? (6840)
Найти значение выражения:

1.5. Сочетания и их свойства
Сочетаниями из т элементов по п в каждом (n≤m) называются соединения, каждое из которых содержит n элементов, взятых из данных т разных элементов, и которые отличаются одно от другого по крайней мере одним элементом.
Число всевозможных сочетаний из т различных элементов по п элементов обозначают и читают «С из эм по эн»

Задача. Сколько существует способов выбора двух карт из колоды в 36 карт?
Изымаемые из колоды всевозможные пары карт без учета порядка их расположения в наборе образуют сочетания из 36 по 2. По формуле (2) находим:

Свойства сочетаний

Задания.

Задачи.
Сколькими способами для участия в конференции из 9 членов научного общества можно выбрать четверых студентов? (126)
Сколько различных аккордов, содержащих 3 звука, можно образовать из 12 клавиш одной октавы? (220)
В помещении 16 ламп. Сколько существует вариантов его освещения, если одновременно должны светиться 14 ламп? (120)
На окружности отмечено 12 точек. Сколько различных треугольников с вершинами в этих точках можно построить? (220)

2. Формула бинома Ньютона
В теории многочленов часто двучлены называют биномами.
Рассмотрим целые неотрицательные степени бинома (a+b) (при условии a+b≠0):

Формула бинома Ньютона для натуральных m имеет вид
где числа
- биномиальные коэффициенты, которые легко находить из треугольника Паскаля.

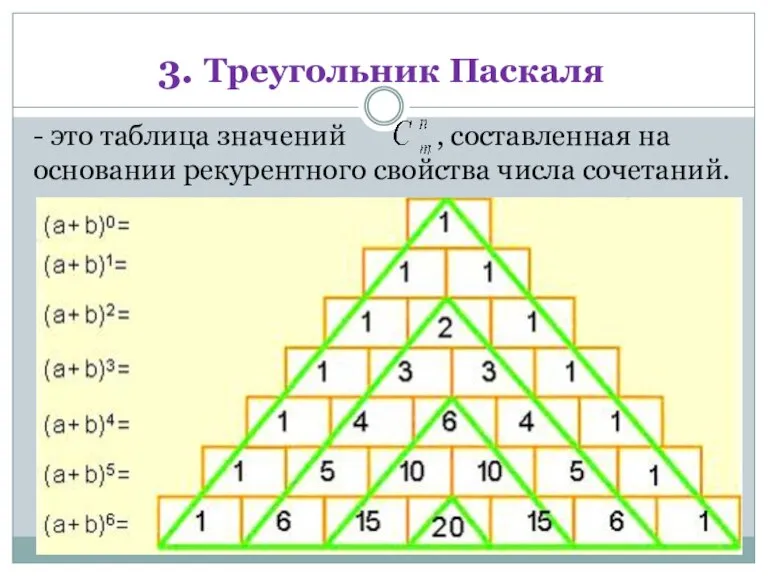
3. Треугольник Паскаля
- это таблица значений , составленная на основании рекурентного свойства числа сочетаний.

Свойства биномиальных коэффициентов
Для коэффициентов бинома Ньютона справедливы следующие свойства:
1) коэффициенты, равноудаленные от начала и конца разложения, равны между собой
где p=0,1,2,…,n;
2)
3) сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома Ньютона:
сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.

Пример. Записать разложение бинома