Дискретная математика. Повторение арифметических действий

Повторение арифметических действий
A16
1С52
891
+
3
E
20
16
-
4
1
2

5354
Вычитание в системах счисления
A8
6354
703
-
1
5
8
11
-
7
5
4

Умножение в системах счисления
A16
20А4
В15
×
20=
1
×16+
4
51=
3
×16+
3
3 =
3
10 =
А
4
A
0
2
44=
2
×16+
C
112=
7
×16+
0
7=
7
22=
1
×16+
6
1
169B974

Деление в системах счисления
A2
10101
11
1
11
-
10
0
1
-
11
1
1
1
11
0
Самостоятельно: 1101112 / 1012 =
10112

Деление в системах счисления
A8
46230
53
7
455
-
5
3
1
-
53
0
0
0
Самостоятельно: 4048 / 248 =
158
53
×
7
Подбор
5
2
45
53
×
5
7
1
32
53
×
6
2
2
40

Деление в системах счисления
A16
4C98
2B
1
2B
-
21
9
C
-
204
15
8
8
Самостоятельно:
165016 / 1516 =
11016
2B
×
2
Подбор
6
1
5
2B
×
A
E
6
1A
2B
×
C
4
8
20
158
-
0

Пожалуйста, пройдите
Тестирование на деление
Для его выполнения
Создайте отдельную вкладку в браузере чтобы не «потерять» трансляцию

Арифметические действия (повтор)
5357 + 16247 =
?9
759 - 73869 =
92610
?10
?2
?16
-73119
AB16 × 4316 =
2CC116
101101102 / 1112 =
110102

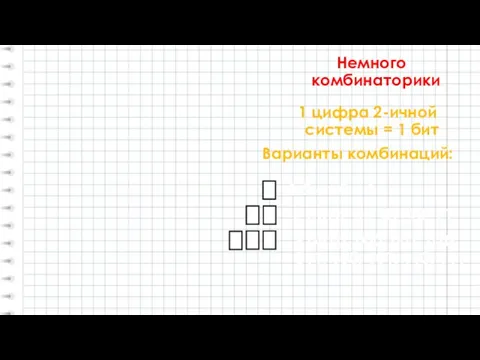
Немного комбинаторики
1 цифра 2-ичной системы = 1 бит
1 бит: 0 и 1
Варианты комбинаций:
2 бита: 00; 01; 10; 11
3 бита: 000; 001; 010; 011; 100; 101; 110; 111

Немного комбинаторики
Итак, сколько различных чисел можно написать?
2=21
4=22
8=23
16=24
?
64=26
Степенносвязанные
Системы счисления

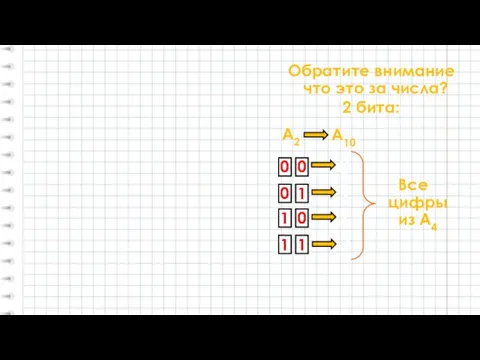
Обратите внимание что это за числа?
0
0
2 бита:
0
1
1
0
1
1
A2
A10
0
1
2
3
Все цифры из A4

Вывод: Каждые ДВЕ цифры двоичной системы можно записать соответствующей цифрой 4-ичной системы

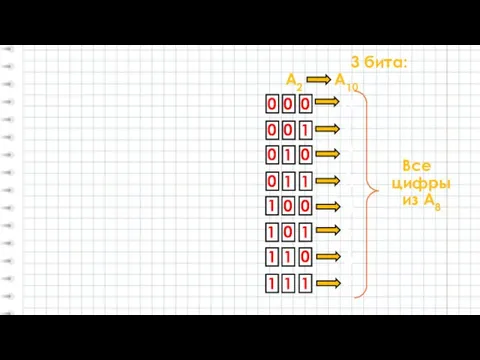
0
0
3 бита:
0
1
1
0
1
1
A2
A10
0
1
2
3
Все цифры из A8
0
0
0
1
1
0
1
1
0
0
0
0
1
1
1
1
4
5
6
7

Вывод: Каждые ТРИ цифры двоичной системы можно записать соответствующей цифрой 8-ичной системы

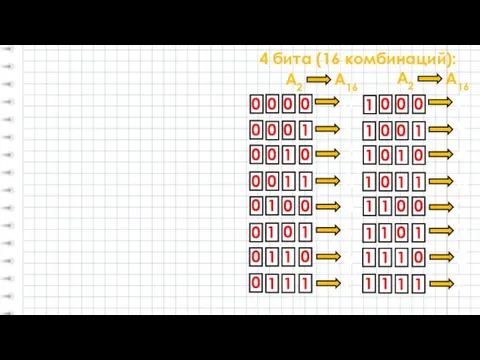
0
0
4 бита (16 комбинаций):
0
1
1
0
1
1
A2
A16
0
1
2
3
0
0
0
1
1
0
1
1
0
0
0
0
1
1
1
1
4
5
6
7
0
0
0
0
0
0
0
0
0
0
0
1
1
0
1
1
9
A
B
0
0
0
1
1
0
1
1
0
0
0
0
1
1
1
1
C
D
E
F
1
1
1
1
1
1
1
1
8
A2
A16

Вывод: Каждые ЧЕТЫРЕ цифры двоичной системы можно записать соответствующей цифрой 16-ичной системы

Запишите!
Каждые ЧЕТЫРЕ цифры двоичной системы можно записать соответствующей цифрой 16-ичной системы
Каждые ДВЕ цифры двоичной системы можно записать соответствующей цифрой 4-ичной системы
Каждые ТРИ цифры двоичной системы можно записать соответствующей цифрой 8-ичной системы

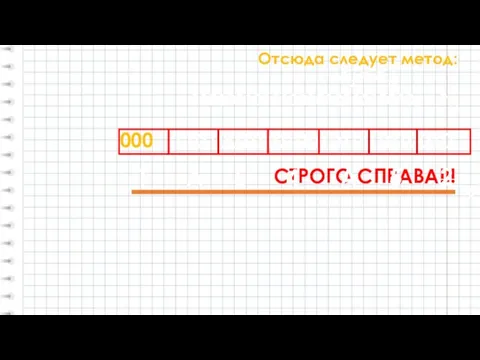
Отсюда следует метод:
11010010101001010010100102 = ?16
1101001010100101001010010
СТРОГО СПРАВА!!!
000
А2 = А16
1
A
5
4
A
5
2
16

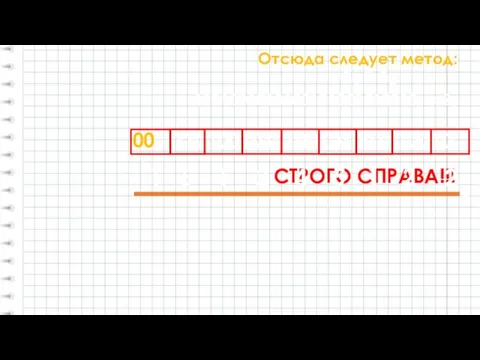
Отсюда следует метод:
11010010101001010010100102 = ?8
1101001010100101001010010
СТРОГО СПРАВА!!!
00
А2 = А8
1
5
1
8
2
2
4
5
1
2

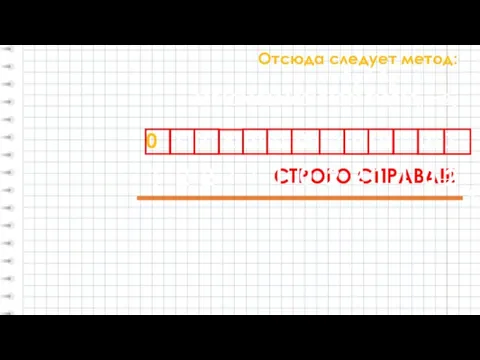
Отсюда следует метод:
11010010101001010010100102 = ?4
1101001010100101001010010
СТРОГО СПРАВА!!!
0
А2 = А4
1
2
2
1
1
1
0
4
2
2
2
1
1
0

Пройдите, пожалуйста, тестирование №1.
Для этого создайте отдельную вкладку в вашем браузере, чтобы не «потерять» трансляцию

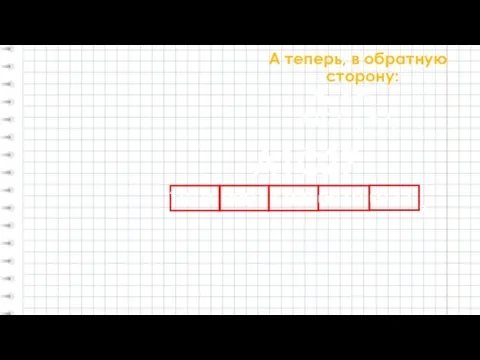
А теперь, в обратную сторону:
A1C2716 = ?2
А16 = А2
0001
1010
2
A1C27
1100
0010
0111

А теперь, в обратную сторону:
734678 = ?2
А8 = А2
011
111
2
73467
100
110
111

А теперь, в обратную сторону:
12231314 = ?2
А4 = А2
2
1223131
01
11
01
11
10
10
1
0

Пройдите, пожалуйста, тестирование №2.
Для этого создайте отдельную вкладку в вашем браузере, чтобы не «потерять» трансляцию

Обсуждение:
Можно ли такую же схему применить для переводов из А3 в А9 и А27 и обратно?