Задачи на расстояния в пространстве

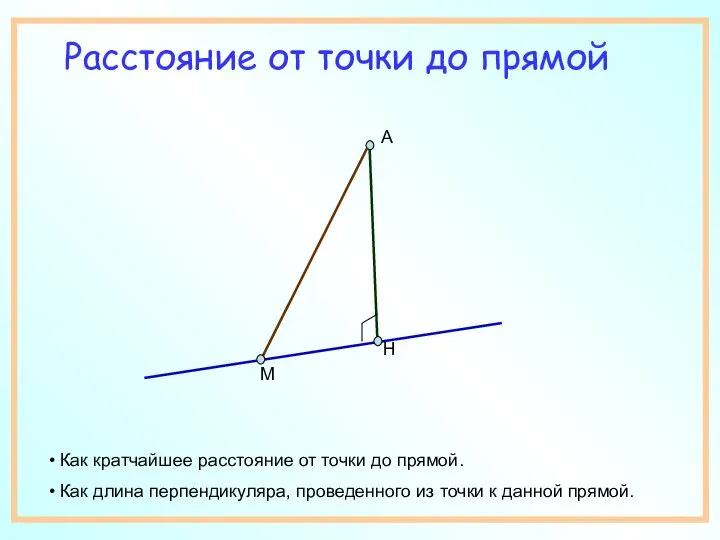
Расстояние от точки до прямой
Как кратчайшее расстояние от точки до прямой. Как длина перпендикуляра, проведенного из точки к данной прямой.

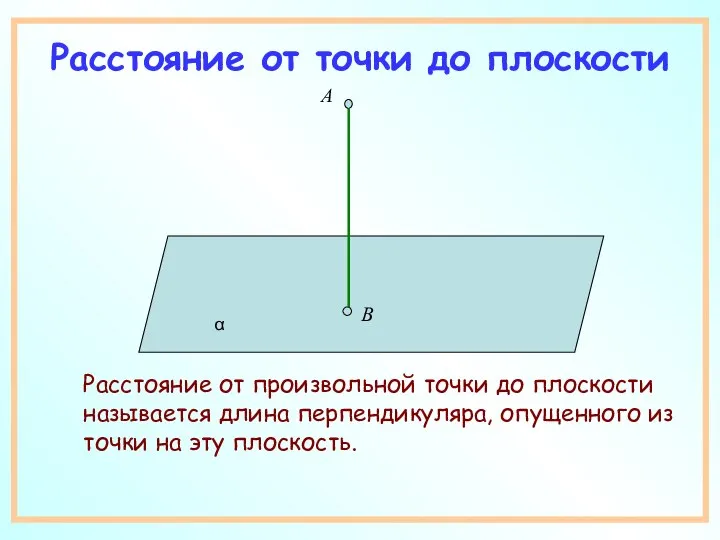
Расстояние от точки до плоскости
Расстояние от произвольной точки до плоскости называется длина перпендикуляра, опущенного из точки на эту плоскость.
В
А
α

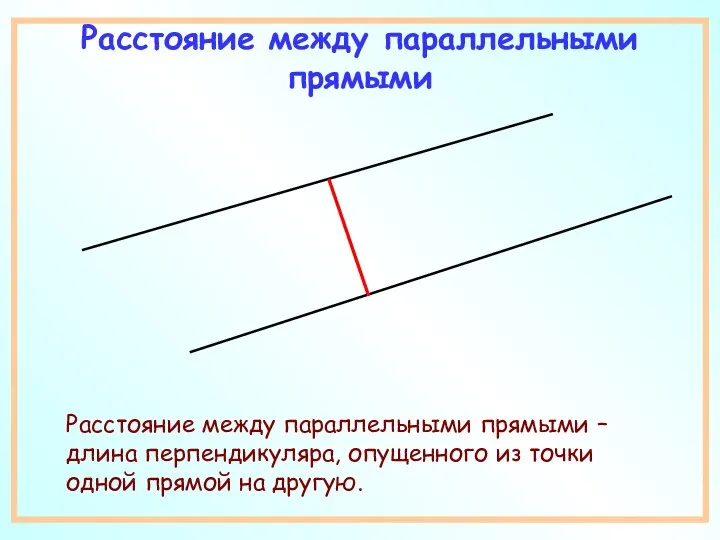
Расстояние между параллельными прямыми
Расстояние между параллельными прямыми – длина перпендикуляра, опущенного из точки одной прямой на другую.

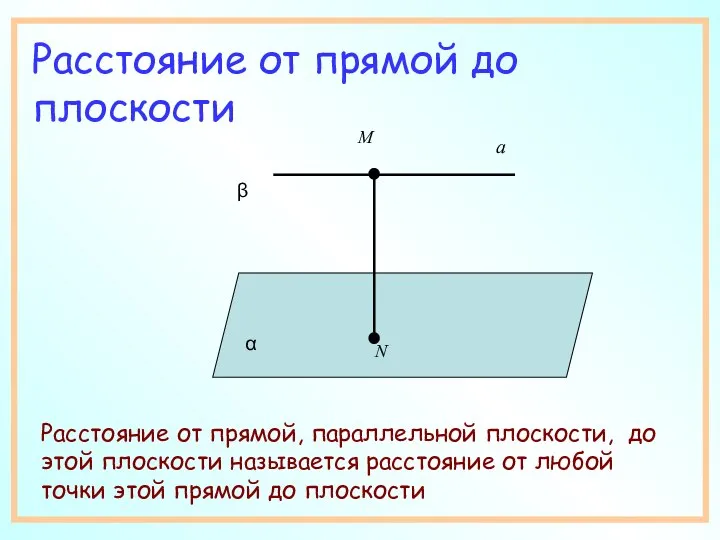
Расстояние от прямой до плоскости
Расстояние от прямой, параллельной плоскости, до этой плоскости называется расстояние от любой точки этой прямой до плоскости
а
М
β
α
N

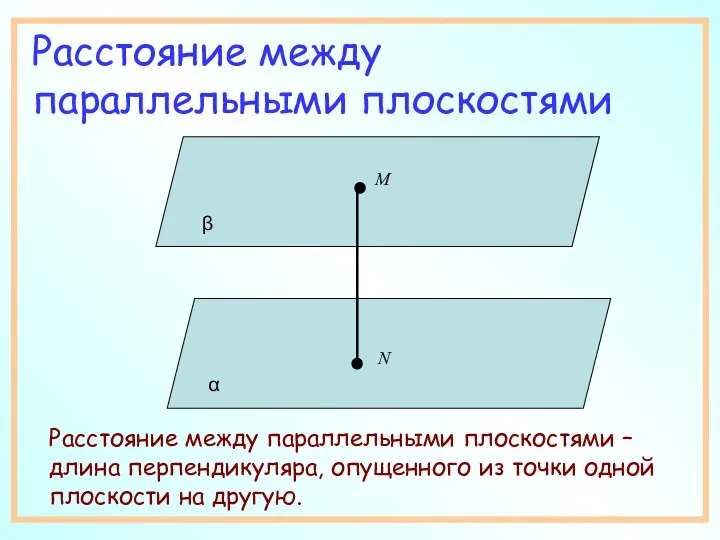
Расстояние между параллельными плоскостями
Расстояние между параллельными плоскостями – длина перпендикуляра, опущенного из точки одной плоскости на другую.
М
β
α
N

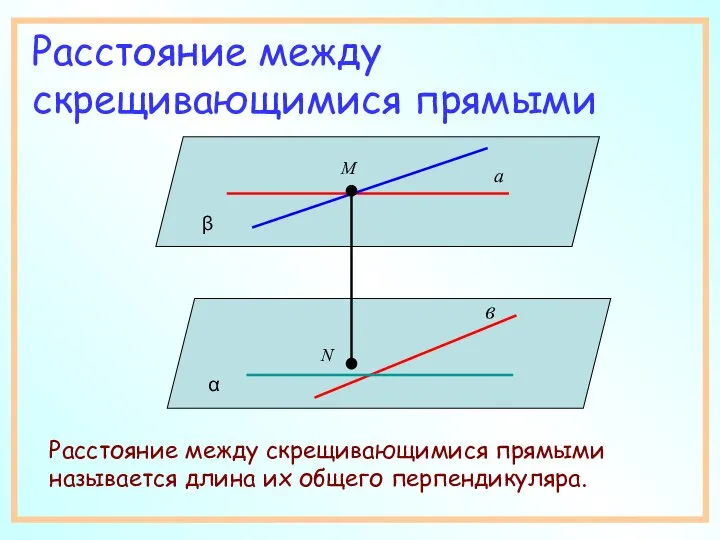
Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми называется длина их общего перпендикуляра.
а
М
β
α
N
в

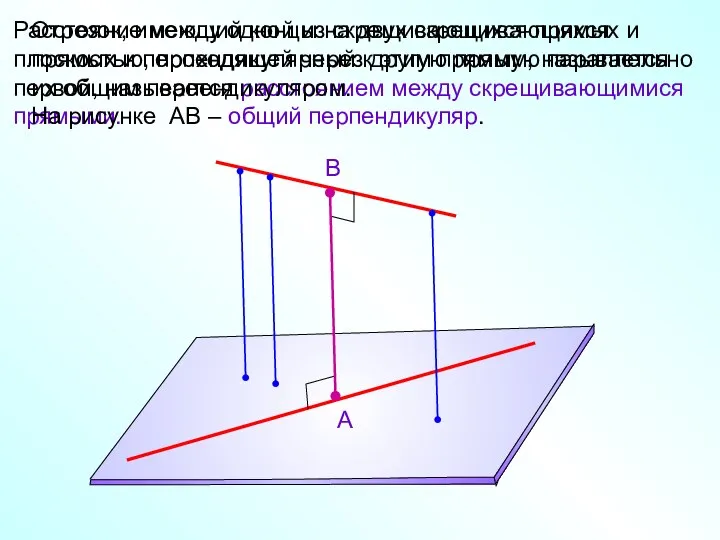
Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
Отрезок, имеющий концы на двух скрещивающихся прямых и перпендикулярный к этим прямым, называется их общим перпендикуляром.
На рисунке АВ – общий перпендикуляр.

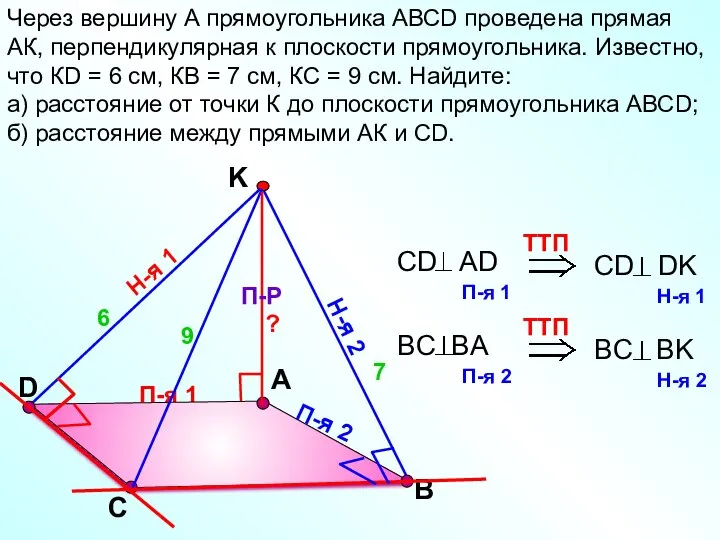
П-я 1
D
А
Через вершину А прямоугольника АВСD проведена прямая АК, перпендикулярная к плоскости прямоугольника. Известно, что КD = 6 см, КВ = 7 см, КС = 9 см. Найдите:
а) расстояние от точки К до плоскости прямоугольника АВСD; б) расстояние между прямыми АК и СD.
С
В
K
Н-я 1
Н-я 2
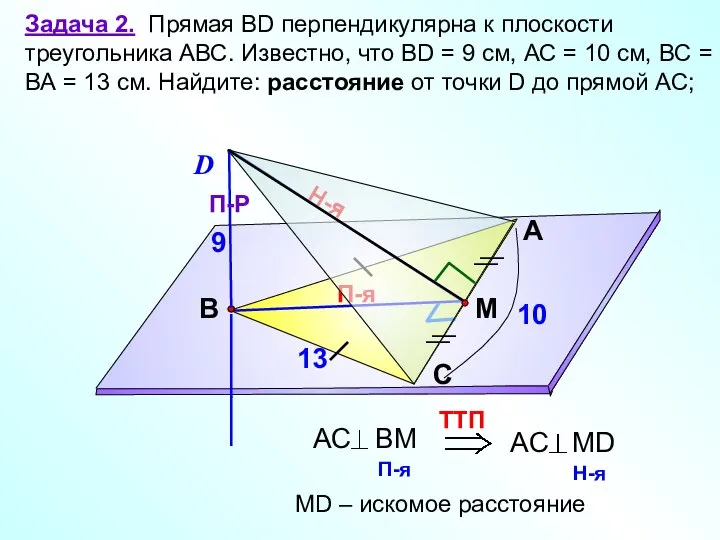
П-я 2
?

П-я
Задача 2. Прямая ВD перпендикулярна к плоскости треугольника АВС. Известно, что ВD = 9 см, АС = 10 см, ВС = ВА = 13 см. Найдите: расстояние от точки D до прямой АС;
А
С
В
П-Р
Н-я
МD – искомое расстояние

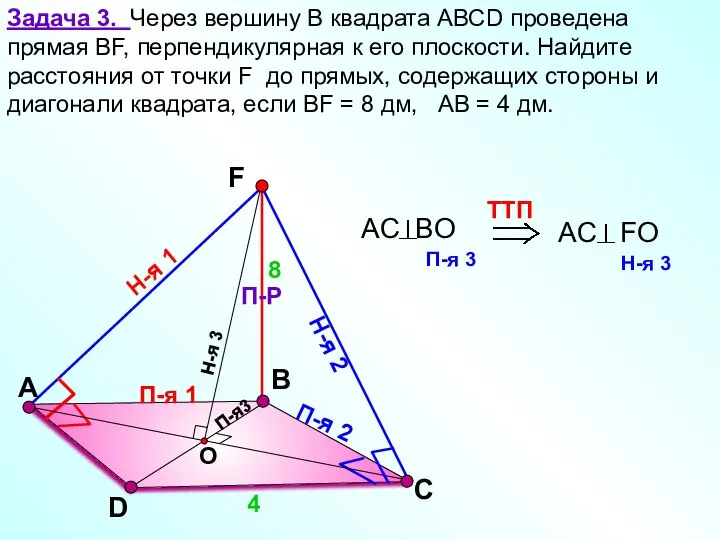
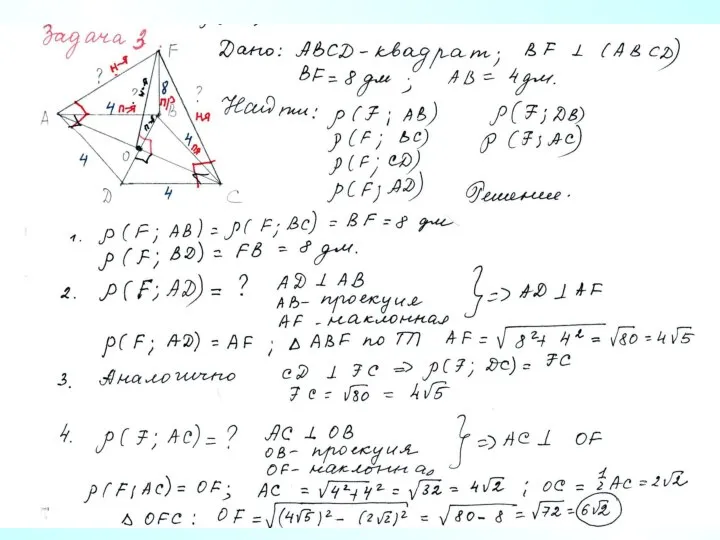
В
Задача 3. Через вершину B квадрата АВСD проведена прямая ВF, перпендикулярная к его плоскости. Найдите расстояния от точки F до прямых, содержащих стороны и диагонали квадрата, если ВF = 8 дм, АВ = 4 дм.
D
С
4
П-я 1
Н-я 1
Н-я 2
П-я 2
Н-я 3
П-я3
О
А