Содержание
- 2. План лекции Основные понятия теории систем (Система, элемент, подсистема, структура) Случайность в сложных системах Распределения случайных
- 3. В настоящее время нет единства в определении понятия "система" D1. Система есть нечто целое: S=А(1,0). Это
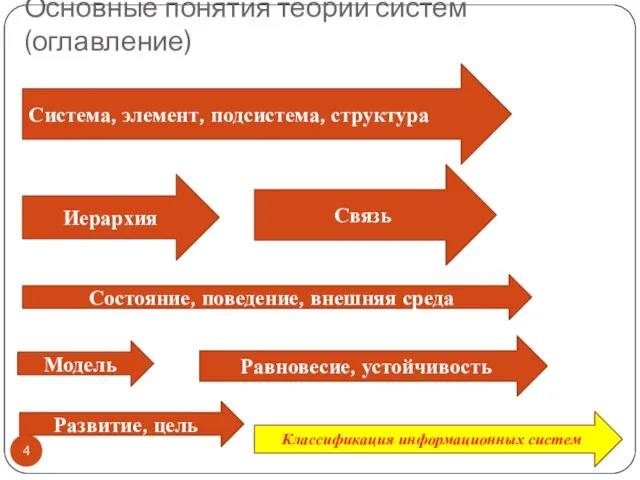
- 4. Основные понятия теории систем (оглавление) Система, элемент, подсистема, структура Иерархия Связь Состояние, поведение, внешняя среда Модель
- 5. Система, элемент, подсистема, структура В качестве "рабочего" определения понятия системы в литературе по теории систем часто
- 6. Примеры Система - городской наземный транспорт Подсистемы. Организация движения автобусов. Организация движения трамваев. Организация движения троллейбусов.
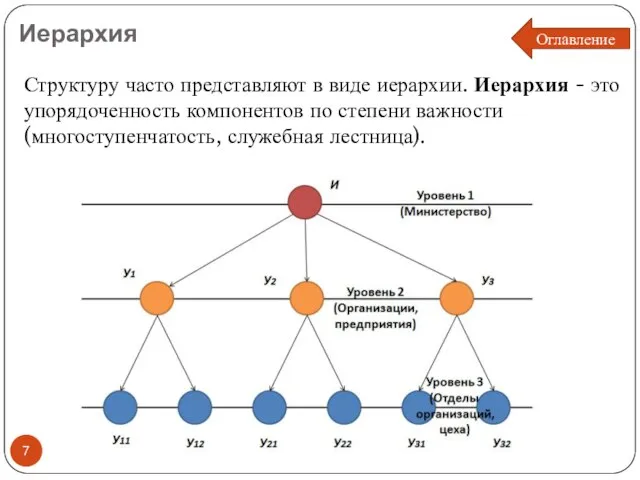
- 7. Иерархия Структуру часто представляют в виде иерархии. Иерархия - это упорядоченность компонентов по степени важности (многоступенчатость,
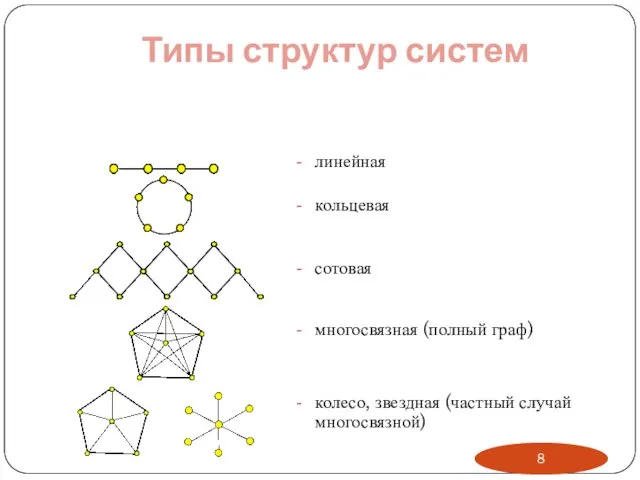
- 8. Типы структур систем линейная кольцевая сотовая многосвязная (полный граф) колесо, звездная (частный случай многосвязной)
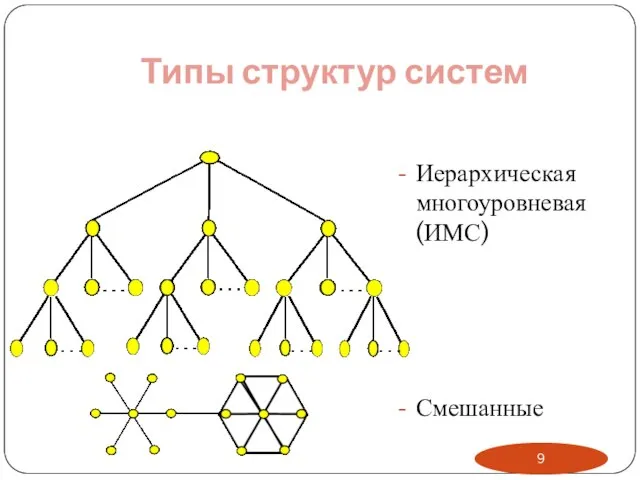
- 9. Типы структур систем Иерархическая многоуровневая (ИМС) Смешанные
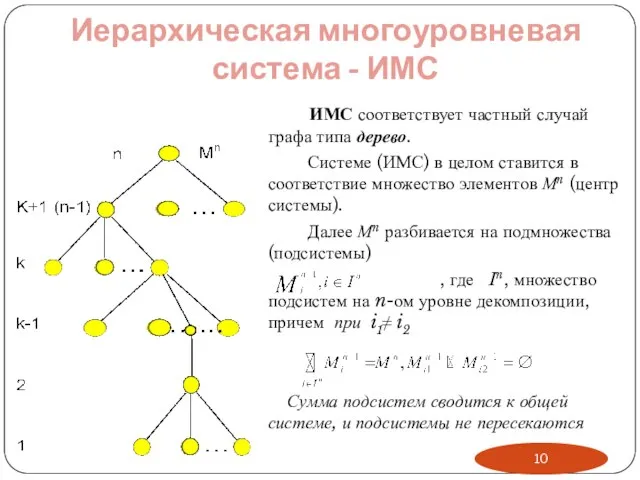
- 10. Иерархическая многоуровневая система - ИМС ИМС соответствует частный случай графа типа дерево. Системе (ИМС) в целом
- 11. Пирамидальность – на самом верхнем (n- ом) уровне находится только один элемент. Ветвистость – элемент k-го
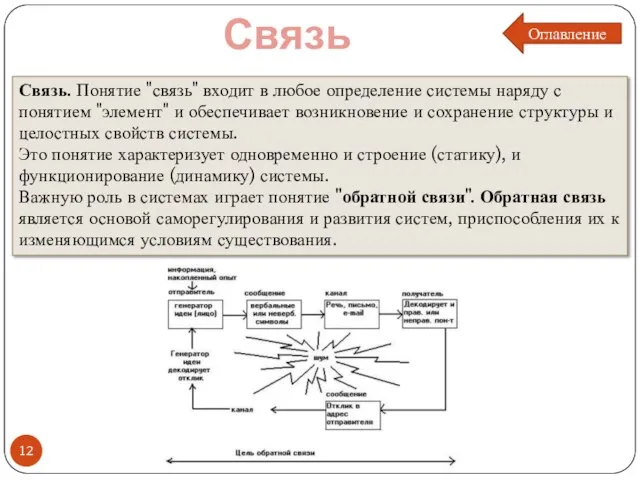
- 12. Связь Связь. Понятие "связь" входит в любое определение системы наряду с понятием "элемент" и обеспечивает возникновение
- 13. Состояние, поведение, внешняя среда Состояние. Понятием "состояние" обычно характеризуют мгновенную фотографию, "срез" системы, остановку в ее
- 14. Модель Модель. Под моделью системы понимается описание системы, отображающее определенную группу ее свойств. Оглавление
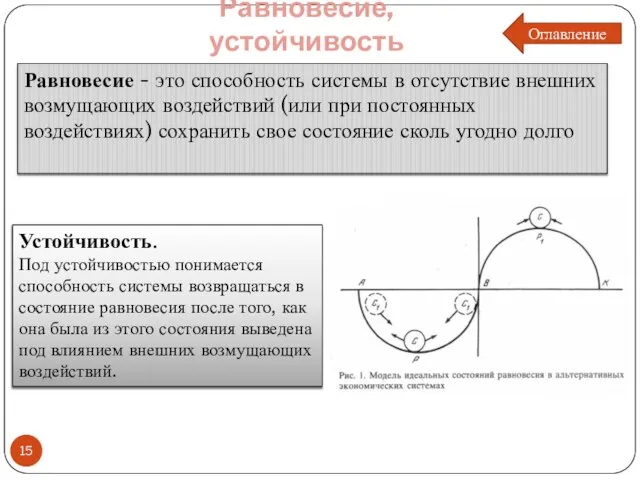
- 15. Равновесие, устойчивость Равновесие - это способность системы в отсутствие внешних возмущающих воздействий (или при постоянных воздействиях)
- 16. Развитие, цель Развитие. Исследованию процесса развития, соотношения процессов развития и устойчивости, изучению механизмов, лежащих в их
- 17. Классификация информационных систем по виду отображаемого объекта—технические, биологические, экономические и др.; по виду научного направления —
- 18. Случайные события и величины Случайность в системах
- 19. Случайные события Случайным событием это всякое явление, которое в результате испытания может произойти или не произойти.
- 20. Случайные события Достоверное событие обязательно произойдет приданном комплексе условий. Например, если в сосуде находится вода, давление
- 21. Итак, имеется схема для различных событий, наступающих при неизменном комплексе условий: достоверное – случайное – невозможное.
- 22. Факторы случайности при использовании ИМ
- 23. Случайная величина Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение,
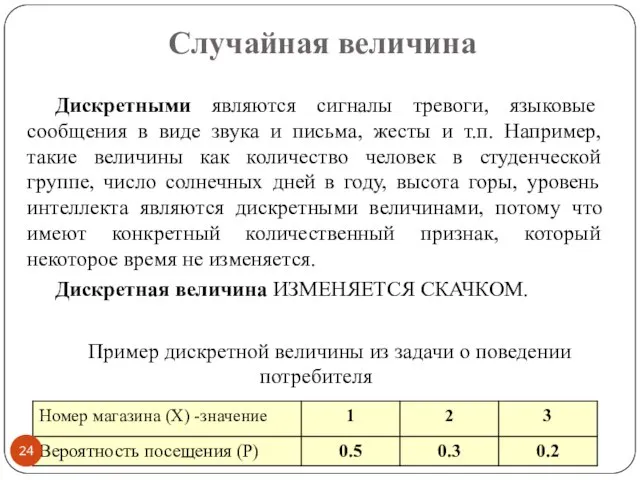
- 24. Случайная величина Дискретными являются сигналы тревоги, языковые сообщения в виде звука и письма, жесты и т.п.
- 25. Распределения случайных величин Непрерывные случайные величины Дискретные случайные величины Методы подбора распределений для эксперимента
- 26. Непрерывные распределения Равномерное Экспоненциальное Гамма-распределение Вейбулла Нормальное Логнормальное Бета-распределение Распределение Пирсона Логистическое распределение Распределение Джонсона Треугольное
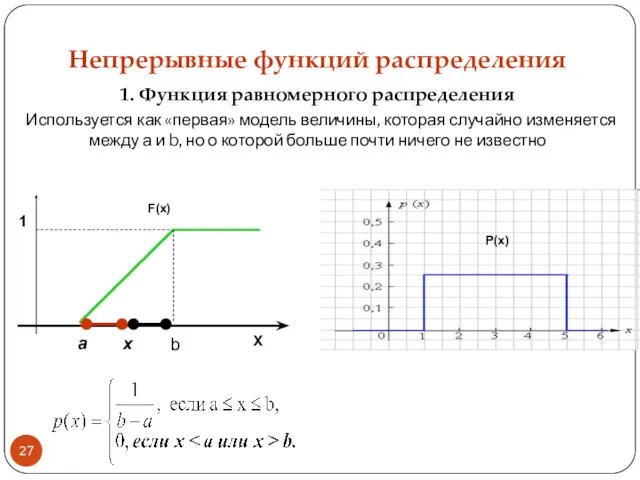
- 27. Непрерывные функций распределения 1. Функция равномерного распределения Используется как «первая» модель величины, которая случайно изменяется между
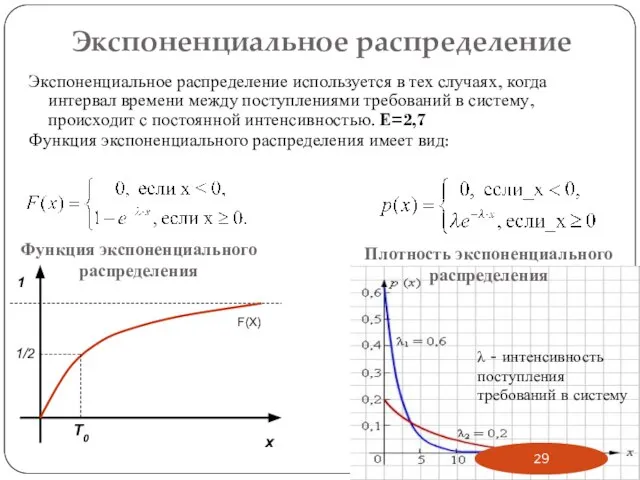
- 28. Экспоненциальное распределение Это распределение применяется для представления промежутка времени между случайными событиями, например, времени между прибытиями
- 29. Экспоненциальное распределение Экспоненциальное распределение используется в тех случаях, когда интервал времени между поступлениями требований в систему,
- 30. Экспоненциальное распределение Пример 1. Пусть есть магазин, в который время от времени заходят покупатели. При определённых
- 31. Экспоненциальное распределение Моделирует время между двумя последовательными появлениями одного и того же события. Например, время между
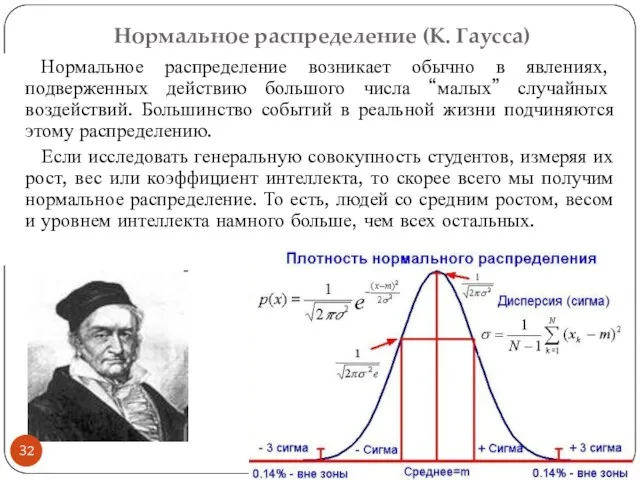
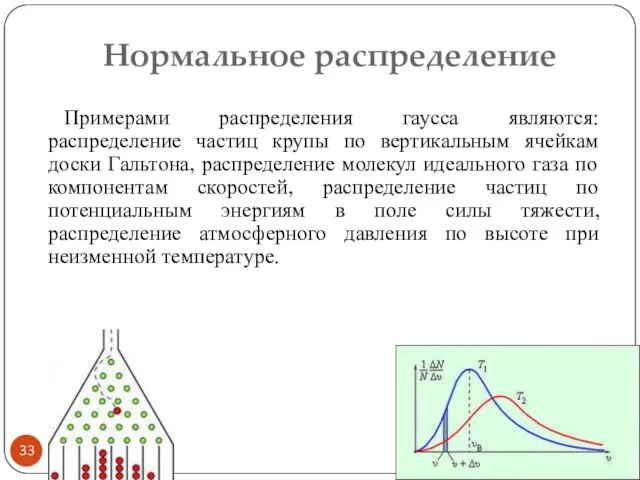
- 32. Нормальное распределение (К. Гаусса) Нормальное распределение возникает обычно в явлениях, подверженных действию большого числа “малых” случайных
- 33. Нормальное распределение Примерами распределения гаусса являются: распределение частиц крупы по вертикальным ячейкам доски Гальтона, распределение молекул
- 35. Распределение Вейбулла Семейство распределений Вейбулла является двухпараметрическим и описывает Положительные случайные величины. Считается, что распределению Вейбулла
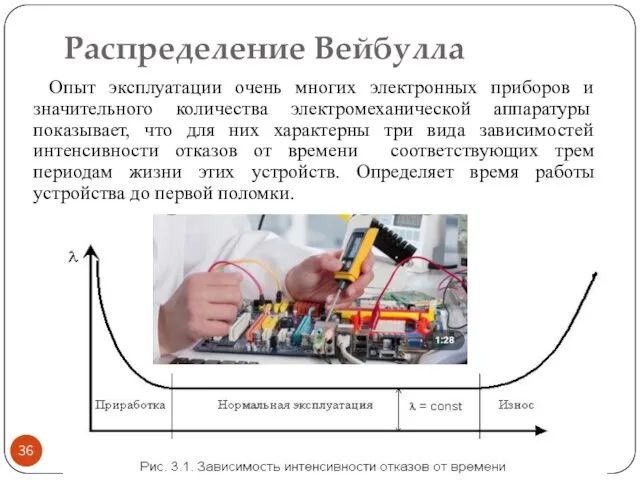
- 36. Распределение Вейбулла Опыт эксплуатации очень многих электронных приборов и значительного количества электромеханической аппаратуры показывает, что для
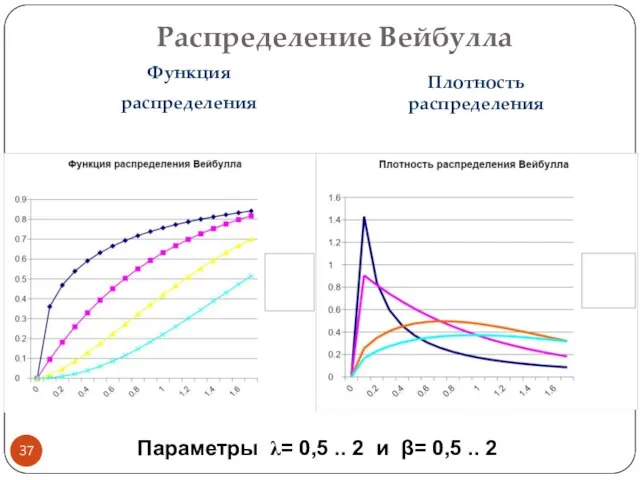
- 37. Распределение Вейбулла Функция распределения Плотность распределения Параметры λ= 0,5 .. 2 и β= 0,5 .. 2
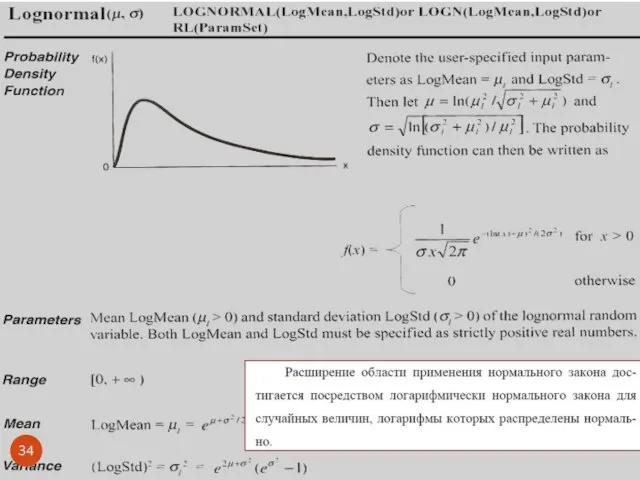
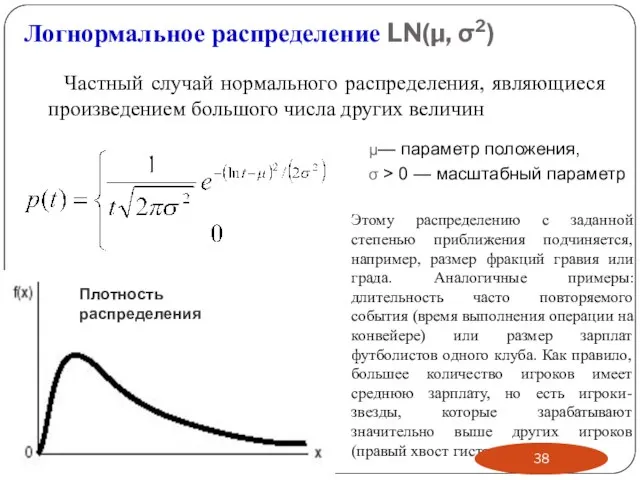
- 38. Логнормальное распределение LN(μ, σ2) Частный случай нормального распределения, являющиеся произведением большого числа других величин Плотность распределения
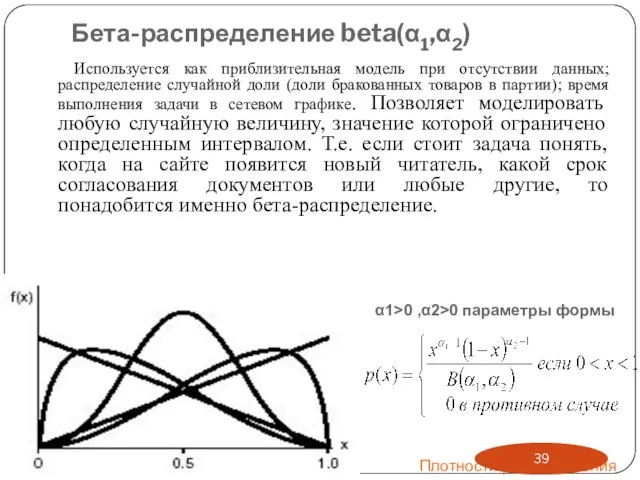
- 39. Бета-распределение beta(α1,α2) Используется как приблизительная модель при отсутствии данных; распределение случайной доли (доли бракованных товаров в
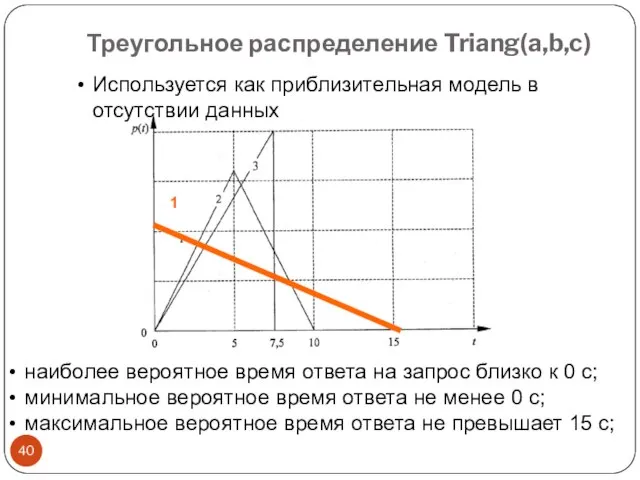
- 40. Треугольное распределение Triang(a,b,c) наиболее вероятное время ответа на запрос близко к 0 с; минимальное вероятное время
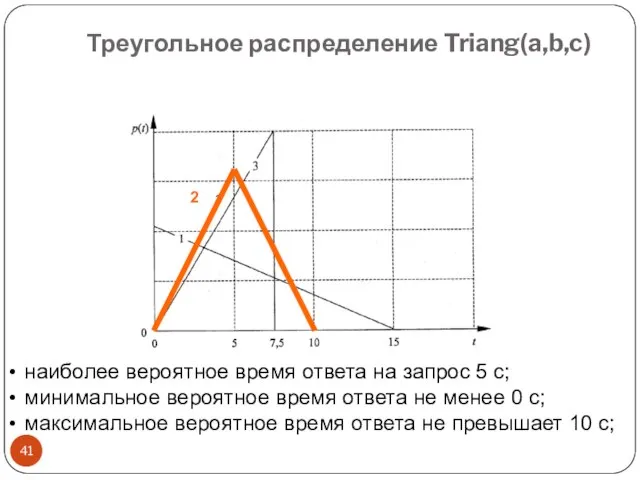
- 41. Треугольное распределение Triang(a,b,c) наиболее вероятное время ответа на запрос 5 с; минимальное вероятное время ответа не
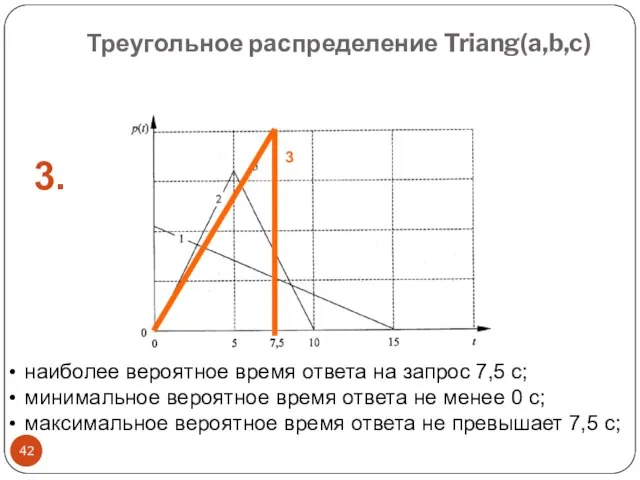
- 42. Треугольное распределение Triang(a,b,c) наиболее вероятное время ответа на запрос 7,5 с; минимальное вероятное время ответа не
- 43. Распределения дискретных случайных величин Подготовка данных для ИМ Дискретные законы распределения
- 44. Дискретные и непрерывные величины все процессы, происходящие в природе, делятся на непрерывные и дискретные. примерами непрерывных
- 45. Случайная величина Дискретными являются сигналы тревоги, языковые сообщения в виде звука и письма, жесты и т.П.
- 46. Дискретные распределения Распределение Бернулли Биномиальное распределение Распределение Пуассона Геометрическое распределение Равномерное распределение Логарифмическое распределение
- 47. Дискретные распределения Дискретные величины могут принимать только конечное или счетное множество определенных значений. Например, число очков
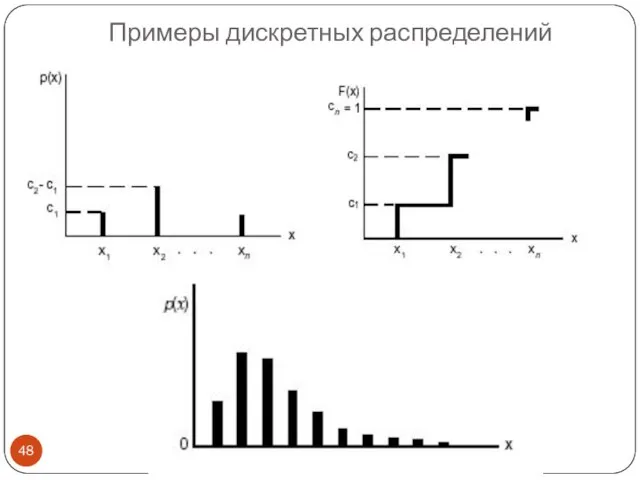
- 48. Примеры дискретных распределений
- 49. Дискретные распределения Дискретное распределение характеризуется тем, что оно сосредоточено в конечном или счетном числе точек. Распределение
- 50. Распределение Якоба Бернулли Биномиальное распределение является распределением числа успехов μ в n испытаниях бернулли с вероятностью
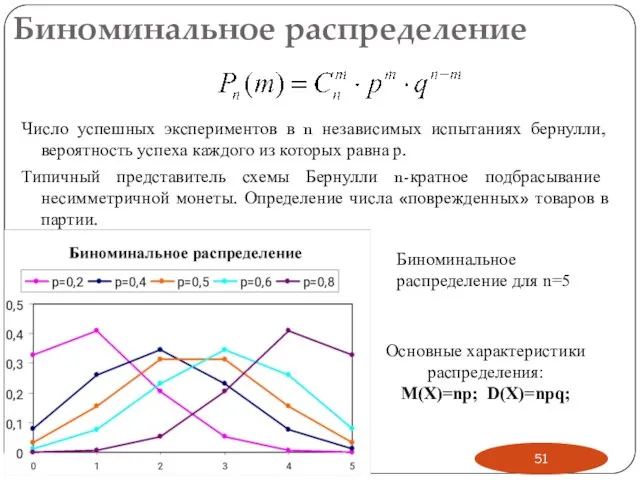
- 51. Биноминальное распределение Число успешных экспериментов в n независимых испытаниях бернулли, вероятность успеха каждого из которых равна
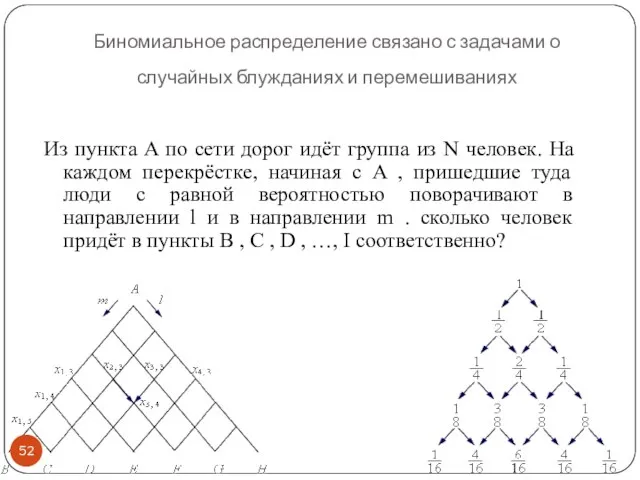
- 52. Биномиальное распределение связано с задачами о случайных блужданиях и перемешиваниях Из пункта A по сети дорог
- 53. Закон Пуассона По закону Пуассона распределены, например, число вызовов, поступивших на телефонную станцию в короткий промежуток
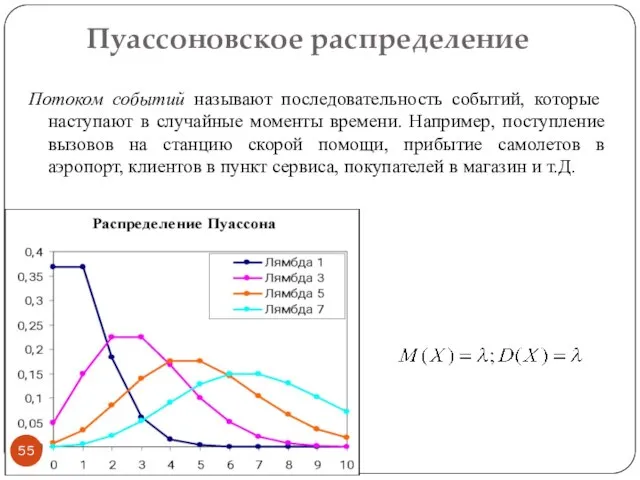
- 54. Пуассоновское распределение Дискретная случайная величина ξ распределена по закону Пуассона, если она принимает целые неотрицательные значения
- 55. Пуассоновское распределение Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Например, поступление вызовов
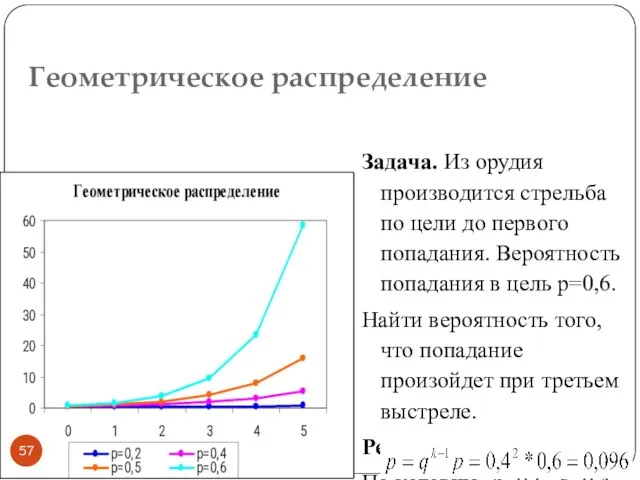
- 56. Геометрическое распределение Если проводятся независимые испытания бернулли и подсчитывается количество испытаний до наступления успеха, то это
- 57. Геометрическое распределение Задача. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель
- 58. Гипергеометрическое распределение Дискретная случайная величина X имеет гипергеометрическое распределение, если она принимает значения 0, 1, 2,
- 59. Равномерное распределение Случайная величина имеет дискретное равномерное распределение, если она принимает конечное число значений с равными
- 60. Дискретное равномерное распределение Дискретное равномерное распределение – случайное событие, имеющее несколько возможных результатов с одинаковой вероятностью
- 61. Логарифимическое распределение Логарифмическое распределение используется в различных приложениях, включая математическую генетику и физику. Например, строение моллюсков,
- 62. Метод Монте-Карло для моделирования систем
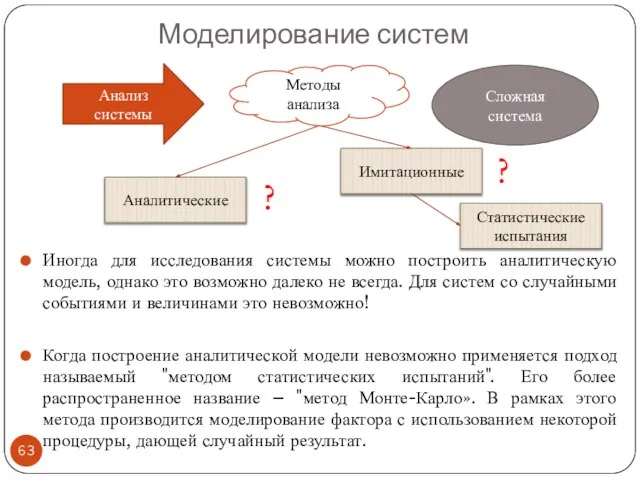
- 63. Моделирование систем Иногда для исследования системы можно построить аналитическую модель, однако это возможно далеко не всегда.
- 64. Метод Монте-Карло При моделировании случайных явлений методом Монте-Карло мы пользуемся самой случайностью как аппаратом исследования, заставляем
- 65. Метод Монте-Карло Метод Монте-Карло - это численный метод решения имитационных задач при помощи моделирования (ГЕНЕРАЦИИ) случайных
- 66. Метод Монте-Карло Идея метода чрезвычайно проста и состоит в следующем. Производится «розыгрыш» случайного явления с помощью
- 67. Генерация случайных чисел на ЭВМ При компьютерном моделировании возникает задача генерации случайных числовых последовательностей с заданными
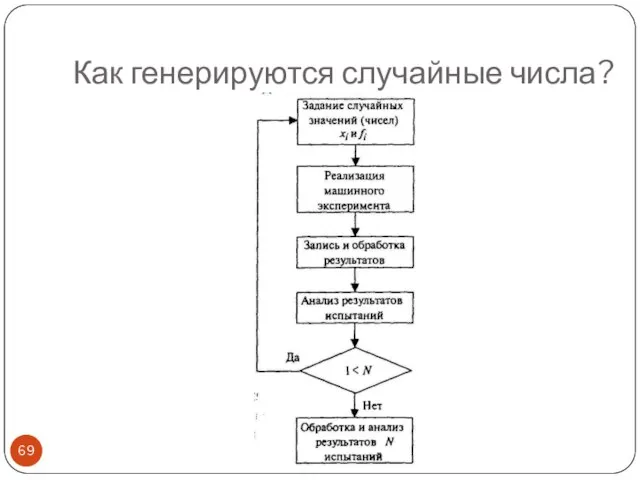
- 68. Как генерируются случайные числа? Вначале получают последовательность равномерно распределенных на интервале [0, 1] псевдослучайных чисел. Из
- 69. Как генерируются случайные числа?
- 70. Методы генерации равномерного распределения Известно большое количество методов имитации равномерного распределения: методы середины квадратов, вычетов, суммирования,
- 71. Метод середины квадрата Метод середины квадрата хорошо "перемешивает" предыдущее число. Однако он имеет недостатки: если какой-нибудь
- 72. Области использования метода Монте-Карло Создание последовательности случайных величин для задач моделирования систем и процессов из области
- 73. Точность метода Монте-Карло Допустим в областях, где допускается уровень ошибки 5-10%
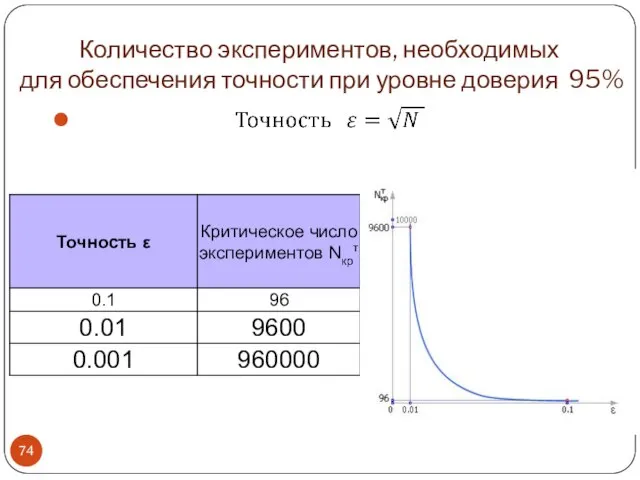
- 74. Количество экспериментов, необходимых для обеспечения точности при уровне доверия 95% Постро
- 75. Методы определения распределений Использование системных входных данных за прошлое время Может воспроизводиться только то, что уже
- 77. Скачать презентацию













































 Параллельные плоскости
Параллельные плоскости Приёмы умножения на 2
Приёмы умножения на 2 Математика 4 класс
Математика 4 класс Презентация на тему Прибавление и вычитание числа 3
Презентация на тему Прибавление и вычитание числа 3  Математика в профессии Застройщик
Математика в профессии Застройщик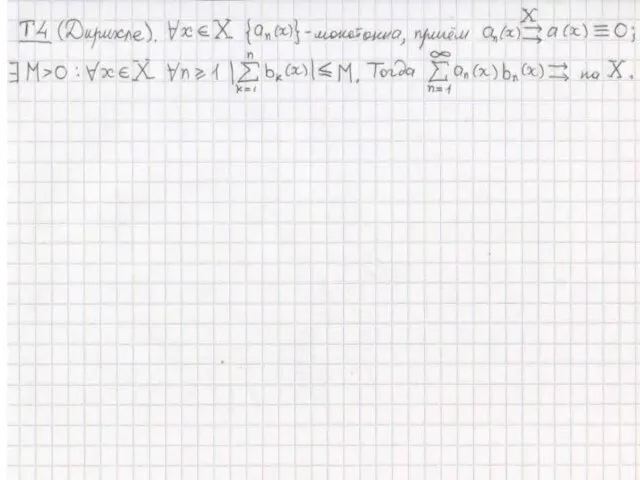 Свойства равномерно-сходящихся плоскостей и рядов
Свойства равномерно-сходящихся плоскостей и рядов Презентация на тему Пропорции
Презентация на тему Пропорции  Перетворення графіків
Перетворення графіків Многогранники. Розв'язування задач
Многогранники. Розв'язування задач Тренажёр. Единицы измерения
Тренажёр. Единицы измерения Обыкновенные дроби
Обыкновенные дроби Устная работа. Вычисления
Устная работа. Вычисления Вычисление реакций и перемещений в статически неопределимых системах
Вычисление реакций и перемещений в статически неопределимых системах Перпендикулярные прямые
Перпендикулярные прямые Функциональная грамотность (математика) - задачи
Функциональная грамотность (математика) - задачи Решение тригонометрических уравнений
Решение тригонометрических уравнений Алгоритм письмового додавання, якщо сума розрядних одиниць дорівнює 10
Алгоритм письмового додавання, якщо сума розрядних одиниць дорівнює 10 Сложение отрицательных чисел
Сложение отрицательных чисел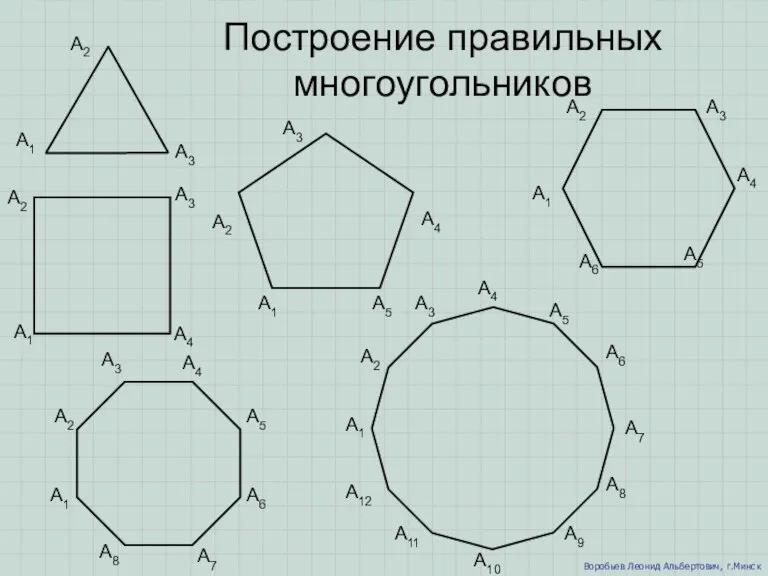 Построение правильных многоугольников
Построение правильных многоугольников Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота
Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота Совокупность математических методов для изучения свойств кубика Рубика
Совокупность математических методов для изучения свойств кубика Рубика Золотое сечение. Витрувий
Золотое сечение. Витрувий Презентация на тему Кто хочет стать математиком
Презентация на тему Кто хочет стать математиком  Решение логарифмических уравнений к занятию
Решение логарифмических уравнений к занятию Понятие и виды средних величин
Понятие и виды средних величин Презентация на тему Вклад Пифагора в развитие музыки 7 класс
Презентация на тему Вклад Пифагора в развитие музыки 7 класс  Квадратные неравенства с параметрами
Квадратные неравенства с параметрами Логарифм и его свойства
Логарифм и его свойства