Лекция№7

Нелинейная интерполяция

Нелинейная интерполяция
Стараются подобрать такое преобразование переменных η=η(у) ; ξ=ξ(х), чтобы в новых переменных график функции η(ξ) мало отличался от прямой линии на протяжении нескольких шагов таблицы.
Метод выравнивания
Составляют таблицу ηi=η(ξi), интерполируют по ней и обратным преобразованием находят у=у(η).

Нелинейная интерполяция
Сделаем замену ξ=х; η=lg y и составим новую таблицу:
Метод выравнивания
Интерполяция с помощью интерполяционного полинома Ньютона N3(ξ=0.5)≈0.5203 ⇒
⇒ у=100.5203 ≈ 3.314

Обратное интерполирование
Обратное интерполирование – процесс нахождения x для произвольного y, если задана таблица yk = f (xk).
прямое интерполирование
обратное интерполирование
Метод обратного интерполирования позволяет найти корень уравнения f(x)=0 для заданной таблично функции f.

Обратное интерполирование
По таблице {yk; xk} cтроим интерполяционный полином
Находим значение полинома для y=0.
Это значение и будет корнем уравнения f(x)=0, т.е. x* = Ln(0).
Для достаточно гладких функций этот способ дает хорошие результаты.

Интерполирование сплайнами
Интерполяция на больших отрезках приводит к плохому приближению:
Если взять мало узловых точек, то точность будет очень мала;
Если взять много точек, то возрастает вычислительная погрешность.
Поэтому используют кусочную интерполяцию более низкого порядка:
Весь отрезок разбивается на части;
На каждой части отрезка интерполяцию проводят по небольшому числу узловых точек;
Все интерполяционные полиномы объединяют в одну интерполяционную формулу.

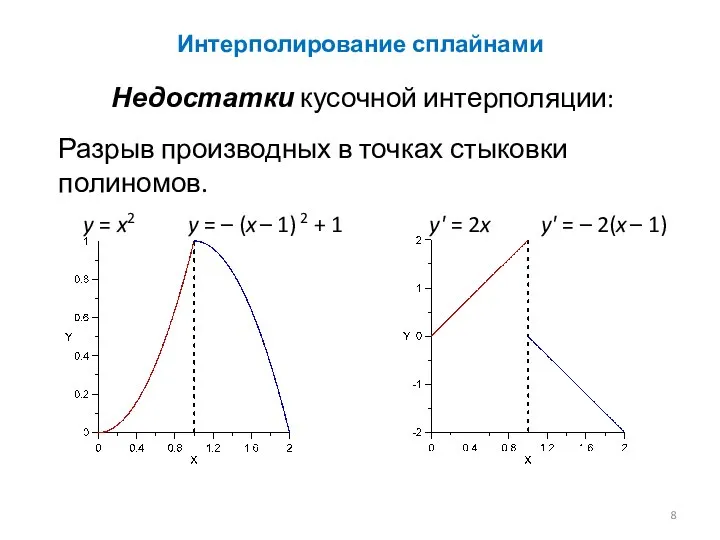
Интерполирование сплайнами
Недостатки кусочной интерполяции:
Разрыв производных в точках стыковки полиномов.
y = x2
y = – (x – 1) 2 + 1
y' = 2x
y' = – 2(x – 1)

Интерполирование сплайнами
Для построения интерполяционной функции с гладкими производными используют сплайн-интерполяцию.
spline [англ]- гибкая линейка.
Сплайн-функцией, или сплайном, называют кусочно-полиномиальную функцию, определенную на отрезке [a, b] и имеющую на этом отрезке некоторое число непрерывных производных.
Дефектом сплайна называется разница между степенью сплайна и порядком наивысшей непрерывной на [a, b] производной.

Интерполирование сплайнами
Рассмотрим кубический сплайн.
Пусть на [a, b] задана непрерывная функция f(x). Введем сетку а=х0
Механическая интерпретация сплайн-интерполяции:
Будучи деформированной и проходя через фиксированные точки, линейка приобретает форму, при которой запасенная в ней упругая энергия минимальна.

Интерполирование сплайнами
Интерполяционным кубическим сплайном называется функция S(x), удовлетворяющая следующим условиям:
а) На каждом отрезке [xk–1, xk], k=1,2,…,n, функция S(x) является полиномом 3-ей степени;
б) Функция S(x), а также ее первая и вторая производные непрерывны на [a,b];
в) S(xk)=f(xk), k=0,1,...,n (условие интерполяции).

Интерполирование сплайнами
Будем искать кубический сплайн в виде:
Следовательно, требуется определить 4n коэффициента ak, bk, ck, dk .
Для определения этих коэффициентов используем свойства кубического сплайна:
1) Условие интерполяции
где
2n
(1)
(2)

Интерполирование сплайнами
2) Условия непрерывности производных в узловых точках
Очевидно
Тогда
2n–2
(3)
(4)

Интерполирование сплайнами
3) Недостающие два уравнения получают из условий на границах отрезка.
Способы задания граничных условий:
1. Заданы первые производные
2. Заданы вторые производные
3. Равенство первых и вторых производных справа и слева (периодичность)

Интерполирование сплайнами
4. Непрерывность третьих производных в точках х1 и хn–1, то есть сплайн выражается одним кубическим многочленом на отрезках [x0, x2] и [xn–2, xn]:
Комбинация условий 1 – 4: на одной границе задано условие одного типа, на другой – другого типа.
Рассмотрим случай, когда первые производные имеют постоянное значение
(или, вторые производные равны нулю).

Интерполирование сплайнами
Тогда
или
2
Решим систему уравнений следующим образом
(5)
(6)
Исключим ak из уравнений (1) и (2)
Выразим bk

Интерполирование сплайнами
Перепишем, увеличив индекс на 1:
Выразим dk из уравнения (4) через сk:
И подставим в предыдущее уравнение:
(7)
(8)
(9)

Интерполирование сплайнами
Из (5)
В итоге получили систему уравнений для нахождения коэффициентов ck , k=1... n – 2.
Из (4) и (6)
bk , bk+1 , dk из (7) - (9) подставим в (3).

Интерполирование сплайнами
Система имеет вид:
Эта система имеет трехдиагональную матрицу и решается методом прогонки.

Интерполирование сплайнами
Коэффициенты dk находим из (7); k = 1,…,n
После решения системы будут известны ck.
Коэффициенты bk находим из (8); k = 1,…,n
Коэффициенты аk находим из (1); k = 1,…,n
Сплайн
построен.

Аппроксимация по методу наименьших квадратов
Точное воспроизведение значений функции в узловых точках далеко не всегда является необходимым, а иногда даже нецелесообразно:
1) Работать с глобальными интерполяционным полиномом неудобно, кроме того при его вычислении будет накапливаться вычислительная погрешность.

Аппроксимация по методу наименьших квадратов
2) Табличные данные чаще всего являются результатами каких-то измерений и содержат ошибки – как случайные, так и систематические.
Построение аппроксимирующего многочлена с условием обязательного прохождения его графика через эти экспериментальные точки означало бы тщательное повторение допущенных при измерениях ошибок!

Аппроксимация по методу наименьших квадратов
Выход из этого положения:
Найти такой многочлен (степени более низкой, чем n), который хотя и не дает точных значений функции в узлах, но достаточно близко к ним подходит.
Словам «близко подходит» можно придавать различный смысл , и в зависимости от этого получать различные аппроксимационные многочлены.
Возможны различные критерии аппроксимации.

Аппроксимация по методу наименьших квадратов

Аппроксимация по методу наименьших квадратов
На практике часто допускают, что отдельные отклонения могут быть велики, но требуют, чтобы отклонения F(x) от f(x) были малы в среднем.
За меру отклонения принимают величину:
Эта величина называется
квадратичным отклонением.

Аппроксимация по методу наименьших квадратов