- Главная
- Математика
- Начертательная геометрия. Проецирование прямой линии

Содержание
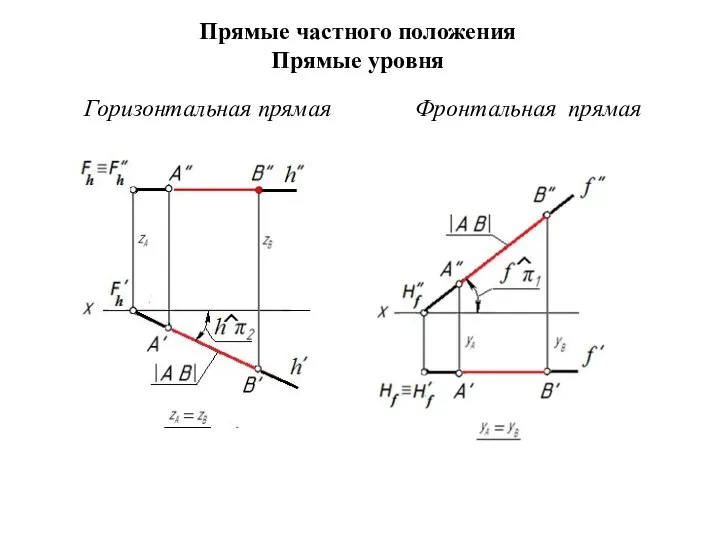
- 2. Прямые частного положения Прямые уровня Горизонтальная прямая Фронтальная прямая
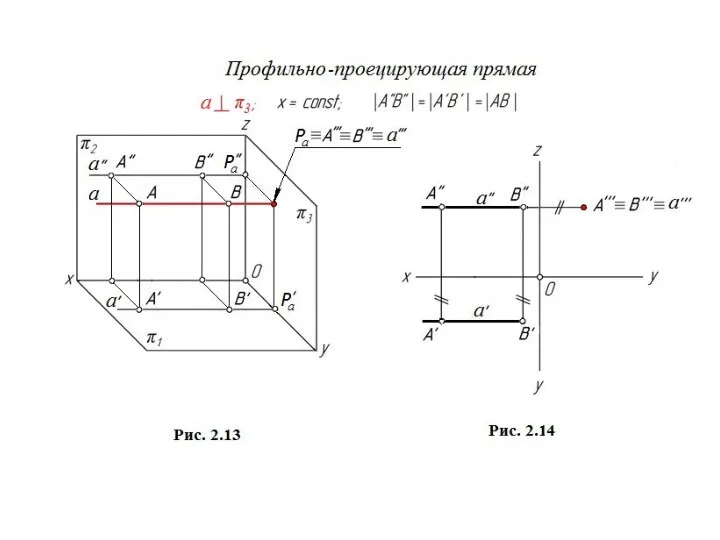
- 3. Профильная прямая
- 4. В учебнике по геометрии (автор Атанасян Л.С. и др. Геометрия для 10-11 кл. М.: Просвещение. 2009.
- 5. Проецирующие прямые
- 7. Правило Определение длины отрезка прямой общего положения и углов наклона прямой к плоскостям проекций Следует построить
- 9. Скачать презентацию
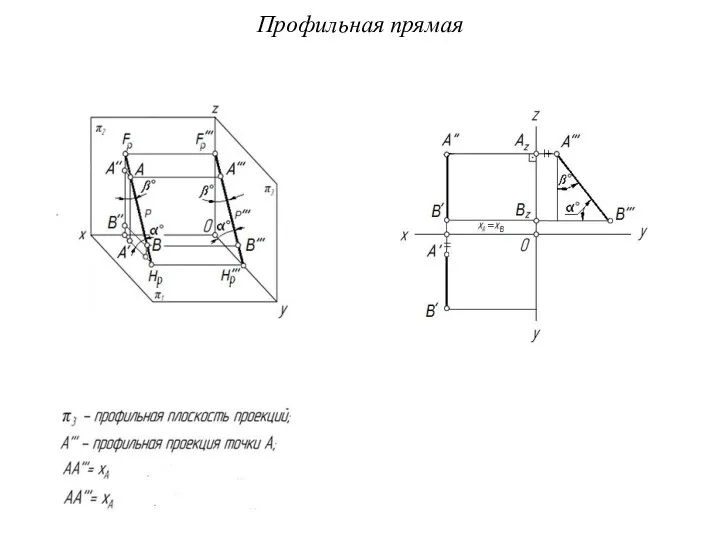
Слайд 3Профильная прямая
Профильная прямая
Слайд 4В учебнике по геометрии (автор Атанасян Л.С. и др. Геометрия для 10-11
В учебнике по геометрии (автор Атанасян Л.С. и др. Геометрия для 10-11

кл. М.: Просвещение. 2009. 207 с.) приведена с доказательством задача №132): «Доказать, что если прямая параллельна плоскости, то все точки прямой равноудалены от плоскости
Дано:
Прямая a || α
Доказать: все точки прямой a равноудалены от плоскости α.
Доказательство
Выберем на прямой a две произвольные точки А и В.
Докажем, что расстояния от точки А и от точки В до плоскости α равны: ААα = ВВα.
Если прямая a параллельна плоскости α, то в плоскости α содержится множество прямых, параллельных данной прямой a, например, прямая a1.
Определим расстояния от точек А и В до плоскости α - ААα и ВВα:
ААα α и ВВα α. Так как перпендикуляра к одной плоскости параллельны, то
ААα || В Вα.
Проведем АА1 || ВВ1, соединим точки Аα и А1 Вα и В1 и рассмотрим два равных треугольника - ААαА1 и ВВαВ1: АА1 = ВВ1 как отрезки параллельных прямых, заключенных между двумя другими параллельными прямыми; АαА1 = ВαВ1 как проекции равных наклонных.
Из равенства треугольников следует, что ААα = ВВα – что и требовалось доказать.
Слайд 5
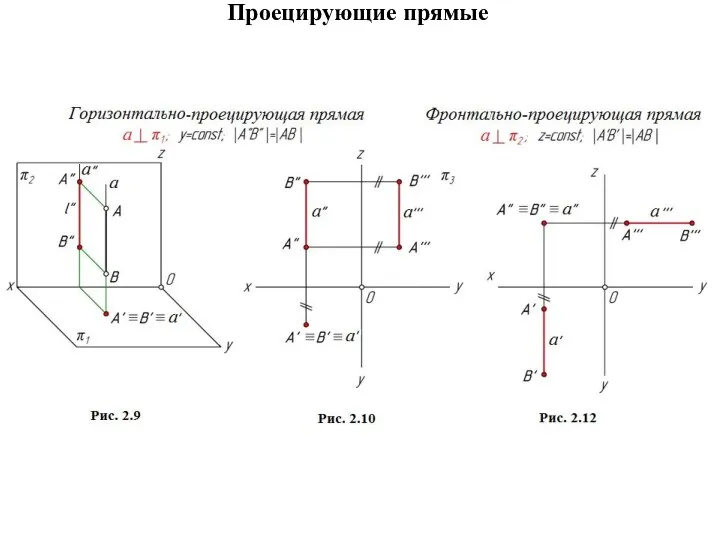
Проецирующие прямые
Проецирующие прямые
Слайд 7Правило
Определение длины отрезка прямой общего положения и углов наклона прямой к
Правило
Определение длины отрезка прямой общего положения и углов наклона прямой к

плоскостям проекций
Следует построить прямоугольный треугольник, одним катетом которого является горизонтальная (фронтальная) проекция отрезка, другим катетом - абсолютная величина алгебраической разности аппликат (ординат) концов отрезка.
Гипотенуза будет равна длине отрезка, а угол между гипотенузой и катетом, равным горизонтальной (фронтальной) проекции отрезка, равен углу наклона отрезка к горизонтальной (фронтальной) плоскости проекций.
Следует построить прямоугольный треугольник, одним катетом которого является горизонтальная (фронтальная) проекция отрезка, другим катетом - абсолютная величина алгебраической разности аппликат (ординат) концов отрезка.
Гипотенуза будет равна длине отрезка, а угол между гипотенузой и катетом, равным горизонтальной (фронтальной) проекции отрезка, равен углу наклона отрезка к горизонтальной (фронтальной) плоскости проекций.
 Coordinate plane
Coordinate plane Движение в математике
Движение в математике Презентация на тему Приведение дробей к общему знаменателю
Презентация на тему Приведение дробей к общему знаменателю  Множества точек
Множества точек Корреляционный и спектральный анализ случайных процессов
Корреляционный и спектральный анализ случайных процессов Численное интегрирование. Метод средних прямоугольников
Численное интегрирование. Метод средних прямоугольников Сечение поверхности плоскостью
Сечение поверхности плоскостью Логарифмические неравенства
Логарифмические неравенства Треугольник
Треугольник Вписанные и описанные окружности
Вписанные и описанные окружности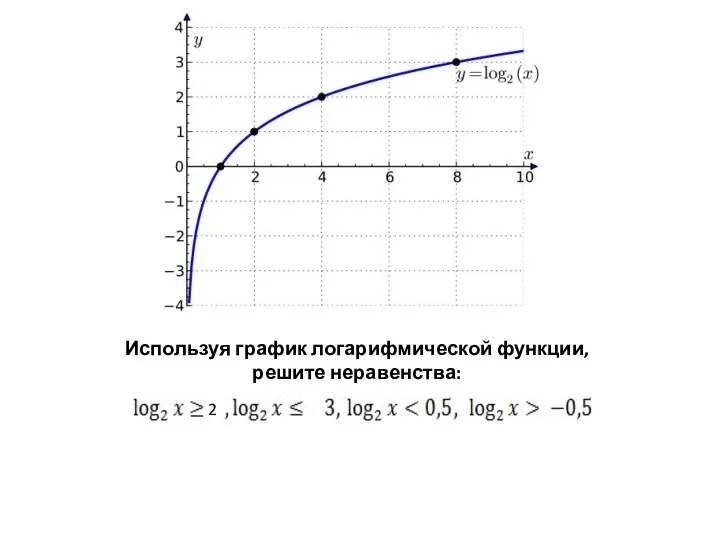 Логарифмические неравенства. устные упражнения
Логарифмические неравенства. устные упражнения Многомерные случайные величины
Многомерные случайные величины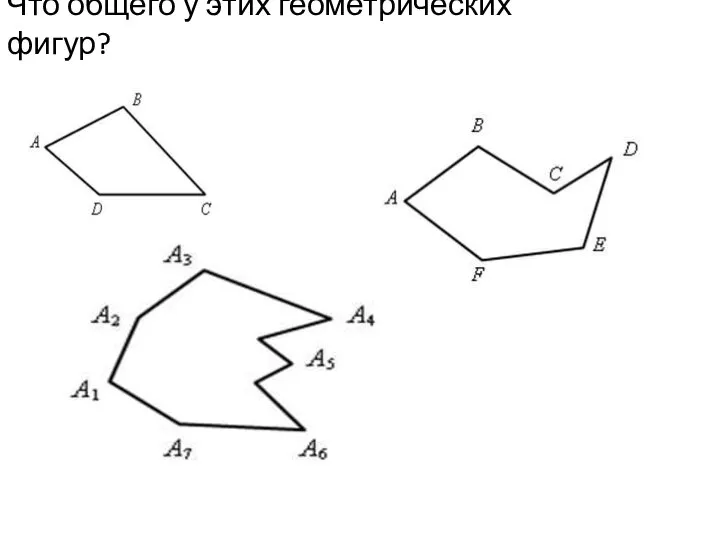 Многоугольники
Многоугольники СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ Счёт до 9. Состав числа 9
Счёт до 9. Состав числа 9 Векторы в пространстве
Векторы в пространстве Урок математики во 2 классе. Повторение
Урок математики во 2 классе. Повторение Заниматика. Миром управляют числа
Заниматика. Миром управляют числа ДПА 11 класс Первообразная и интеграл
ДПА 11 класс Первообразная и интеграл Четырехугольник . Прямоугольник. Квадрат
Четырехугольник . Прямоугольник. Квадрат Презентация на тему Математическое моделирование и проектирование
Презентация на тему Математическое моделирование и проектирование  Тригонометрически уравнения
Тригонометрически уравнения Элементы комбинаторики
Элементы комбинаторики Сравни площади фигур на глаз
Сравни площади фигур на глаз Классическое определение вероятности
Классическое определение вероятности Презентация на тему Геометрия в музыке 11 класс
Презентация на тему Геометрия в музыке 11 класс  Презентация на тему Угол между прямыми
Презентация на тему Угол между прямыми 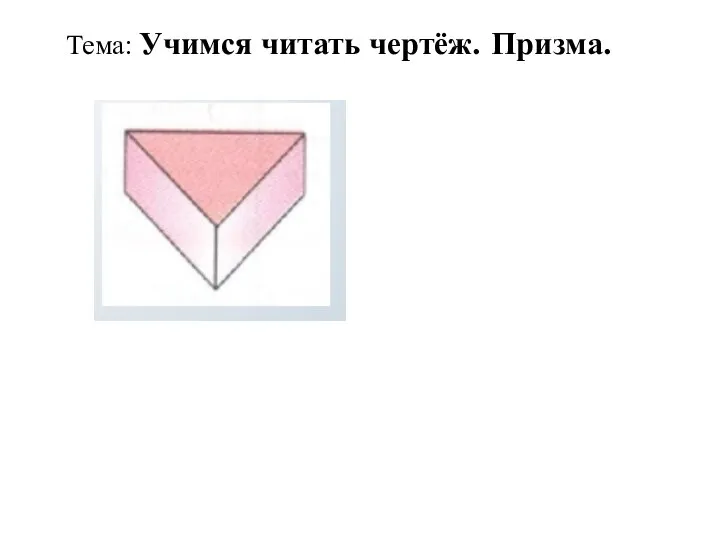 Чертёж призмы
Чертёж призмы