Содержание
- 2. Система линейных уравнений имеет вид Таблица, составленная из коэффициентов при неизвестных, называется матрицей. Для данной системы
- 3. В этой же системе можно выписать в виде матрицы столбец свободных членов Матрица - столбец размера
- 4. Для квадратных матриц можно вычислить определитель. Определитель квадратной матрицы есть некоторое число, которое вычисляется из элементов
- 5. 1. Определитель 1-го порядка равен самому элементу Например: 2. Определитель 2-го порядка находится по правилу Определитель
- 6. Определитель 3-го порядка находится путем разложения определителя по элементам строки или столбца. При этом используется Основное
- 7. Пример вычисления определителя путем разложения по элементам первой строки: Наиболее выгодным является разложение определителя по элементам
- 8. Согласно свойству определителей: Величина определителя не изменится, если к элементам какого-либо ряда прибавить соответствующие элементы другого
- 9. Свойства определителей 1. Постоянный множитель из элементов какого либо ряда можно выносить за знак определителя 2.
- 10. Решение систем методом Крамера С вычислением определителей связан один из методов решения систем линейных уравнений –
- 11. Метод Крамера а) Находим определитель для первого неизвестного, заменяя в главном определителе первый столбец на столбец
- 12. Метод Крамера Для нахождения значений неизвестных используем формулы Крамера Значения неизвестных находятся делением побочных определителей на
- 13. Обратная матрица. Матричные уравнения Обратной матрицей для квадратной матрицы А называется матрица произведение которой на исходную
- 14. Матричные уравнения Матричные уравнения – это уравнения, в которых участвуют как известные матрицы, так и неизвестная
- 15. Схема нахождения обратной матрицы 1) Находится определитель матрицы. Если он отличен от нуля , то обратная
- 16. Нахождение обратной матрицы 2. Найти матрицу, обратную данной 1) Находим определитель матрицы 2) Составляем союзную матрицу
- 17. Решение систем методом Гаусса Метод Гаусса – метод последовательного исключения неизвестных. При решении системы методом Гаусса
- 18. Определение 1. Система линейных уравнений называется совместной, если она имеет решение. Это возможно только в том
- 19. Рассмотрим на примере системы Расширенная матрица – это матрица коэффициентов при неизвестных с добавлением столбца свободных
- 20. Схема решения системы методом Гаусса. Выписываем расширенную матрицу системы и приводим ее к ступенчатому или треугольному
- 21. Для данной ситуации базисными будут неизвестные и 4. Записываем эквивалентную систему, при этом базисные неизвестные остаются
- 23. Скачать презентацию




















 Прямоугольник
Прямоугольник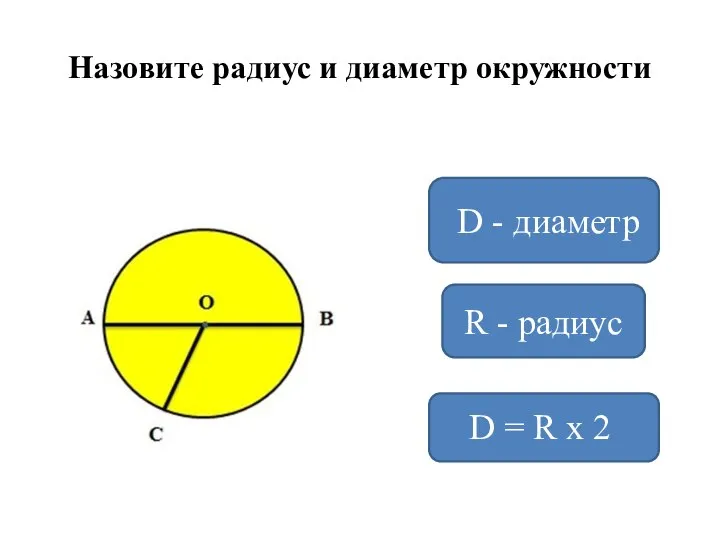 Радиус и диаметр окружности
Радиус и диаметр окружности Сочетания. Задачи
Сочетания. Задачи Единицы стоимости. Рубль, копейка
Единицы стоимости. Рубль, копейка Презентация на тему Теорема Пифагора и её применение
Презентация на тему Теорема Пифагора и её применение  Решение задач на свойства
Решение задач на свойства Приемы письменных вычислений в пределах 1000. 3 класс
Приемы письменных вычислений в пределах 1000. 3 класс Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1
Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1 Нахождение синуса острого угла в прямоугольном треугольнике
Нахождение синуса острого угла в прямоугольном треугольнике Сложение векторов. Сложение сил
Сложение векторов. Сложение сил Обыкновенные дроби. Задания для устного счета. 8 класс
Обыкновенные дроби. Задания для устного счета. 8 класс Презентация на тему Круг. Площадь круга
Презентация на тему Круг. Площадь круга  Вправи на засвоєння таблиці додавання і віднімання числа 7
Вправи на засвоєння таблиці додавання і віднімання числа 7 История развития обыкновенных дробей
История развития обыкновенных дробей Приемы сложения и вычитания в пределах 20 с переходом через десяток
Приемы сложения и вычитания в пределах 20 с переходом через десяток Вывод формулы длины окружности и площади круга
Вывод формулы длины окружности и площади круга Углы с сонаправленными сторонами
Углы с сонаправленными сторонами Степінь з цілим показником
Степінь з цілим показником Решение планиметрических задач
Решение планиметрических задач Презентация на тему Противоположные числа (6 класс)
Презентация на тему Противоположные числа (6 класс)  Сложные проценты. Контрольная
Сложные проценты. Контрольная Презентация на тему Таблицы истинности
Презентация на тему Таблицы истинности  Задачи на движение
Задачи на движение Уравнение окружности
Уравнение окружности Скалярное произведение векторов
Скалярное произведение векторов Калейдоскоп заданий ОГЭ. Математическая игра
Калейдоскоп заданий ОГЭ. Математическая игра Презентация на тему Сочетательное свойство сложения
Презентация на тему Сочетательное свойство сложения  Объемы многогранников
Объемы многогранников