Слайд 2
Система лин. однор. уравнений. Фундаментальная система решений
Общее решение неоднородной системы
Псевдообратные матрицы
Решение

СЛУ с помощью обобщенно обратных матрицы – псевдорешение.
Слайд 3Продолжение. О решении однородной СЛУ

Слайд 4Решение СЛОУ
Всякая система n-мерных векторов, состоящая более чем из n векторов, будет

линейно зависимы.
Вывод: из числа решений однородной системы (1), являющихся n-мерными векторами, можно выбрать конечную максимальную линейно независимую систему векторов. (Максимально в том смысле, что всякое другое решение системы (1) будет линейной комбинацией решений, входящих в эту выбранную систему).
Определение. Всякая максимальная линейно независимая система решений однородной системы (1) называется фундаментальной системой решений.
Если ранг r матрицы из коэффициентов системы линейных однородных уравнений (1) меньше числа неизвестных n, то всякая фундаментальная система решений системы (1) состоит из n-r решений.
Число свободных неизвестных равно n-r
Слайд 5Пример. Фундаментальная система решений СЛОУ

Слайд 8Заключение. О применении СЛУ

Слайд 9Заключение. О применении СЛУ

Слайд 13Основные свойства псевдообратной матрицы

Слайд 14Разложение по матрицам полного ранга

Слайд 15Разложение по матрицам полного ранга

Слайд 16Разложение по матрицам полного ранга

Слайд 18Псевдообратная матрица и аппроксимация

Слайд 23Домашняя задача
[Демидович]
Решить неоднородную систему используя фунд. сист. реш. однородной системы.
![Домашняя задача [Демидович] Решить неоднородную систему используя фунд. сист. реш. однородной системы.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/893672/slide-22.jpg)
Слайд 24Домашняя задача Темы 6.
Задачи из книги Aleskerov_Piontkovski.
Вычислить псевдообратные матрицы.

Слайд 25Домашняя задача Темы 6.
В задаче 7 нужно найти скелетное разложение матрицы A,
т.е.

A=FG.
Задача 8 решается так: сперва находится разложение FG указанной матрицы, а потом применяется теорема 3.





















![Домашняя задача [Демидович] Решить неоднородную систему используя фунд. сист. реш. однородной системы.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/893672/slide-22.jpg)


 Дифференциал функции. Производные высших порядков. Дифференциал функции. Вторая производная и производные высших порядков
Дифференциал функции. Производные высших порядков. Дифференциал функции. Вторая производная и производные высших порядков Основные геометрические фигуры
Основные геометрические фигуры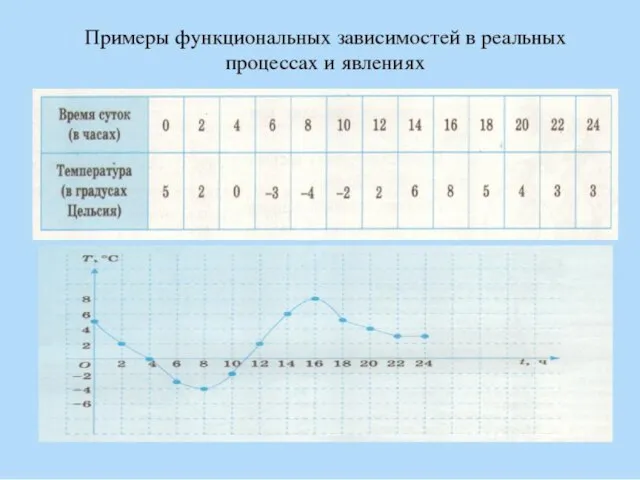 График функции. Примеры
График функции. Примеры Вычисления. 5 класс
Вычисления. 5 класс Математический квест (8 класс)
Математический квест (8 класс) Системы линейных неравенств
Системы линейных неравенств Презентация на тему Исследование функции с помощью производной
Презентация на тему Исследование функции с помощью производной  Степени с рациональными показателями, их свойства
Степени с рациональными показателями, их свойства Геометрическая прогрессия
Геометрическая прогрессия Иррациональные неравенства
Иррациональные неравенства Контрольная
Контрольная Требования к оформлению печатных проектно-исследовательских работ
Требования к оформлению печатных проектно-исследовательских работ Формулы тангенсов и котангенсов
Формулы тангенсов и котангенсов Сфера, описанная вокруг многогранника
Сфера, описанная вокруг многогранника Числа вокруг нас
Числа вокруг нас Формирование элементарных математических представлений
Формирование элементарных математических представлений Решение выражений и уравнений
Решение выражений и уравнений Свойства функций
Свойства функций Площа криволінійної трапеції
Площа криволінійної трапеції Шар и сфера
Шар и сфера Развернутый план-конспект открытого урока по математике ГОУ НПО ПЛ №35 Саратов,2011
Развернутый план-конспект открытого урока по математике ГОУ НПО ПЛ №35 Саратов,2011 Площадь полной поверхности призмы
Площадь полной поверхности призмы Численные решения обыкновенных дифференциальных уравнений (ОДУ)
Численные решения обыкновенных дифференциальных уравнений (ОДУ) Пропорции. Задачи
Пропорции. Задачи Деление круглых сотен на число 100
Деление круглых сотен на число 100 Экстремум функции с единственной критической точкой
Экстремум функции с единственной критической точкой Решение различных задач с помощью систем уравнений второй степени
Решение различных задач с помощью систем уравнений второй степени Числовая окружность
Числовая окружность