- Главная
- Математика
- Сравнение бесконечно малых

Содержание
Слайд 2Пусть α ( x ) и β ( x ) б.м.ф. при
Пусть α ( x ) и β ( x ) б.м.ф. при

§ 7. Сравнение бесконечно малых
Опр. 33. α ( x ) и β ( x ) – б.м. одного порядка малости, если
Опр. 34. α ( x ) – б.м. высшего порядка малости относительно β ( x ), если
Опр. 35. α ( x ) – б.м. низшего порядка малости относительно β ( x ), если
пишут: α ( x ) = o (β ( x )) или α ( x ) << β ( x )
пишут: β ( x ) = o (α ( x )) или β ( x ) << α ( x )
Слайд 3Опр. 37. Пусть α ( x ) и β ( x )
Опр. 37. Пусть α ( x ) и β ( x )

α ( x ) называется б.м. k - го порядка малости относительно β ( x ), если
Число k называется порядком малости
α и β одного порядком малости
Теорема 6. Произведение б.м. α ( x ) и β ( x ) есть б.м. высшего порядка малости по сравнению с каждым из сомножителей.
α ( x ) β ( x ) << α ( x )
Слайд 4Опр. 38. Пусть f ( x ) и g ( x )
Опр. 38. Пусть f ( x ) и g ( x )

Сравнение бесконечно больших функций. Эквивалентные бесконечно большие
1. Б.б. f ( x ) и g ( x ) при x→x0 называются б.б. одного порядка роста, если
2. Б.б. f ( x ) – низшего порядка роста относительно g ( x ), если
3. Б.б. f ( x ) – б.б. высшего порядка роста относительно g ( x ), если
пишут: f ( x ) << g ( x )
пишут: f ( x ) >> g ( x )
4. Б.б. f ( x ) и g ( x ) при x→x0 называются эквивалентными, если
пишут: f ( x ) ~ g ( x )
Слайд 5Свойства
1. Сумма б.б. величин разных порядков эквивалентна слагаемому высшего порядка роста.
2.
Свойства
1. Сумма б.б. величин разных порядков эквивалентна слагаемому высшего порядка роста.
2.

3. Произведение двух б.б.ф. имеет высший порядок роста относительно каждого из сомножителей
 Аналоги теореми порівняння Колмогорова та їх застосування
Аналоги теореми порівняння Колмогорова та їх застосування Бутылка Клейна
Бутылка Клейна Устный счет
Устный счет Применение производной к исследованию функции и построению графика функции
Применение производной к исследованию функции и построению графика функции Прямоугольный параллелепипед
Прямоугольный параллелепипед Кругові приклади
Кругові приклади Сложение и вычитание вида +1 и -1
Сложение и вычитание вида +1 и -1 Состав чисел в пределах 10. Закрепление пройденного
Состав чисел в пределах 10. Закрепление пройденного Геометрические фигуры (открытый урок - игра Поле чудес)
Геометрические фигуры (открытый урок - игра Поле чудес) Сумма углов в треугольнике
Сумма углов в треугольнике Приближение десятичных дробей
Приближение десятичных дробей Порядок действий в примерах (для младших школьников)
Порядок действий в примерах (для младших школьников) Логика предикатов
Логика предикатов Готовимся к ЕГЭ. Базовый уровень
Готовимся к ЕГЭ. Базовый уровень Аппликации из геометрических фигур
Аппликации из геометрических фигур Треугольники. Решение задач
Треугольники. Решение задач Обработка результатов измерения отклонений от круглости
Обработка результатов измерения отклонений от круглости Углы, связанные с окружностью
Углы, связанные с окружностью Величины
Величины Презентация на тему Число и цифра 4
Презентация на тему Число и цифра 4  Выберите чётные числа (триггеры)
Выберите чётные числа (триггеры) Подготовка к ОГЭ, 9 класс, геометрия
Подготовка к ОГЭ, 9 класс, геометрия Моделирование вероятности столкновения судов
Моделирование вероятности столкновения судов 2.1._-_
2.1._-_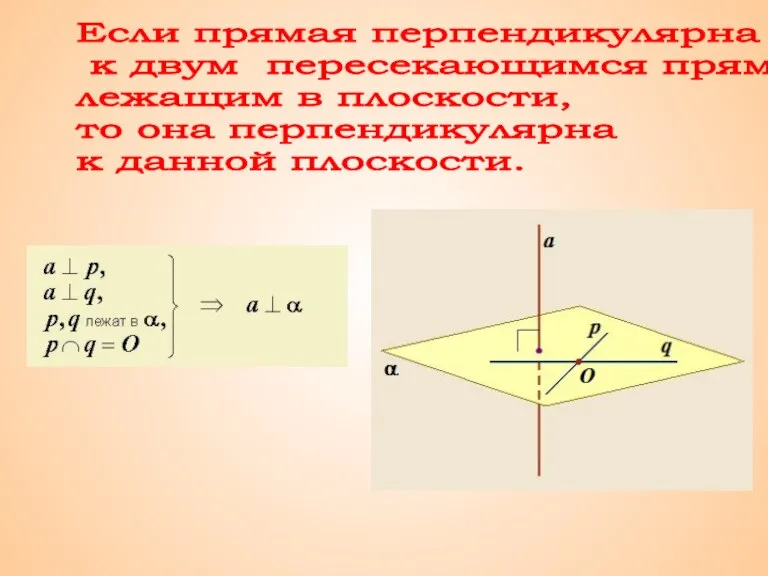 Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Основы метрологического обеспечения
Основы метрологического обеспечения Смежные и вертикальные углы
Смежные и вертикальные углы