Содержание
- 2. Определения. 1.Секущая плоскость тетраэдра(параллелепипеда)-это любая плоскость, по обе стороны от которой имеются точки данного тетраэдра (параллелепипеда).
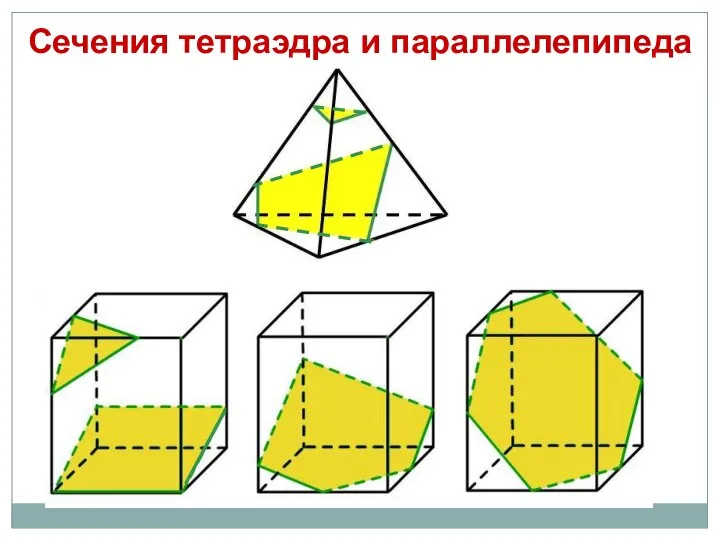
- 3. Сечения тетраэдра и параллелепипеда
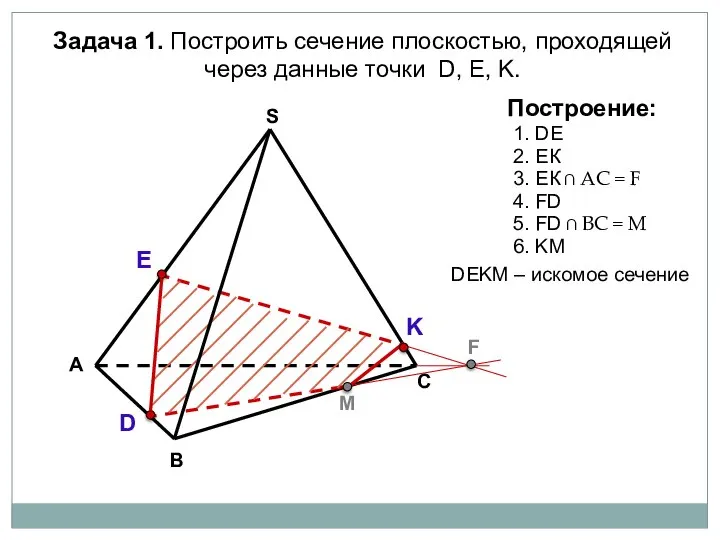
- 4. А В С S Задача 1. Построить сечение плоскостью, проходящей через данные точки D, Е, K.
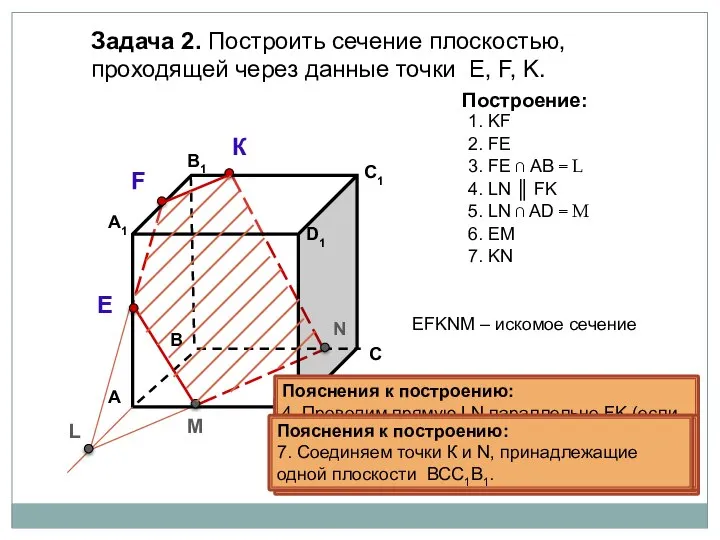
- 5. Пояснения к построению: 1. Соединяем точки K и F, принадлежащие одной плоскости А1В1С1D1. Задача 2. Построить
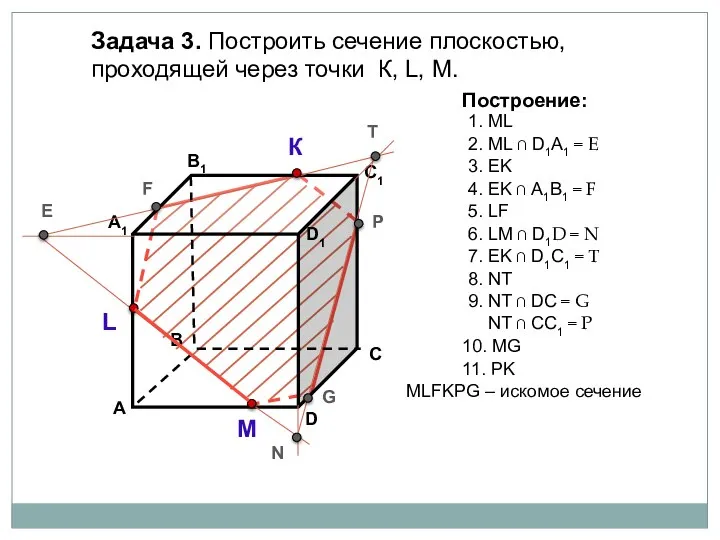
- 6. Задача 3. Построить сечение плоскостью, проходящей через точки К, L, М. К L М Построение: 1.
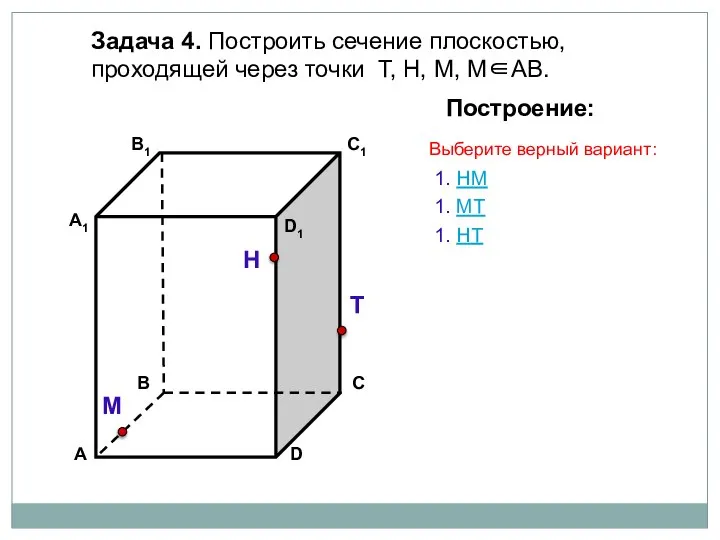
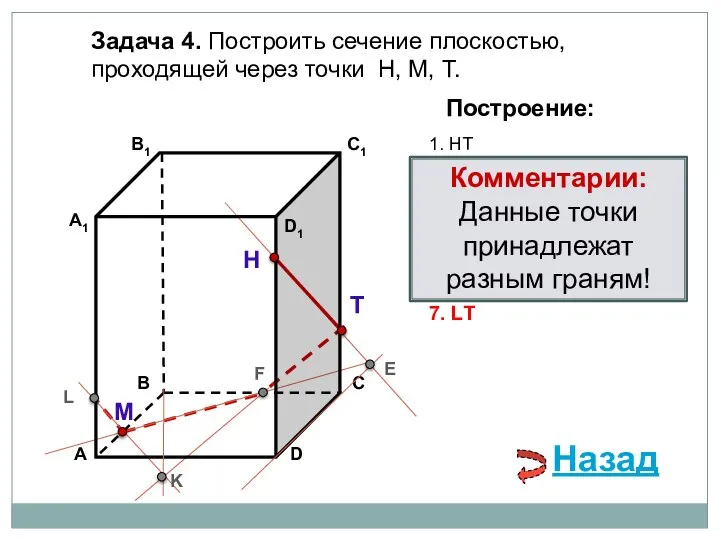
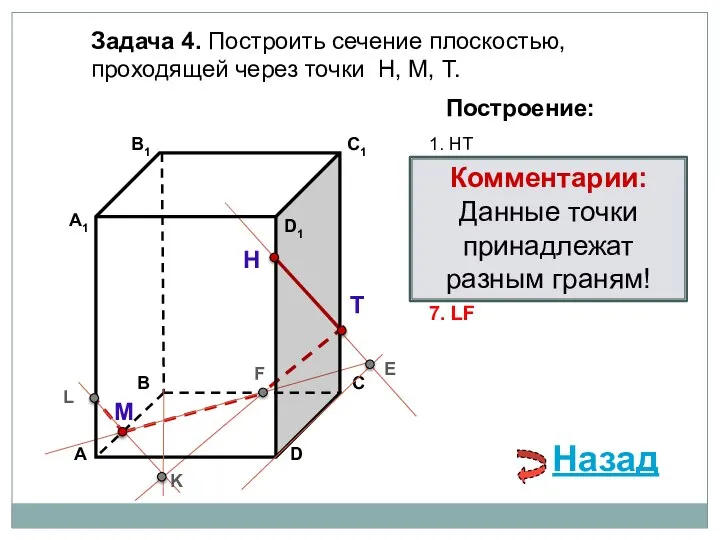
- 7. Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
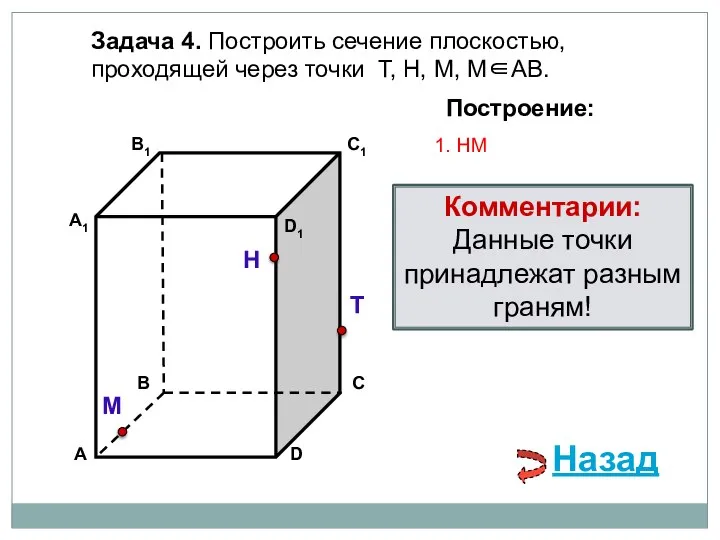
- 8. Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
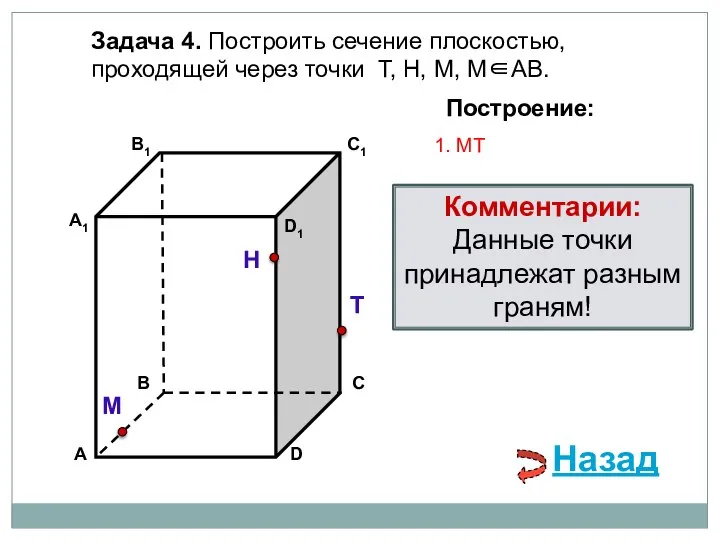
- 9. Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
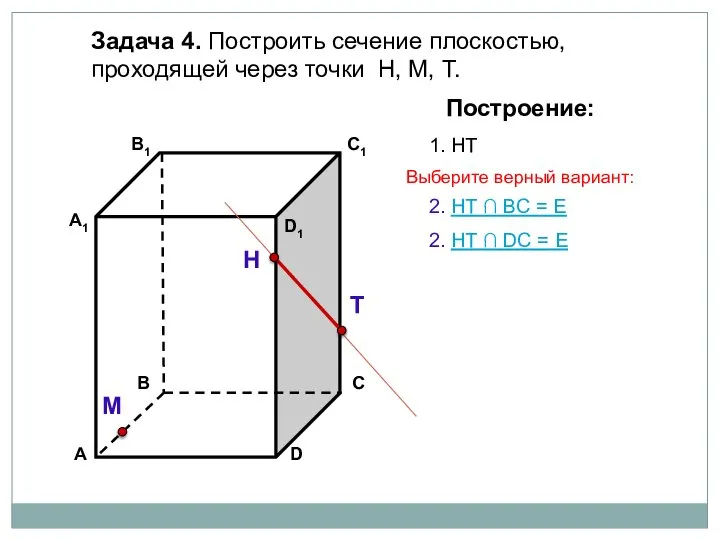
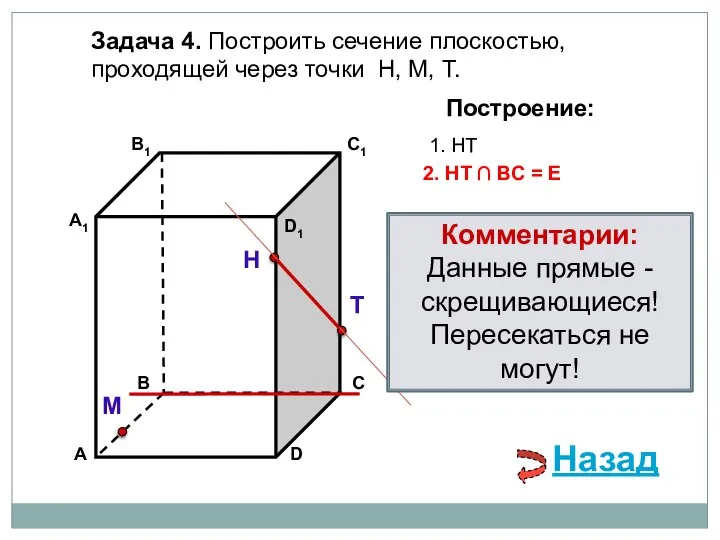
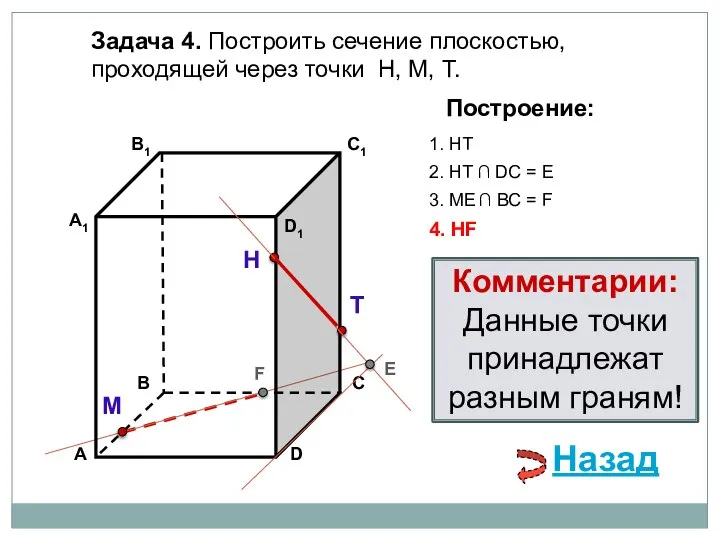
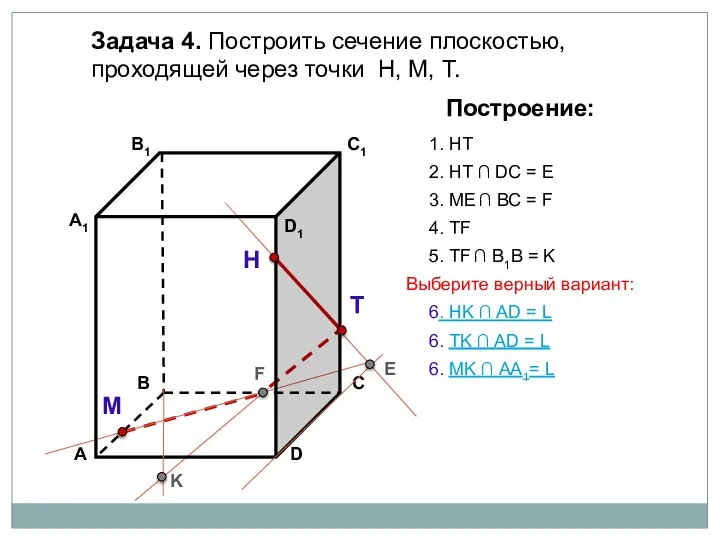
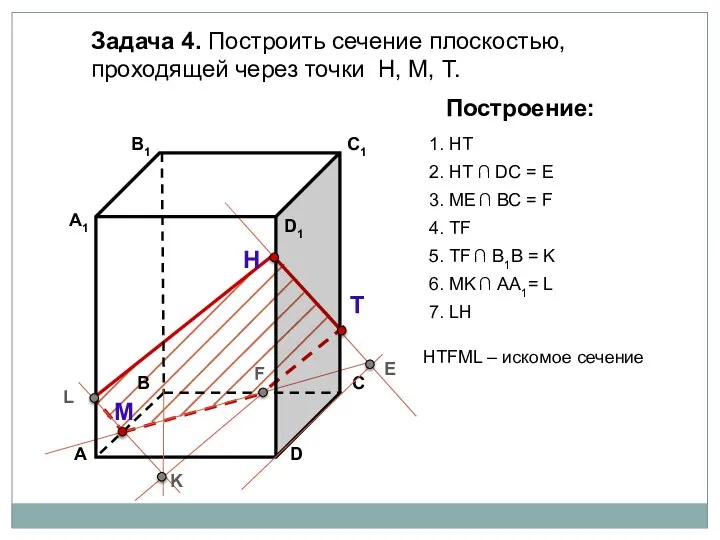
- 10. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 11. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
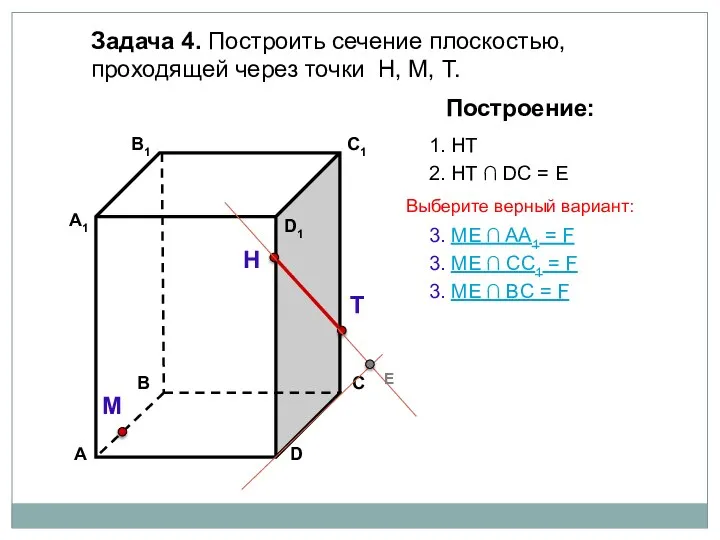
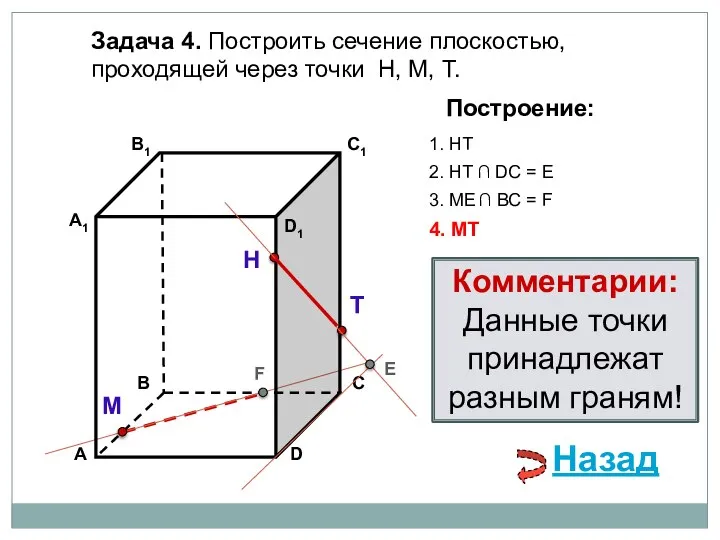
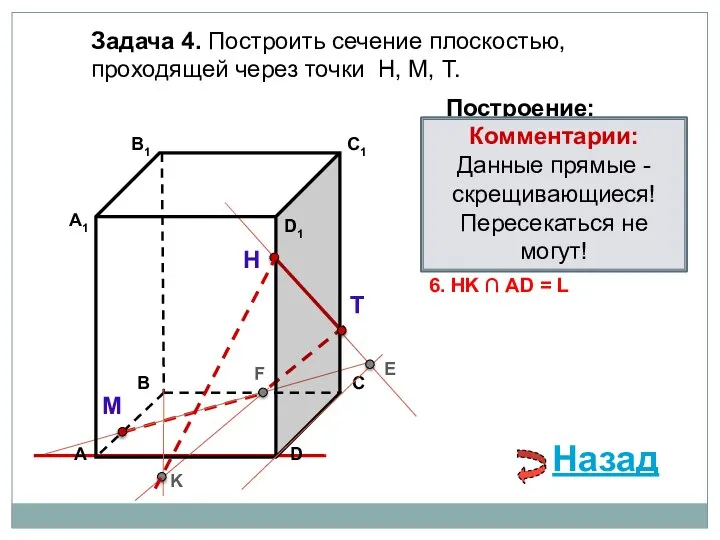
- 12. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 13. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
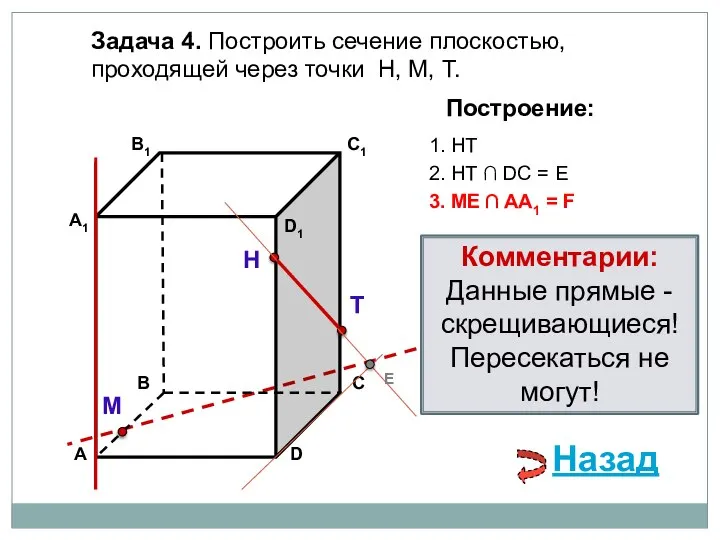
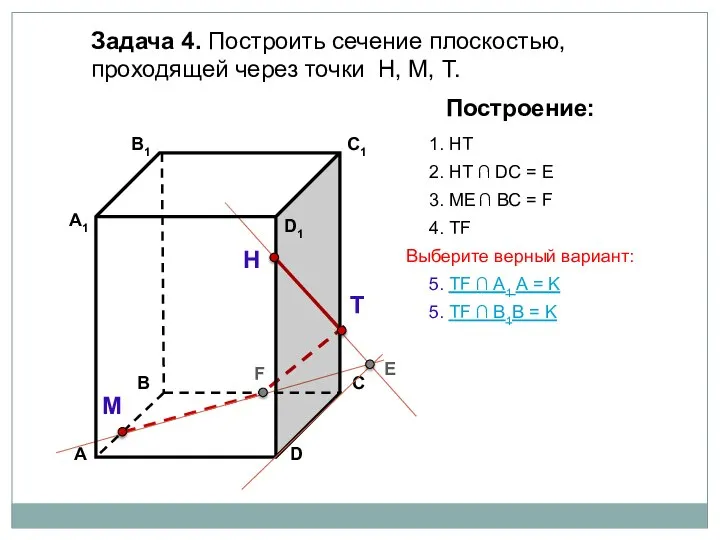
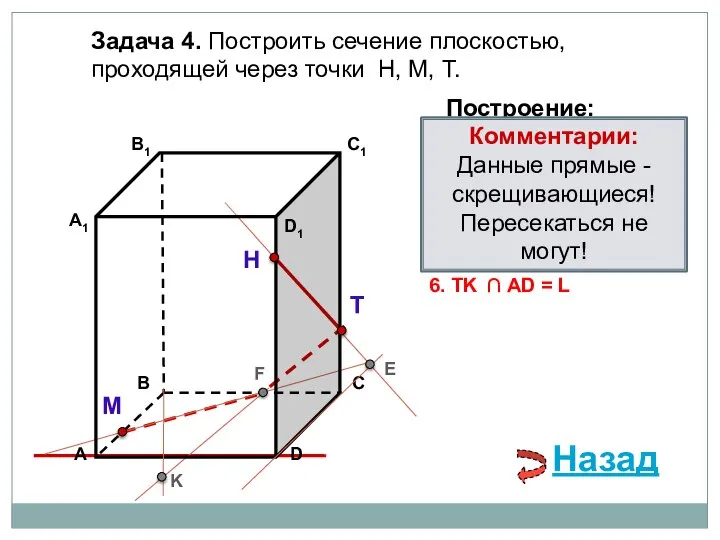
- 14. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 15. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
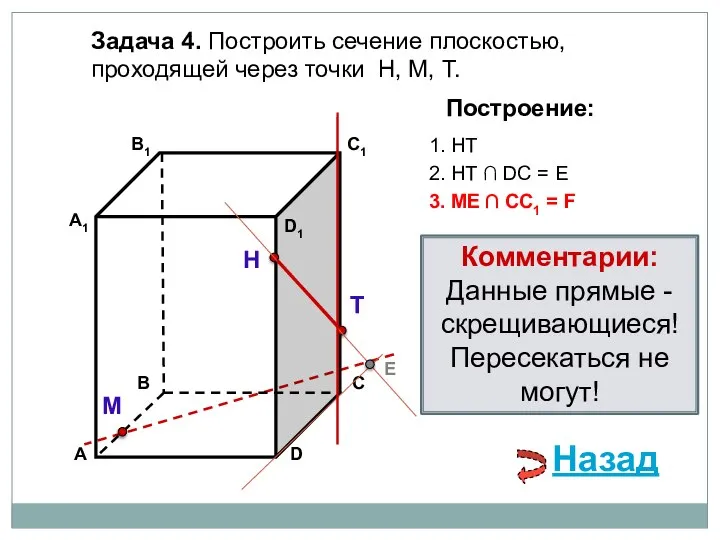
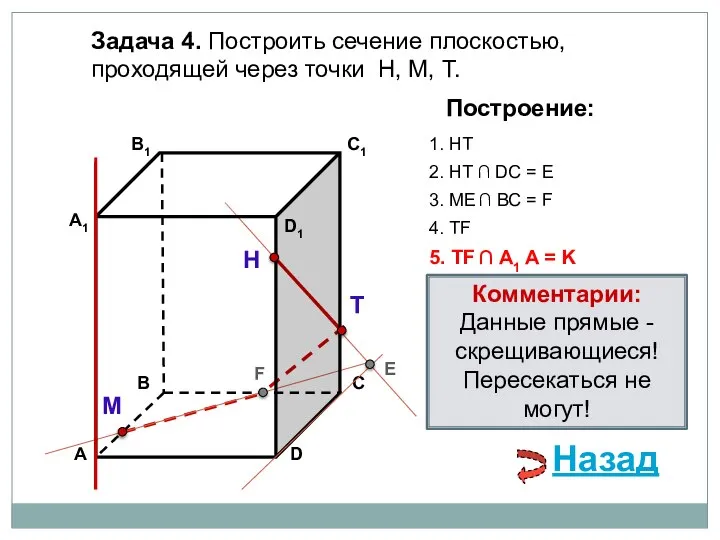
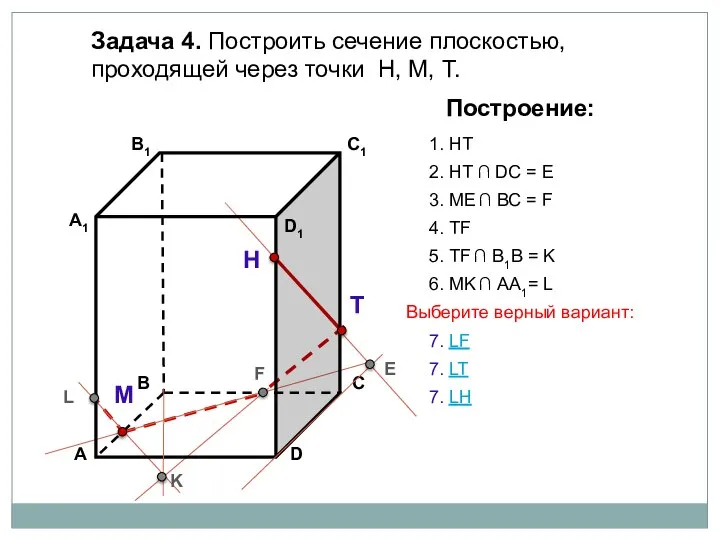
- 16. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 17. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 18. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 19. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 20. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 21. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 22. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 23. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 24. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 25. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 26. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
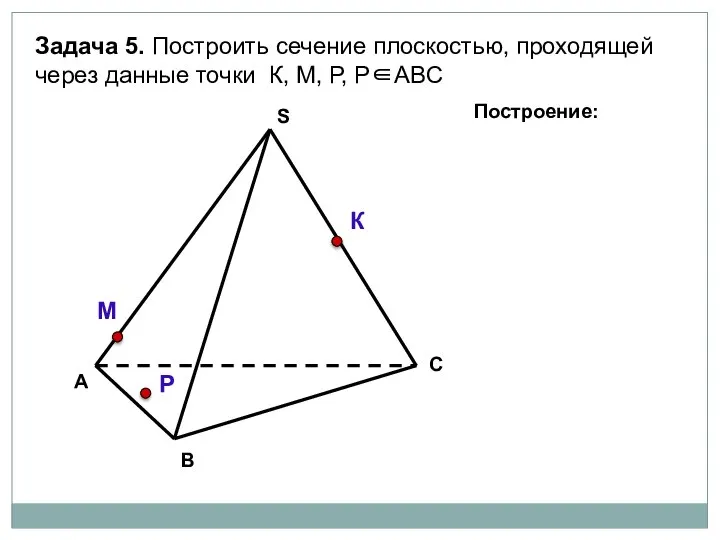
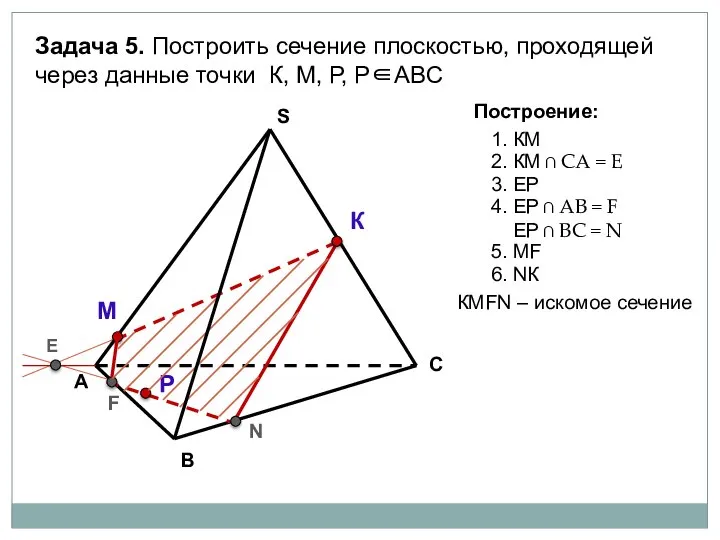
- 27. А В С S Задача 5. Построить сечение плоскостью, проходящей через данные точки К, М, Р,
- 28. А В С S Задача 5. Построить сечение плоскостью, проходящей через данные точки К, М, Р,
- 30. Скачать презентацию


 Разработка обучающей программы по нахождению элементов треугольника
Разработка обучающей программы по нахождению элементов треугольника Свойство углов треугольника
Свойство углов треугольника 04.17.21.00[1]
04.17.21.00[1] Теорема Пифагора
Теорема Пифагора Презентация на тему Учим состав числа от 5 до 10
Презентация на тему Учим состав числа от 5 до 10  Повтарение по математике. Уравнение
Повтарение по математике. Уравнение Второй и третий признаки подобия треугольников
Второй и третий признаки подобия треугольников Разложение функций в степенные ряды
Разложение функций в степенные ряды ВПР вариант 16 № 11. Решение трудной задачи
ВПР вариант 16 № 11. Решение трудной задачи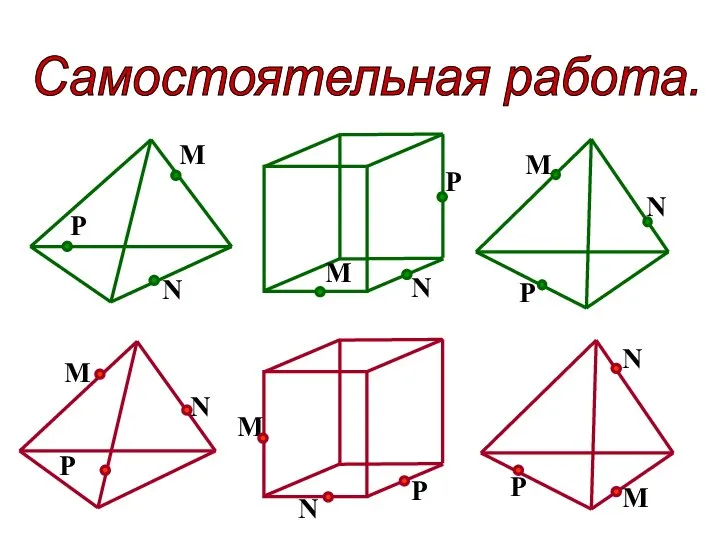 Построение сечений многогранников
Построение сечений многогранников Уравнение окружности. 2 урок
Уравнение окружности. 2 урок Преобразование выражений содержащих степень с отрицательным целым показателем
Преобразование выражений содержащих степень с отрицательным целым показателем 5.0 Простейшие задачи в координатах
5.0 Простейшие задачи в координатах Сумма углов треугольника
Сумма углов треугольника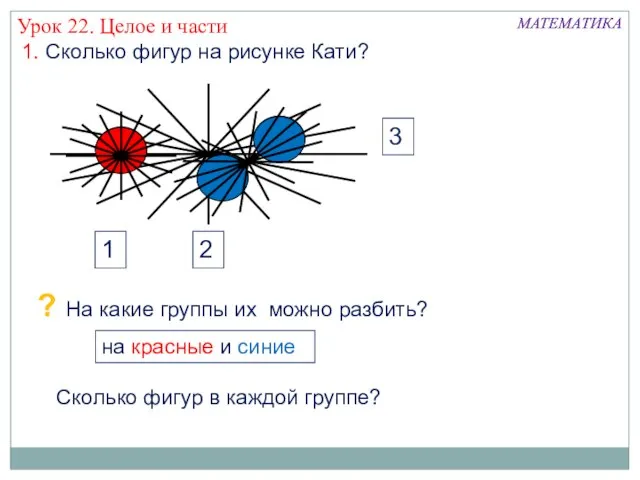 Целое и части
Целое и части Системы счисления
Системы счисления Презентация на тему Число и цифра 2 (1 класс)
Презентация на тему Число и цифра 2 (1 класс)  Уравнение окружности
Уравнение окружности Введение в аналитическую геометрию. Векторы на плоскости и в пространстве
Введение в аналитическую геометрию. Векторы на плоскости и в пространстве Сфера, описанная вокруг многогранника
Сфера, описанная вокруг многогранника Фракталы
Фракталы Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Неопределенный интеграл
Неопределенный интеграл Предел_посл_1
Предел_посл_1 Презентация на тему Вычисление объемов пространственных тел
Презентация на тему Вычисление объемов пространственных тел  Арифметическая прогрессия. Обобщающий урок
Арифметическая прогрессия. Обобщающий урок Одночлен и его стандартный вид
Одночлен и его стандартный вид Деление одночлена на одночлен. Урок 50. 7 класс
Деление одночлена на одночлен. Урок 50. 7 класс