Содержание
- 2. 2 1. Модель размножения и гибели 1.1 Граф модели размножения и гибели Имея в распоряжении размеченный
- 3. 3 1. Модель размножения и гибели 1.1 Граф модели размножения и гибели Особенность этого графа в
- 4. 4 1. Модель размножения и гибели 1.2 Дифференциальные уравнения Колмогорова Составим дифференциальные уравнения Колмогорова для всех
- 5. 5 1. Модель размножения и гибели 1.2 Дифференциальные уравнения Колмогорова Вероятность события А найдем по теореме
- 6. 6 1. Модель размножения и гибели 1.2 Дифференциальные уравнения Колмогорова Найдем вероятность события p(B). Вероятность того,
- 7. 7 1. Модель размножения и гибели 1.2 Дифференциальные уравнения Колмогорова Суммируя вероятности событий А и В,
- 8. 8 1. Модель размножения и гибели 1.2 Дифференциальные уравнения Колмогорова Аналогично, могут быть получены дифференциальные уравнения
- 9. 9 1. Модель размножения и гибели 1.3 Финальные стационарные уравнения Колмогорова Вначале, после включения рассматриваемой системы
- 10. 10 1. Модель размножения и гибели 1.3 Финальные стационарные уравнения Колмогорова Заменим в системе обыкновенных дифференциальных
- 11. 11 1. Модель размножения и гибели 1.3 Финальные стационарные уравнения Колмогорова Разрешим полученную систему относительно неизвестных
- 12. 12 1. Модель размножения и гибели 1.3 Финальные стационарные уравнения Колмогорова Итоговая система преобразованных уравнений имеет
- 13. 13 1. Модель размножения и гибели 1.3 Финальные стационарные уравнения Колмогорова В числителе стоит произведение всех
- 14. 14 2. Модель вычислительной системы в виде одноканальной СМО с очередью Характеристики вычислительной системы Рассмотрим систему
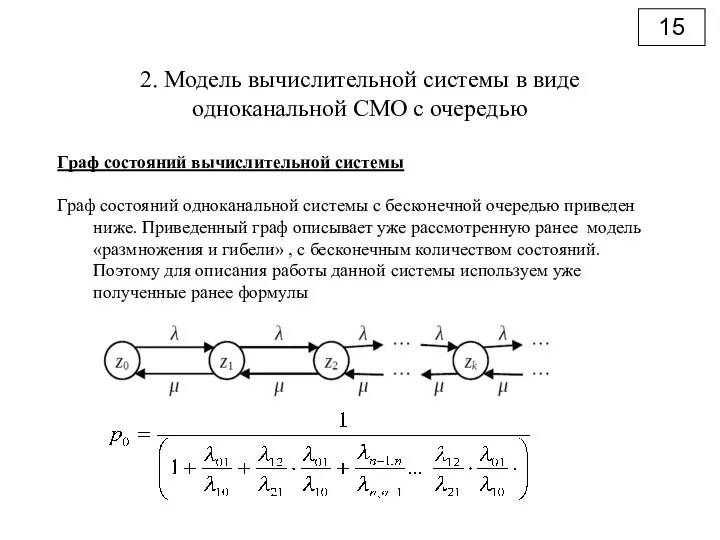
- 15. 15 2. Модель вычислительной системы в виде одноканальной СМО с очередью Граф состояний вычислительной системы Граф
- 16. 16 Если обозначить λ/μ=ρ, то получим: 2. Модель вычислительной системы в виде одноканальной СМО с очередью
- 17. 17 2. Модель вычислительной системы в виде одноканальной СМО с очередью Коэффициент загрузки Из математики известно,
- 18. 18 2. Модель вычислительной системы в виде одноканальной СМО с очередью Коэффициент загрузки Финальные вероятности, как
- 19. 19 2. Модель вычислительной системы в виде одноканальной СМО с очередью Среднее число заявок в системе
- 20. 20 2. Модель вычислительной системы в виде одноканальной СМО с очередью Среднее число заявок в системе
- 21. 21 2. Модель вычислительной системы в виде одноканальной СМО с очередью Длина очереди Средняя длина очереди
- 22. 2. Модель вычислительной системы в виде одноканальной СМО с очередью 22 Среднее время пребывания заявки в
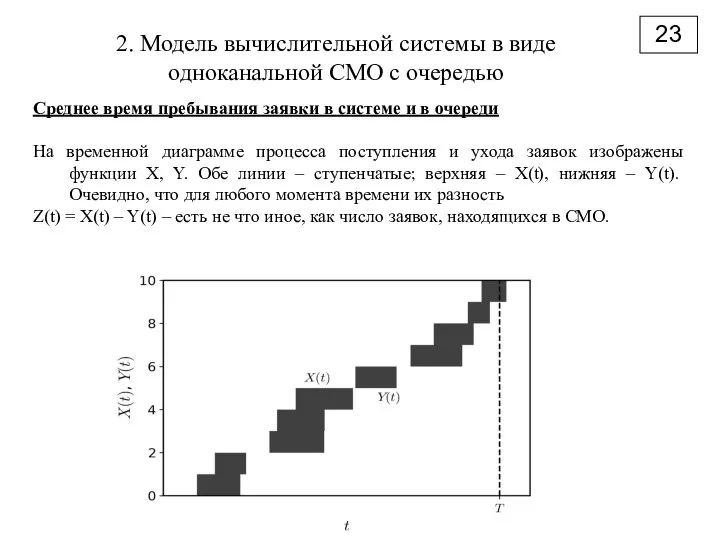
- 23. 2. Модель вычислительной системы в виде одноканальной СМО с очередью 23 Среднее время пребывания заявки в
- 24. 2. Модель вычислительной системы в виде одноканальной СМО с очередью 24 Среднее время пребывания заявки в
- 25. 2. Модель вычислительной системы в виде одноканальной СМО с очередью 25 Среднее время пребывания заявки в
- 26. 2. Модель вычислительной системы в виде одноканальной СМО с очередью 26 Среднее время пребывания заявки в
- 27. 2. Модель вычислительной системы в виде одноканальной СМО с очередью 27 Среднее время пребывания заявки в
- 29. Скачать презентацию
























 Презентация на тему Решение задач различными способами
Презентация на тему Решение задач различными способами  Математический анализ
Математический анализ Статистика, часть 6. Условные обозначения
Статистика, часть 6. Условные обозначения Построение сечений многогранников
Построение сечений многогранников Фундаментальная система решений (ФСР)
Фундаментальная система решений (ФСР) Интерполяционный многочлен Ньютона
Интерполяционный многочлен Ньютона Векторы в пространстве
Векторы в пространстве График кусочно гладкой функции
График кусочно гладкой функции Построение прямоугольника от двух прямых углов. Прямоугольная коробка
Построение прямоугольника от двух прямых углов. Прямоугольная коробка Определители 2-го и 3-го порядков решение систем линейных уравнений с помощью определителей
Определители 2-го и 3-го порядков решение систем линейных уравнений с помощью определителей Презентация по математике "Кафе «Математики»" -
Презентация по математике "Кафе «Математики»" -  Дифференциальные операции первого порядка
Дифференциальные операции первого порядка Практическое занятие Числа
Практическое занятие Числа Тема: 14 -
Тема: 14 - Разные задачи (6 класс)
Разные задачи (6 класс) Решение транспортных задач линейного программирования
Решение транспортных задач линейного программирования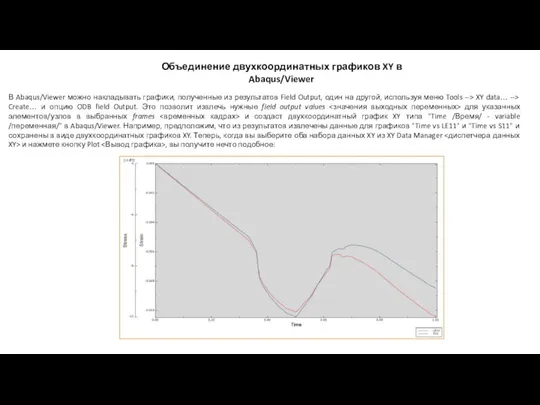 Объединение двухкоординатных графиков XY в Abaqus/Viewer
Объединение двухкоординатных графиков XY в Abaqus/Viewer Презентация на тему Треугольники
Презентация на тему Треугольники  Построение сечений многогранников
Построение сечений многогранников Число и цифра 0 (1 класс)
Число и цифра 0 (1 класс) Параллельность прямых
Параллельность прямых Решение систем уравнений и неравенств графическим способом
Решение систем уравнений и неравенств графическим способом Могла ли математика спасти Пахома, или Площадь
Могла ли математика спасти Пахома, или Площадь арифметическая прогрессия. Решение задач. 9 класс
арифметическая прогрессия. Решение задач. 9 класс Преобразование графиков
Преобразование графиков Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях
Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях Правильные многогранники
Правильные многогранники Магический квадрат. 2 класс
Магический квадрат. 2 класс