Содержание
- 2. Понятие Объема Объем геометрического тела – та часть пространства, которую занимает данное тело. Объем измеряется в
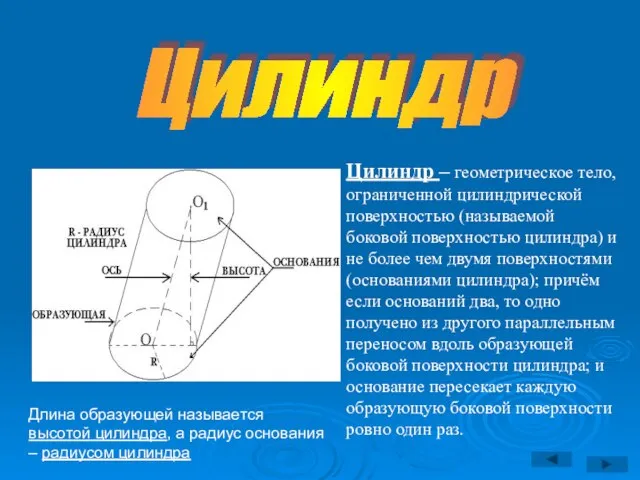
- 3. Цилиндр Цилиндр – геометрическое тело, ограниченной цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем
- 4. Объем цилиндра Объем цилиндра равен произведению площади основания на высоту: Для доказательства впишем в данный цилиндр
- 5. КОНУС Геометрическое тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Образующая – это
- 6. Объем конуса Объем конуса равен одной трети произведения площади основания на высоту: Доказательство:
- 7. Усеченный конус Возьмем произвольный конус и проведем секущую плоскость, перпендикулярно к его оси. Эта плоскость пересекается
- 8. Объем усеченного конуса Объем V усеченного конуса, высота которого равна h, а площади основания равны S
- 9. Доказательство: Объем усеченного конуса может быть найден как разность объемов конусов с радиусами оснований R и
- 11. Скачать презентацию







 Скользящее среднее
Скользящее среднее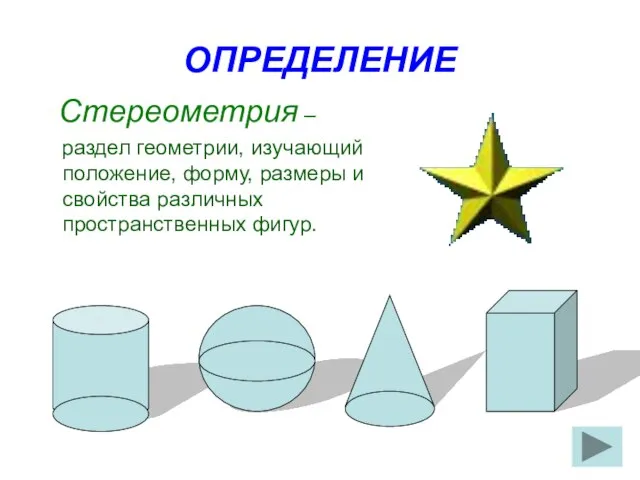 Введение в стереометрию
Введение в стереометрию Уравнения, приводимые к квадратным
Уравнения, приводимые к квадратным Интересные факты про математику
Интересные факты про математику Презентация на тему Уравнения
Презентация на тему Уравнения  Решение задач на проценты. 6 класс. Урок 1
Решение задач на проценты. 6 класс. Урок 1 Показательное уравнение
Показательное уравнение Занимательная математика
Занимательная математика Математическая индукция
Математическая индукция Таблицs истинности
Таблицs истинности Описание линейной дискретной системы в частотной области (ЛДС). Частотные характеристики ЛДС
Описание линейной дискретной системы в частотной области (ЛДС). Частотные характеристики ЛДС Внеаудиторная самостоятельная работа по теме: Функция, ее свойства и график
Внеаудиторная самостоятельная работа по теме: Функция, ее свойства и график Взаимное расположение прямой и окружности, двух окружностей
Взаимное расположение прямой и окружности, двух окружностей Презентация на тему Математика - царица наук
Презентация на тему Математика - царица наук  Вычисление дробей
Вычисление дробей Призма. Дисперсия света в призме
Призма. Дисперсия света в призме Параллельные прямые. Свойства и признаки параллельных прямых
Параллельные прямые. Свойства и признаки параллельных прямых Индивидуальное задание №8. Построение линии пересечения тора и конуса
Индивидуальное задание №8. Построение линии пересечения тора и конуса Тригонометрические уравнения
Тригонометрические уравнения Площадь многоугольника
Площадь многоугольника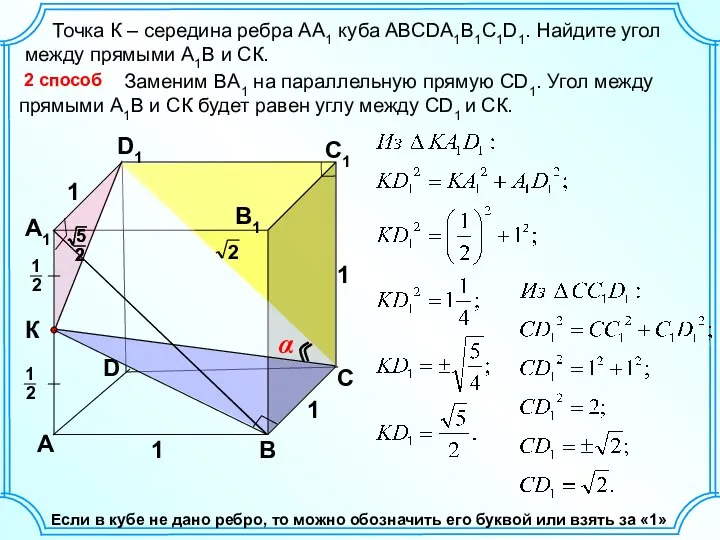 Решение задач
Решение задач Производная вокруг нас
Производная вокруг нас Координаты вектора. Параллелограмм
Координаты вектора. Параллелограмм Прикладна математика
Прикладна математика Учимся складывать столбиком
Учимся складывать столбиком Вычисления вида 32 + 8, 40 – 8
Вычисления вида 32 + 8, 40 – 8 Презентация на тему Логарифмическая функция в уравнениях
Презентация на тему Логарифмическая функция в уравнениях  Линейное уравнение с двумя переменными и его график. 7 класс
Линейное уравнение с двумя переменными и его график. 7 класс