Содержание
- 2. Определение: Неравенства вида ax>b, ax
- 3. Пример 1: (m-1)x Решение: m=1 – контрольное значение
- 4. Пример 2: Решить неравенство при всех значениях параметра a: a(3x-5) Решение: Приведем к линейному виду: 3ax-5a
- 5. Пример 3: Чему равно значение переменной при различных значениях параметра: Решение: Приведем к линейному виду:
- 7. Пример 4: Найти все значения переменной относительно параметра а: Решение: Приведем к линейному виду ax=b:
- 9. Пример 5: Решить неравенство: Решение:
- 10. Пример 6: При каких значениях k неравенство (k-1)x+2k+1>0 (1) верно при всех значениях x, удовлетворяющих условию
- 12. Скачать презентацию




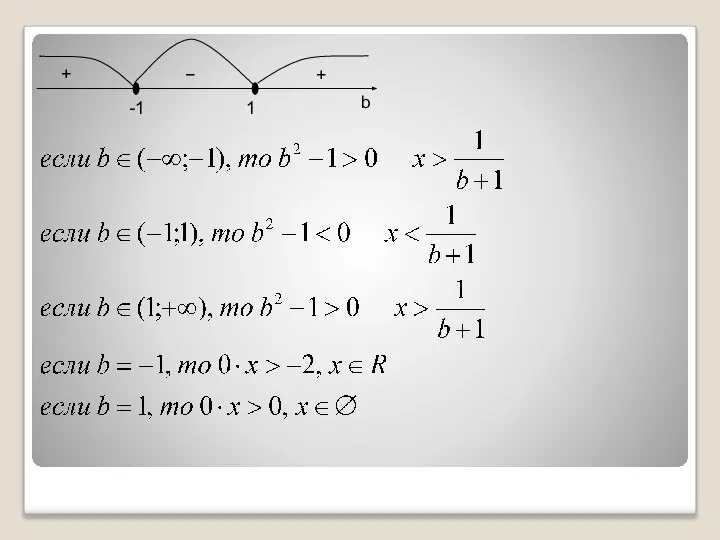

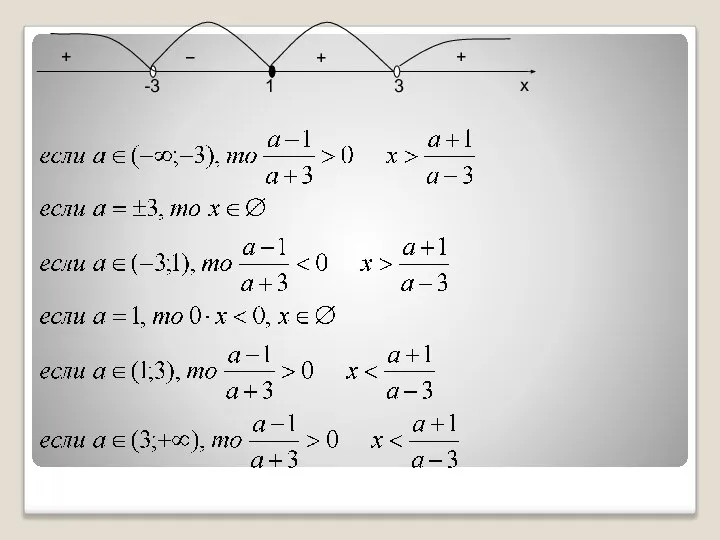


 Применение производной в различных науках
Применение производной в различных науках Корни натуральной степени из числа и их свойства
Корни натуральной степени из числа и их свойства Декартова система координат
Декартова система координат В стране занимательной Математики
В стране занимательной Математики Многогранники на службе у человека
Многогранники на службе у человека Аксиомы стереометрии
Аксиомы стереометрии Методика прикладных вычислений в конечных полях
Методика прикладных вычислений в конечных полях Многогранники в архитектуре
Многогранники в архитектуре Геометрия вокруг нас
Геометрия вокруг нас Презентация на тему Сложение и вычитание круглых десятков и однозначных чисел
Презентация на тему Сложение и вычитание круглых десятков и однозначных чисел  Теорема Пифагора
Теорема Пифагора Одночлен. Умножение
Одночлен. Умножение Логарифм числа и его свойства
Логарифм числа и его свойства электронный учебник по интеллектике в 5 классе. знакомство с вероятностью
электронный учебник по интеллектике в 5 классе. знакомство с вероятностью Неопределённый и определённый интеграл
Неопределённый и определённый интеграл Мультипликативная система индексов
Мультипликативная система индексов Циклоида, эпициклоида
Циклоида, эпициклоида Свойства и графики тригонометрических функций
Свойства и графики тригонометрических функций Экстремумы (1)
Экстремумы (1) Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -
Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -  Степень с натуральным показателем
Степень с натуральным показателем Геймификация образовательного процесса на уроках математики с использованием двигательной активности
Геймификация образовательного процесса на уроках математики с использованием двигательной активности Графический диктант Раскрытие скобок
Графический диктант Раскрытие скобок Что будет со мной, если буду питаться, как Дюймовочка?
Что будет со мной, если буду питаться, как Дюймовочка? Математическая викторина
Математическая викторина Итоговая диагностика. Математическая вертикаль. 8 класс
Итоговая диагностика. Математическая вертикаль. 8 класс Множества. (Задачи)
Множества. (Задачи) Таблица умножения и деления с числом 7
Таблица умножения и деления с числом 7