Физическое и математическое моделирование

УЧЕБНЫЕ ВОПРОСЫ
1. Физическое моделирование.
2. Математическое моделирование.
ЛИТЕРАТУРА:
Советов Б.Я., Яковлев С.А. Моделирование систем. – М.: Высшая школа, 2007 г., с. 31…38.
3. Прямые и обратные задачи математического моделирова­ния.

1. Физическое моделирование
Физическое моделирование – это вид моделирования, который состоит в замене изучения некоторого объекта или явления экспериментальным исследованием его модели, имеющей ту же физическую природу.
В основе физического моделирования лежат теория подобия и анализ размерностей.
Теория подобия – это учение об условиях подобия физических явлений. Теория подобия опирается на учение о размерностях физических величин и служит основой моделирования физического. Предметом теории подобия является установление подобия критериев различных физических явлений и изучение с помощью этих критериев свойств самих явлений.

Физические явления, процессы или системы подобны, если в сходственные моменты времени в сходственных точках пространства значения переменных величин, характеризующих состояние одной системы, пропорциональны соответствующим величинам другой системы. Коэффициенты пропорциональности для каждой из величин называется коэффициентом подобия.

Безразмерные комбинации, составленные из определяющих параметров рассматриваемых явлений, называются критериями подобия. Любая комбинация из критериев подобия также представляет собой критерий подобия рассматриваемых физических явлений.

Анализ размерностей – это метод установления связи между физическими величинами, существенными для изучаемого явления, основанный на рассмотрении размерностей этих величин.

Необходимыми условиями физического моделирования являются геометрическое подобие (подобие формы) и физическое подобие модели и натуры: в сходственные моменты времени и в сходственных точках пространства значения переменных величин, характеризующих явления для натуры, должны быть пропорциональны значениям тех же величин для модели.

Одним из видов физического моделирования, применяемым к твёрдым деформируемым телам, является поляризационно-оптический метод исследования напряжений, основанный на , что позволяет исследовать распределение напряжений в различных деталях с помощью их моделей из прозрачных материалов. Поляризационно-оптический метод исследования напряжений – это метод изучения напряжений в деталях машин и строительных конструкциях на прозрачных моделях. Главные значения тензора диэлектрической проницаемости линейно связаны с главными напряжениями.

2. Математическое моделирование
Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта.
Если математическая модель описывается некоторыми уравнениями, то такая модель называется детерминированной.
Если модель описывается некоторыми вероятностными законами, то такая модель называется стохастической.

Основные этапы метода математического моделирования
1. Создание качественной модели.
2. Создание математической модели (постановка математической зада­чи).
а) Выделение существенных факторов.
б) Выделение дополнительных условий (начальных, граничных, условий сопряжения и т.д.).
3. Изучение математической модели.
а) Математическое обоснование модели.
б) Качественное исследование модели. Выяснение поведения модели в крайних и предельных ситуациях.

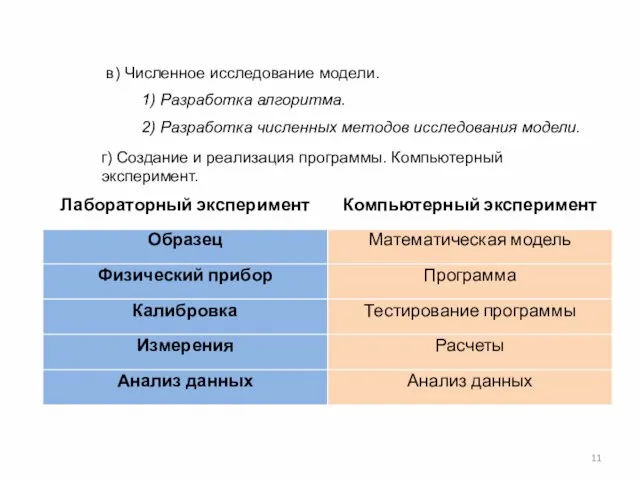
в) Численное исследование модели.
1) Разработка алгоритма.
2) Разработка численных методов исследования модели.
г) Создание и реализация программы. Компьютерный эксперимент.

4. Получение результатов и их интерпретация. Уточнение и модификация модели и методов ее исследования.
5. Использование полученных результатов.

3. Прямые и обратные задачи математического моделирования
1. Прямая задача: все параметры исследуемой системы известны и изучается поведение модели в различных условиях.
2. Обратные задачи:
а) Задача распознавания: определение параметров модели путем сопоставления наблюдаемых данных и результатов моделирования.
б) Задача синтеза (задача математического проектирования): построение математических моделей систем и устройств, которые должны обладать заданными техническими характеристиками.
3. Задача проектирования управляющих систем: особая область математического моделирования, связанная с автоматизированными информационными системами и автоматизированными системами управления.

Универсальность математических моделей. Принцип аналогий
Универсальность математических моделей есть отражение принципа материального единства мира.
Математическая модель должна описывать не только отдельные конкретные явления или объекты, а достаточно широкий круг разнородных явлений и объектов.
Одним из плодотворных подходов к моделированию сложны к объектов является использование аналога и с уже изученными явлениями.
Математическое моделирование для исследования характеристик процесса функционирования систем можно разделить на аналитическое, имитационное и комбинированное.

Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношении алгебраических, интегродифференциальных, конечно-разностных и т. п. или логических условии. Аналитическая модель может быть исследована следующими методами:
а) аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик;
б) численным, когда, не умея решать уравнения в общем виде, стремятся получить числовые результаты при конкретных начальных данных;
в) качественным, когда, не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).

При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования моделируемой системы во времени, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательного протекания во времени, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики исследуемой системы.
Основным преимуществом имитационного моделирования по сравнению с аналитическим является возможность решения более сложных задач.