Строение функции, свойства, графики

Степенные функции.
Ребята, на прошлом уроке мы узнали, как работать с числами с рациональным показателем степени.
На этом уроке мы рассмотрим степенные функции и ограничимся случаем, когда показатель степени рациональный.
Мы будем рассматривать функции вида:
Рассмотрим сначала функции, у которых показатель степени больше одного.

Степенные функции.
Пусть нам дана конкретная функция
Согласно определению, которое мы дали на прошлом уроке x≥0, то есть область определения нашей функции луч [0;+∞).
Давайте, сравним три степенных функции
Число 2,5 лежит между 2 и 3, тогда кажется, что и график нашей функции будет лежать между соответствующими графиками, сравним значения функций при различных х.
1. Если 0
или
2. Если x>1, то но и выполняется
или

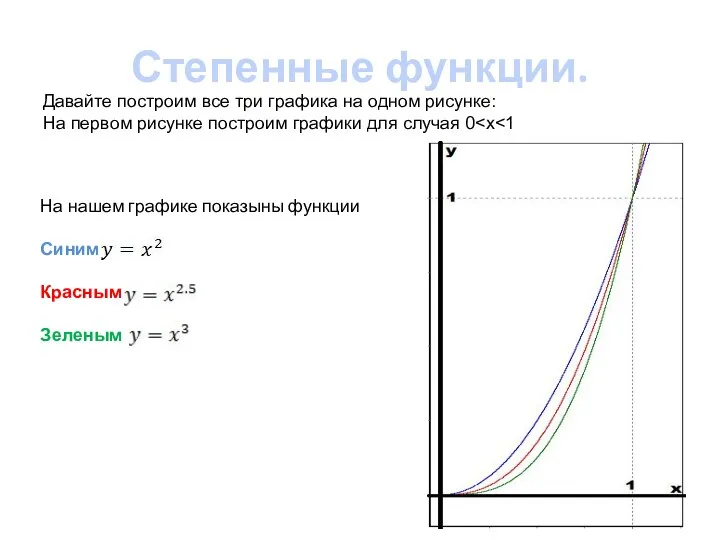
Степенные функции.
Давайте построим все три графика на одном рисунке:
На первом рисунке построим графики для случая 0
На нашем графике показыны функции
Синим
Красным
Зеленым

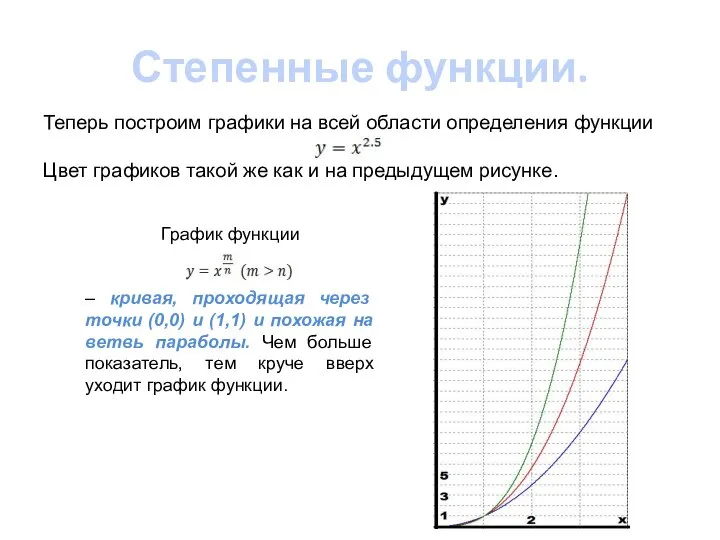
Степенные функции.
Теперь построим графики на всей области определения функции
Цвет графиков такой же как и на предыдущем рисунке.
График функции
– кривая, проходящая через точки (0,0) и (1,1) и похожая на ветвь параболы. Чем больше показатель, тем круче вверх уходит график функции.

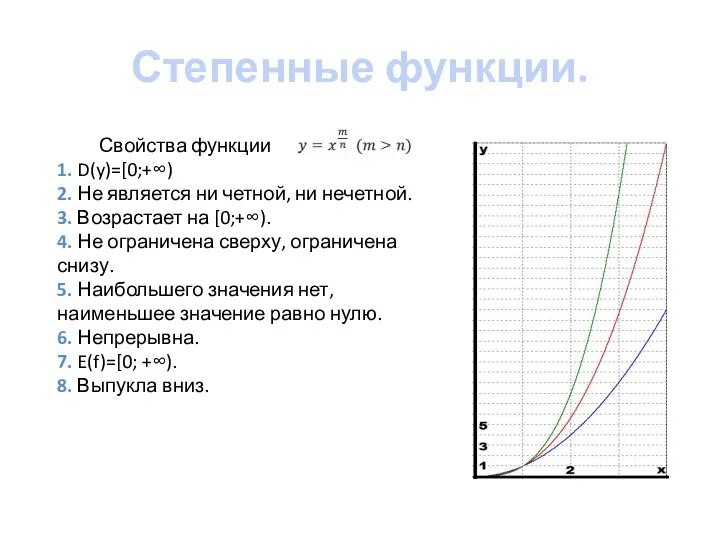
Степенные функции.
Свойства функции
1. D(y)=[0;+∞)
2. Не является ни четной, ни нечетной.
3. Возрастает на [0;+∞).
4. Не ограничена сверху, ограничена снизу.
5. Наибольшего значения нет, наименьшее значение равно нулю.
6. Непрерывна.
7. E(f)=[0; +∞).
8. Выпукла вниз.

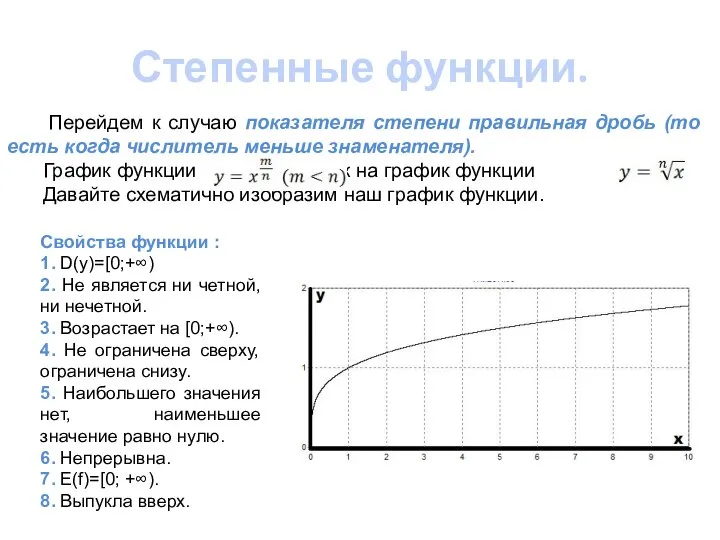
Степенные функции.
Перейдем к случаю показателя степени правильная дробь (то есть когда числитель меньше знаменателя).
График функции похож на график функции
Давайте схематично изобразим наш график функции.
Свойства функции :
1. D(y)=[0;+∞)
2. Не является ни четной, ни нечетной.
3. Возрастает на [0;+∞).
4. Не ограничена сверху, ограничена снизу.
5. Наибольшего значения нет, наименьшее значение равно нулю.
6. Непрерывна.
7. E(f)=[0; +∞).
8. Выпукла вверх.

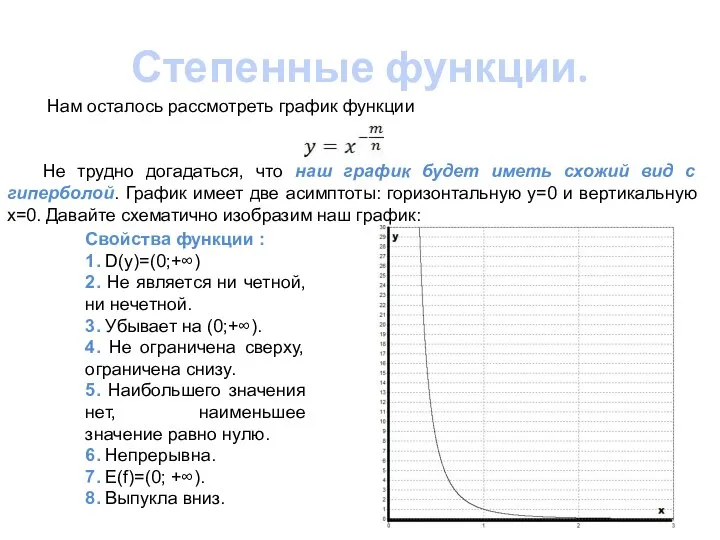
Степенные функции.
Нам осталось рассмотреть график функции
Не трудно догадаться, что наш график будет иметь схожий вид с гиперболой. График имеет две асимптоты: горизонтальную y=0 и вертикальную х=0. Давайте схематично изобразим наш график:
Свойства функции :
1. D(y)=(0;+∞)
2. Не является ни четной, ни нечетной.
3. Убывает на (0;+∞).
4. Не ограничена сверху, ограничена снизу.
5. Наибольшего значения нет, наименьшее значение равно нулю.
6. Непрерывна.
7. E(f)=(0; +∞).
8. Выпукла вниз.

Степенные функции.
Ребята, мы с вами забыли одно очень важное свойство – дифференцируемость функции. Чему равна производная степенной функции с рациональным показателем?
Определение. Если x>0 и r – любое рациональное число, то производная степенной функции
вычисляется по формуле:
Например:

Степенные функции.
Пример.
Найти наибольшее и наименьшее значение функции
на отрезке: а) [1;16] б) (2,10) в) на луче [9;+∞)
Решение.
Показатель степени нашей функции положительный, тогда посмотрев на свойства нашей функции мы видим, что она возрастает на всей области определения, а это значит, что достигает своего наибольшего и наименьшего значения на концах заданных отрезков (если она определена в этих точках)
а)
б) Наибольшего и наименьшего значения функции на этом промежутке нет, так как нам дан открытый промежуток, и точки 0 и 4 этому промежутку не принадлежат.
в)Наибольшьего значения нет.

Степенные функции.
Пример. Найти наибольшее и наименьшее значение функции
на отрезке [1;9].
Решение.
Ребята, вы помните как мы находили наибольшее и наименьшее значение функции на отрезке в 10 классе? Правильно, мы использовали производную, давайте решим наш пример, заодно и повторим алгоритм поиска наименьшего и наибольшего значения.
1. Найдем производную заданной функции:
2. Производная существует на всей области определения исходной функции, тогда критических точек нет.
Найдем стационарные точки:
Заданному отрезку принадлежит только одно решение
Построим таблицу значений нашей функции на концах отрезка и в точке экстремума:
Ответ:

Степенные функции.
Пример. Решить уравнение
Решение.
График функции – возрастает, а график функции у=24-х убывает, ребята мы с вами знаем, если одна функция возрастает, а другая убывает, то они пересекаются только в одной точке, то есть у нас с вами только одно решение.
Заметим:
То есть при х=8 мы получили верное равенство 16=16, это и есть решение нашего уравнения.
Ответ: х=8.

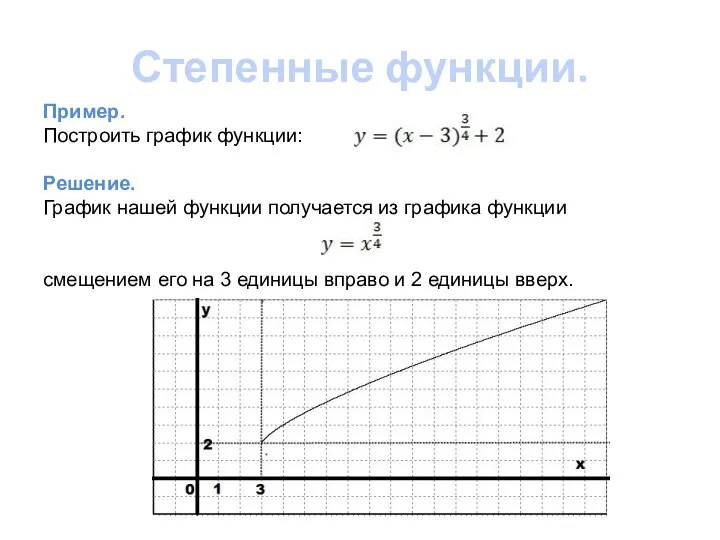
Степенные функции.
Пример.
Построить график функции:
Решение.
График нашей функции получается из графика функции
смещением его на 3 единицы вправо и 2 единицы вверх.

Степенные функции.
Пример. Составить уравнение касательной к прямой
в точке х=1.
Решение. Уравнение касательной определяется известной нам формулой:
В нашем случае a=1.
Найдем производную:
Вычислим:
Найдем уравнение касательной:
Ответ: