Слайд 2Сегодня продолжаем решать логарифмические уравнения

Слайд 3Решить уравнение:
log аf(x) = logа g(x), где а > 0, а ≠

1
Решение этого уравнения основано на следующем важном свойстве: логарифмы двух положительных чисел по одному и тому же основанию равны тогда и только тогда, когда равны эти числа
Слайд 4 Поэтому, чтобы решить это уравнение
а) надо решить f (х) = g(х)
б)

отобрать те корни, которые удовлетворяют условию:
f(х) > 0 и
g(х) > 0
Решить в системе
Слайд 5Пример
Ответ : х = 7. Если число было бы , допустим 1,

оно ответом не было, т.к оно не больше 4 и 2
Слайд 6
Решить уравнения
1. log 3 (3х-1) = log 3(2х+3)
2. log2 (3х -7) =

log2 (2х - 4)
3. log 4(4х - 7) = log4 (х + 2)





 Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции
Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции Математическая статистика
Математическая статистика Угол. Виды углов
Угол. Виды углов Вторая теорема о среднем. Формула Бонне
Вторая теорема о среднем. Формула Бонне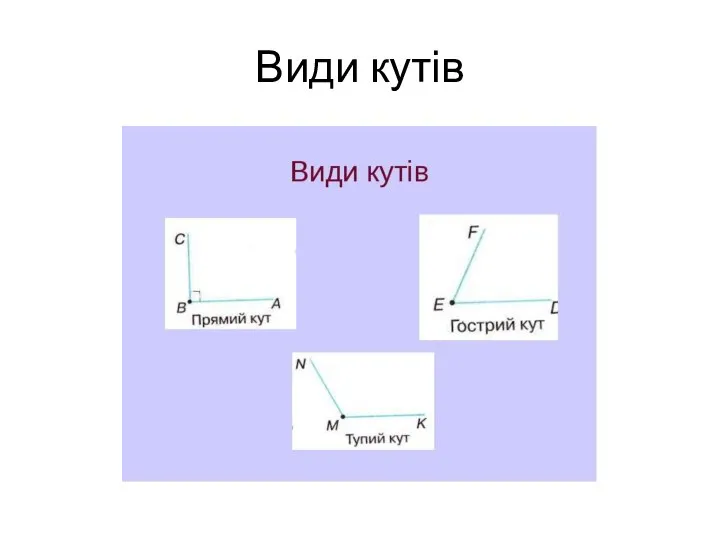 Види кутів
Види кутів Формирование элементарных математических представлений
Формирование элементарных математических представлений Квадратичная функция, ее график. Преобразование графика квадратичной функции
Квадратичная функция, ее график. Преобразование графика квадратичной функции Презентация на тему Использование графов в решении логических задач
Презентация на тему Использование графов в решении логических задач  Работа над ошибками СОР. Подготовка к СОЧ
Работа над ошибками СОР. Подготовка к СОЧ Переместительный закон умножения
Переместительный закон умножения На лесной поляне
На лесной поляне Среднее арифметическое. Задания
Среднее арифметическое. Задания Интеграл и его приложения
Интеграл и его приложения ТАиФЯ № 1 (Введение)
ТАиФЯ № 1 (Введение) Знакомство с деятельностью Ивана Грозного, через решение математических задач
Знакомство с деятельностью Ивана Грозного, через решение математических задач Десятки, единицы, цифры
Десятки, единицы, цифры Числа второго десятка
Числа второго десятка Теорема Пифагора
Теорема Пифагора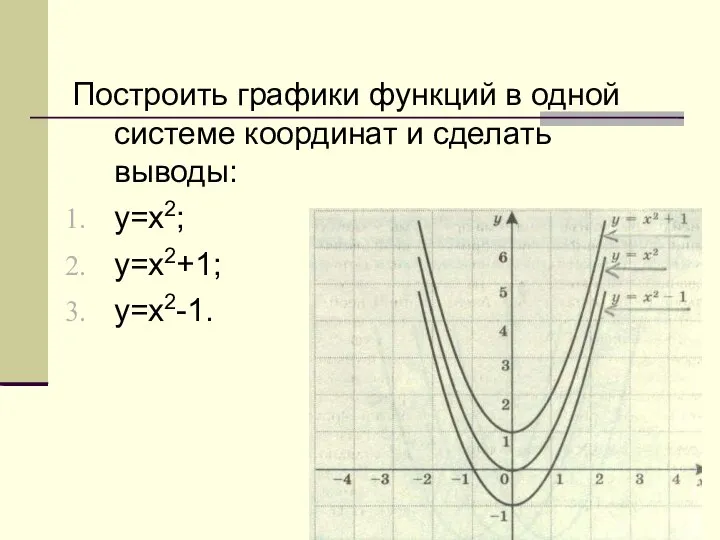 Преобразования графика квадратичной функции. Преобразования графика
Преобразования графика квадратичной функции. Преобразования графика Основные понятия за 100
Основные понятия за 100 Презентация на тему Статистика
Презентация на тему Статистика  Сокращение дробей. 6 класс
Сокращение дробей. 6 класс Презентация на тему Линейная функция и ее график (7 класс)
Презентация на тему Линейная функция и ее график (7 класс)  Математическое моделирование, внедрение методов численного анализа в системах. Расчетный эксперимент
Математическое моделирование, внедрение методов численного анализа в системах. Расчетный эксперимент свойства функции
свойства функции Симметрия относительно прямой
Симметрия относительно прямой Найдите производную функции. Практическая работа
Найдите производную функции. Практическая работа Вычисление логарифмов
Вычисление логарифмов