Слайд 2Возможный вариант классификации
Линейные (прямая)
у=-3х+2
у= ½ х-5
у= -4х
у=-3х+7
у=3х-1
у=-3
у= ½ х
у= -4х+1
у=4х-2
у=3х
у= -4х+5
у=│х+2│
у=│х│
у=│х│-2
у=│х-3│
Квадратичные (парабола)
у=

(х-3)2
у= (х+2)2
у=-х2
у= -½х2
у= -2х2
у=х2-2
Слайд 3Построить график функции
у=-3х+2
у= -½х2

Слайд 4Возможный вариант классификации
Могу построить
у=-3х+2
у=│х│
у= (х-3)2
у= ½ х-5
у= -4х
у= х2+1
у=-3х+7
у=-х2
у=3х-1
у=-3
Не могу построить
у=│х+2│
у=

(х-3)2
у= (х+2)2
у=х2-2
у=│х│-2
у=│х-3│
у=-3
у= -½х2
у= ½ х
у= -4х+1
у= -2х2
у=4х-2
у=х2-3
у=3х
у=-3х+2
Слайд 5Алгоритм построения графика по точкам:
Составить таблицу с шагом 1 (чем мельче шаг

– тем точнее график; чем больше точек – тем точнее график)
Отметить точки на координатной плоскости.
Соединить точки линией (какой – внимание!)
Слайд 6Групповая работа. (5минут)
у=│х-3│,где -4≤ х ≤4
у=│х│ -2 ,где -4≤ х ≤4
у=х2-2 ,где

-4≤ х ≤4
у= (х+2)2 ,где -4≤ х ≤4
у= (х-3)2 ,где -4≤ х ≤4
у=│х+2│ ,где -4≤ х ≤4
Слайд 7Групповая работа. (5минут)
у=│х-3│
у=│х│ -2
у=х2-2
у= (х+2)2
у= (х-3)2
у=│х+2│

Слайд 8Алгоритм построения графика с помощью движений.
Построить график функции у=f(x)
у=f(x)+а – вверх

на а
у=f(x)-а – вниз на а
у=f(x-а) – вправо на а
у=f(x+а) – влево на а
Слайд 9Построение графика с помощью движений.
Удалось ли увидеть закономерность и совершить открытие? (если

не получилось, то почему)
Как работала группа? (слаженно или нет, были ли конфликты, кто в группе самый ценный игрок)
Сможете ли применить свои знания на практике? (если нет, то почему)
Какую оценку можно поставить группе за работу?
Оцените работу каждого игрока, поставьте отметку.








 Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях
Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях Методы и приемы решения дробно-рациональных уравнений, содержащих параметр
Методы и приемы решения дробно-рациональных уравнений, содержащих параметр Декартова система координат на плоскости. Математика, 6 класс
Декартова система координат на плоскости. Математика, 6 класс Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Цифровая азбука
Цифровая азбука Теоремы синусов и косинусов
Теоремы синусов и косинусов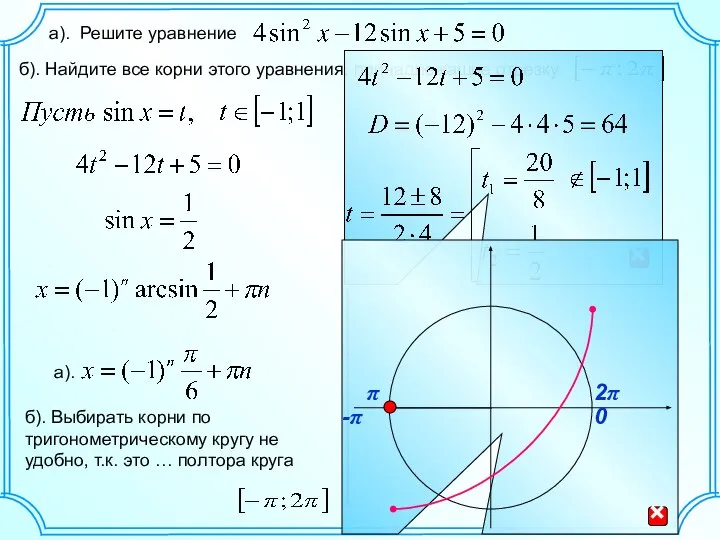 Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Закон Ома. Решение задач
Закон Ома. Решение задач Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел
Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел Площадь полной поверхности призмы
Площадь полной поверхности призмы Комбинаторные задачи
Комбинаторные задачи Радианная мера угла
Радианная мера угла Основные тригонометрические тождества. Формулы приведения
Основные тригонометрические тождества. Формулы приведения Vorlesung. Blatt 2
Vorlesung. Blatt 2 Соста числа 11
Соста числа 11 Тригонометрические уравнения
Тригонометрические уравнения Презентация на тему Стандартный вид числа 9 класс
Презентация на тему Стандартный вид числа 9 класс  Лекция 0
Лекция 0 Элементы математической статистики, комбинаторики и теории вероятностей
Элементы математической статистики, комбинаторики и теории вероятностей Презентация на тему Плоскость. Прямая. Луч
Презентация на тему Плоскость. Прямая. Луч  Симметрия. 9 класс
Симметрия. 9 класс Алгоритм Евклида
Алгоритм Евклида Второй и третий признаки равенства треугольников
Второй и третий признаки равенства треугольников Призмы. Виды призм
Призмы. Виды призм Приключения Буратино в Стране Финансов
Приключения Буратино в Стране Финансов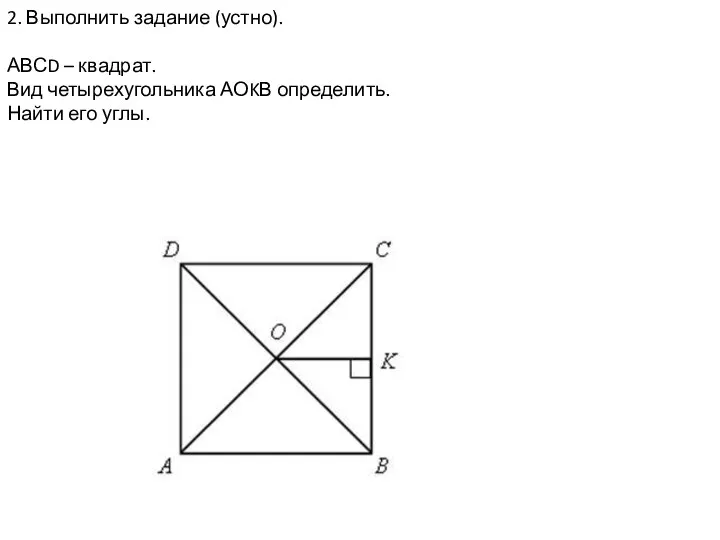 Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Периметр и площадь
Периметр и площадь Матрицы и определители
Матрицы и определители