Содержание
- 2. I. Примеры Найти общий интеграл. Поделим обе части на чтобы разделить переменные. Проинтегрируем обе части: -
- 3. Перепишем уравнение, заменив на - общий интеграл 2.
- 4. - общий интеграл Приведем уравнение к уравнению с разделяющимися переменными, вынося общие множители за скобки: 3.
- 5. 4. Найти частный интеграл уравнения удовлетворяющий начальному условию Найдем вначале общий интеграл.
- 6. - общее решение Используя начальное условие, подставляем в общее решение значения Найденное значение константы подставляем в
- 7. Дифференциальное уравнение называется линейным, если оно линейно (т.е. первой степени) относительно искомой функции и её производной
- 8. Интегрируем: здесь Пример. Найти общее решение. Здесь и тогда - искомое общее решение
- 9. III. Дифференциальные уравнения высших порядков, допускающие понижение порядка. Уравнение вида решается последовательным n-кратным интегрированием. Умножаем обе
- 10. Пример.
- 11. которое получается из уравнения (1) заменой в нём производных искомой функции соответствующими степенями , причём сама
- 12. где и - линейно независимые частные решения уравнения (1), а и - произвольные постоянные. Общее решение
- 13. Общее решение имеет вид: Примеры выделения чисел и : 1. 2.
- 14. Примеры интегрирования уравнений 1. Характеристическое уравнение: Имеем случай 1) - общее решение 2. Характеристическое уравнение: Имеем
- 15. 3. Характеристическое уравнение: Имеем случай 3). Общее решение: 4. Найти частное решение уравнения с начальными условиями
- 17. Скачать презентацию














 Геометрия в жизни человека
Геометрия в жизни человека Действия с десятичными дробями
Действия с десятичными дробями Оператор Лапласа в полярных, цилиндрических и сферических системах координат
Оператор Лапласа в полярных, цилиндрических и сферических системах координат Решение задач. Линейные динамические системы
Решение задач. Линейные динамические системы Логарифмические уравнения
Логарифмические уравнения Статистическое наблюдение
Статистическое наблюдение Презентация на тему Параллелепипед и его объем
Презентация на тему Параллелепипед и его объем  Презентация на тему ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
Презентация на тему ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ  Презентация на тему Задачи по теме треугольники
Презентация на тему Задачи по теме треугольники  Баскетбол. Математическая викторина
Баскетбол. Математическая викторина Первое знакомство с понятием вероятность. Урок 145
Первое знакомство с понятием вероятность. Урок 145 Измерительные работы
Измерительные работы Правильные многогранники
Правильные многогранники Рассчитать площадь и периметр прямоугольника по двум известным сторонам. Алгоритм решения подобных задач
Рассчитать площадь и периметр прямоугольника по двум известным сторонам. Алгоритм решения подобных задач Шаг в науку. Мир фракталов
Шаг в науку. Мир фракталов Презентация на тему Логарифмическая функция в уравнениях
Презентация на тему Логарифмическая функция в уравнениях  Презентация на тему Параллельность прямых и плоскостей (10 класс)
Презентация на тему Параллельность прямых и плоскостей (10 класс)  Основы тригонометрии. Упражнения
Основы тригонометрии. Упражнения Геометрия Евклида
Геометрия Евклида Дроби, проценты, пропорции в задачах с экономическим содержанием
Дроби, проценты, пропорции в задачах с экономическим содержанием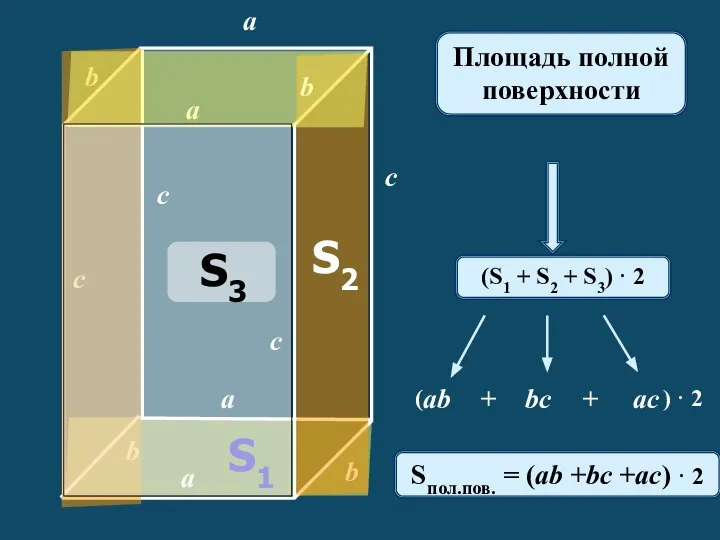 Площадь полной поверхности
Площадь полной поверхности Статистмческие методы
Статистмческие методы Решение линейных уравнений. Часть 2
Решение линейных уравнений. Часть 2 формулы нахождения периметра прямоугольника, периметра квадрата
формулы нахождения периметра прямоугольника, периметра квадрата Презентация на тему Таблицы истинности
Презентация на тему Таблицы истинности  Формула Ньютона-Лейбница. Площадь криволинейной трапеции
Формула Ньютона-Лейбница. Площадь криволинейной трапеции Радианная мера угла. Синус, косинус, тангенс числа
Радианная мера угла. Синус, косинус, тангенс числа Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ