- Главная
- Математика
- Логарифмы

Содержание
- 2. История создания Предпосылки к открытию логарифмов были уже в Античности. Архимед знал о связи между арифметической
- 3. Джон Непер-отец логарифмов В начале XVI века два ученых, не зная об исследованиях друг друга, опубликовали
- 4. Дальнейшая история логарифмов В 1620 году Эдмунд Уингейт предложил модель логарифмической линейки. И до изобретения калькулятора
- 6. Другие области применения логарифмов 1)интенсивность звука (децибелы) в физике; 2)шкала яркости звёзд в астрономии; 3)активность водородных
- 7. Спасибо за внимание!
- 9. Скачать презентацию
Слайд 2История создания
Предпосылки к открытию логарифмов были уже в Античности. Архимед знал о связи между арифметической
История создания
Предпосылки к открытию логарифмов были уже в Античности. Архимед знал о связи между арифметической

и геометрической прогрессиями, а также о некоторых свойствах степеней с натуральным показателем.
Большой толчок к развитию не только математики, но и других естественных наук дала Эпоха Великих Географических Открытий. Население росло, запасы истощались, и в поисках новых земель и приключений отважные мореплаватели отправлялись бороздить просторы всех шести океанов. И, чтобы точно проложить курс через моря и океаны, сложить 5 и 7 было явно недостаточно.
Нужны были сложные расчеты с привязкой к звездному небу, учитывающие расположение звезд и конфигурацию планет, для определения курса корабля, а калькулятор в карманы лосин, туго обтягивающих бедра капитана корабля, не помещался. Астрономы тратили несколько месяцев на трудоемкие расчеты с многозначными числами. В середине XV столетия, сопоставляя значения геометрических и арифметических прогрессий, кому-то из светлых умов пришла идея в расчетах заменить умножение многозначных чисел с громоздкими результатами сложением, взяв геометрическую прогрессию за исходную.
Впервые примеры таких расчетов в 1544 году в книге «Arithmetica integra» опубликовал Михаэль Штифель. Революционной идей ученого был переход от целых показателей степеней к произвольным рациональным числам. Однако развивать свою идею дальше и составлять таблицы для вычислений он не стал.
Большой толчок к развитию не только математики, но и других естественных наук дала Эпоха Великих Географических Открытий. Население росло, запасы истощались, и в поисках новых земель и приключений отважные мореплаватели отправлялись бороздить просторы всех шести океанов. И, чтобы точно проложить курс через моря и океаны, сложить 5 и 7 было явно недостаточно.
Нужны были сложные расчеты с привязкой к звездному небу, учитывающие расположение звезд и конфигурацию планет, для определения курса корабля, а калькулятор в карманы лосин, туго обтягивающих бедра капитана корабля, не помещался. Астрономы тратили несколько месяцев на трудоемкие расчеты с многозначными числами. В середине XV столетия, сопоставляя значения геометрических и арифметических прогрессий, кому-то из светлых умов пришла идея в расчетах заменить умножение многозначных чисел с громоздкими результатами сложением, взяв геометрическую прогрессию за исходную.
Впервые примеры таких расчетов в 1544 году в книге «Arithmetica integra» опубликовал Михаэль Штифель. Революционной идей ученого был переход от целых показателей степеней к произвольным рациональным числам. Однако развивать свою идею дальше и составлять таблицы для вычислений он не стал.
Слайд 3
Джон Непер-отец логарифмов
В начале XVI века два ученых, не зная об исследованиях друг друга, опубликовали
Джон Непер-отец логарифмов
В начале XVI века два ученых, не зная об исследованиях друг друга, опубликовали

свои работы по изучению арифметических и геометрических прогрессий: В 1614 г. шотландский математик Джон Непер опубликовал книгу «Описание удивительной таблицы логарифмов».
В 1620 г. из-под пера швейцарского ученого Иоста Бюрги вышел труд «Таблицы арифметической и геометрической прогрессий, вместе с основательным наставлением, как их нужно понимать и с пользой применять во всяческих вычислениях. Бюрги украл идею Непера. Но во времена, когда не было интернета и международных научных симпозиумов, а информация распространялась «голубиной почтой», 6 лет — не такой большой срок. А одновременное открытие логарифмов, в странах разделенных не только расстоянием, но и языковым барьером, как раз свидетельствует о важности этого открытия. Учитывая, что Джон Непер предложил придуманный им способ вычислений называть логарифм (от греческих слов logos – «отношение» и arithmos – «число», а вместе – «число отношений»), он по праву считается отцом логарифмов.
Еще шотландский математик составил специальные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1 и с точностью до восьми знаков. С началом практического использования таблиц Непера умножение многозначных чисел и извлечение корней значительно упростилось.
В 1620 г. из-под пера швейцарского ученого Иоста Бюрги вышел труд «Таблицы арифметической и геометрической прогрессий, вместе с основательным наставлением, как их нужно понимать и с пользой применять во всяческих вычислениях. Бюрги украл идею Непера. Но во времена, когда не было интернета и международных научных симпозиумов, а информация распространялась «голубиной почтой», 6 лет — не такой большой срок. А одновременное открытие логарифмов, в странах разделенных не только расстоянием, но и языковым барьером, как раз свидетельствует о важности этого открытия. Учитывая, что Джон Непер предложил придуманный им способ вычислений называть логарифм (от греческих слов logos – «отношение» и arithmos – «число», а вместе – «число отношений»), он по праву считается отцом логарифмов.
Еще шотландский математик составил специальные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1 и с точностью до восьми знаков. С началом практического использования таблиц Непера умножение многозначных чисел и извлечение корней значительно упростилось.
Слайд 4
Дальнейшая история логарифмов
В 1620 году Эдмунд Уингейт предложил модель логарифмической линейки. И до изобретения калькулятора логарифмическая
Дальнейшая история логарифмов
В 1620 году Эдмунд Уингейт предложил модель логарифмической линейки. И до изобретения калькулятора логарифмическая

линейка оставалась незаменимым помощником инженеров, мореплавателей, и других ученых, которым требовалась работа с большими числами. Впоследствии многие ученые создавали свои таблицы логарифмов, уточняя их значения. Не обошел своим вниманием эту тему и Иоган Кеплер — известный ученый не только открыл законы движения небесных тел, но и составил астрономические таблицы, которые опубликовал в 1624 году с восторженным посвящением Джону Неперу, не зная о смерти отца логарифмов.
Наиболее близко к современному определению логарифмирования подошли Валлис (1685) и Иоганн Бернулли (1694). Эйлер окончательно узаконил логарифмирование как математическое действие, обратное возведению в степень. Многие ученые в своих вычислениях стали пользоваться таблицами логарифмов, а Лаплас Пьер Симон в одном из своих трудов написал фразу, вынесенную в эпиграф статьи: «Изобретение логарифмов, сократив вычисления нескольких месяцев в труд нескольких дней, словно удваивает жизнь астрономов». Астрономами в то время называли не только любителей звездного неба, каждый вечер настраивающих свои телескопы в поисках новых и сверхновых звезд, а любого ученого, использующего в своих расчетах сложные вычисления.
Наиболее близко к современному определению логарифмирования подошли Валлис (1685) и Иоганн Бернулли (1694). Эйлер окончательно узаконил логарифмирование как математическое действие, обратное возведению в степень. Многие ученые в своих вычислениях стали пользоваться таблицами логарифмов, а Лаплас Пьер Симон в одном из своих трудов написал фразу, вынесенную в эпиграф статьи: «Изобретение логарифмов, сократив вычисления нескольких месяцев в труд нескольких дней, словно удваивает жизнь астрономов». Астрономами в то время называли не только любителей звездного неба, каждый вечер настраивающих свои телескопы в поисках новых и сверхновых звезд, а любого ученого, использующего в своих расчетах сложные вычисления.
Слайд 6
Другие области применения логарифмов
1)интенсивность звука (децибелы) в физике;
2)шкала яркости звёзд в астрономии;
3)активность
Другие области применения логарифмов
1)интенсивность звука (децибелы) в физике;
2)шкала яркости звёзд в астрономии;
3)активность

водородных ионов (pH) в химии;
4)шкала Рихтера для определения интенсивности землетрясения в сейсмологии;
5)логарифмическая шкала времени в истории.
4)шкала Рихтера для определения интенсивности землетрясения в сейсмологии;
5)логарифмическая шкала времени в истории.
Слайд 7Спасибо за внимание!
Спасибо за внимание!

- Предыдущая
Структура проблемного портфеляСледующая -
Профилактика утомления
 Сколько? Как? Почему? Математическая игра
Сколько? Как? Почему? Математическая игра Десятичные дроби. Тест
Десятичные дроби. Тест Презентация по математике "Свойства величин" -
Презентация по математике "Свойства величин" -  Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Уравнение сферы
Уравнение сферы Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе
Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе Бинарные отношения
Бинарные отношения Неисключенные остатки систематической погрешности. Статистическая обработка однократных наблюдений. Случайные погрешности
Неисключенные остатки систематической погрешности. Статистическая обработка однократных наблюдений. Случайные погрешности Учимся писать цифры
Учимся писать цифры Задача о железнодорожных составах
Задача о железнодорожных составах Доказательство неравенств
Доказательство неравенств Исследование лингвистических модификаторов нечётких множеств в среде MathСad
Исследование лингвистических модификаторов нечётких множеств в среде MathСad Дискретная математика. Лекция 1. Введение
Дискретная математика. Лекция 1. Введение Построение треугольника. 5 класс
Построение треугольника. 5 класс Центральная и осевая симметрия
Центральная и осевая симметрия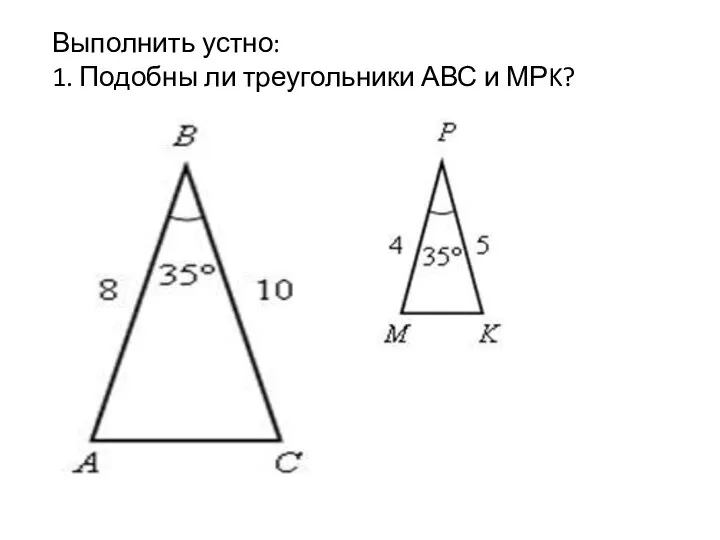 Признаки подобия треугольников. Урок 34
Признаки подобия треугольников. Урок 34 Презентация на тему Тригонометрические функции
Презентация на тему Тригонометрические функции  Основное свойство арифметического квадратного корня
Основное свойство арифметического квадратного корня Корреляция. Показатель корреляции
Корреляция. Показатель корреляции Корни. Арифметический корень
Корни. Арифметический корень Окружность. Свойство отрезков, хорд, секущих и касательных
Окружность. Свойство отрезков, хорд, секущих и касательных Кратные числа
Кратные числа Приближенные вычисления
Приближенные вычисления Скалярное произведение векторов
Скалярное произведение векторов Решение задача на совместную работу. 6 класс
Решение задача на совместную работу. 6 класс Математические действия в разных системах исчисления
Математические действия в разных системах исчисления Объемы многогранников и тел вращения. Устная работа
Объемы многогранников и тел вращения. Устная работа Четные и нечетные числа
Четные и нечетные числа