Содержание
- 2. Определение: Функция F(х) называется первообразной функции f(х) на промежутке Х, если Теорема: Если функция f(х) непрерывна
- 3. Пример: Решение. Данная функция может быть записана в виде:
- 4. Замечание 2: Если функция f(х) определена на промежутке Х и в точке имеет разрыв в виде
- 5. Основные свойства неопределенного интеграла.
- 6. Основные методы Интегрирования.
- 7. Табличный. Сведение к табличному преобразованием подынтегрального выражения в сумму или разность. Интегрирование с помощью замены переменной
- 8. Нахождение интеграла методом преобразования подынтегральной функции в сумму или разность.
- 9. Интегрирование методом замены переменной.
- 11. Интегрирование выражений, содержащих радикалы, методом подстановки.
- 13. Интегрирование алгебраических дробей.
- 14. Интегрирование по частям.
- 17. Скачать презентацию








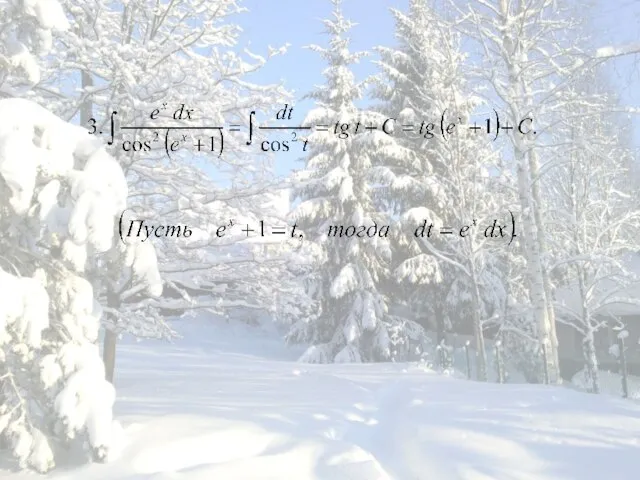





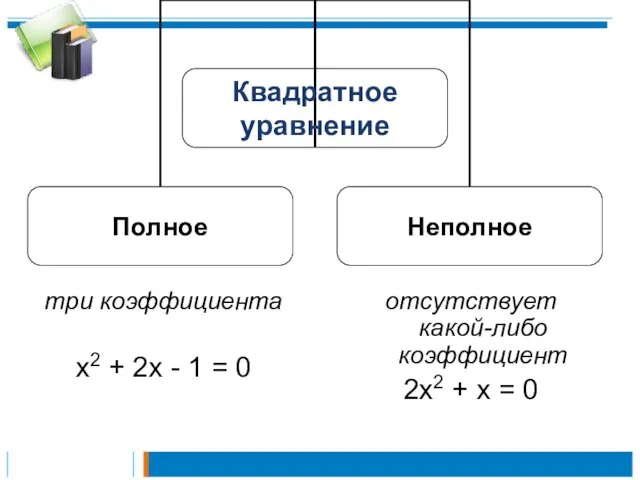 Неполные квадратные уравнения
Неполные квадратные уравнения Умножение одночленов. Возведение одночлена в степень
Умножение одночленов. Возведение одночлена в степень Математика ЕГЭ. Треугольники
Математика ЕГЭ. Треугольники Геометрия. Повторение
Геометрия. Повторение Векторная алгебра. Основные определения
Векторная алгебра. Основные определения Вычисление площадей плоских фигур. Трапеция
Вычисление площадей плоских фигур. Трапеция Математический диктант
Математический диктант Контрольная работа
Контрольная работа Граф. Построение графов
Граф. Построение графов Мир логарифмов. 11 класс
Мир логарифмов. 11 класс Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Домашняя работа по математике
Домашняя работа по математике Цветочное настроение. Математика
Цветочное настроение. Математика Решение систем линейных неравенств с одной переменной (9 класс)
Решение систем линейных неравенств с одной переменной (9 класс) Надежность технических систем
Надежность технических систем Работа с числами
Работа с числами Функции одной и нескольких переменных
Функции одной и нескольких переменных Презентация на тему Преобразование графиков функций на координатной плоскости
Презентация на тему Преобразование графиков функций на координатной плоскости  Знакомство с линейкой
Знакомство с линейкой Ось симметрии фигуры
Ось симметрии фигуры Числовые великаны вокруг и внутри нас
Числовые великаны вокруг и внутри нас Числовая окружность в координатной плоскости
Числовая окружность в координатной плоскости Статистика. Введение в теорию вероятности. Основные понятия
Статистика. Введение в теорию вероятности. Основные понятия Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис
Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис Сфера и шар
Сфера и шар История появления тригонометрии
История появления тригонометрии Функция y = x2 и её график
Функция y = x2 и её график Действия с числами, записанными в стандартном виде
Действия с числами, записанными в стандартном виде