Содержание
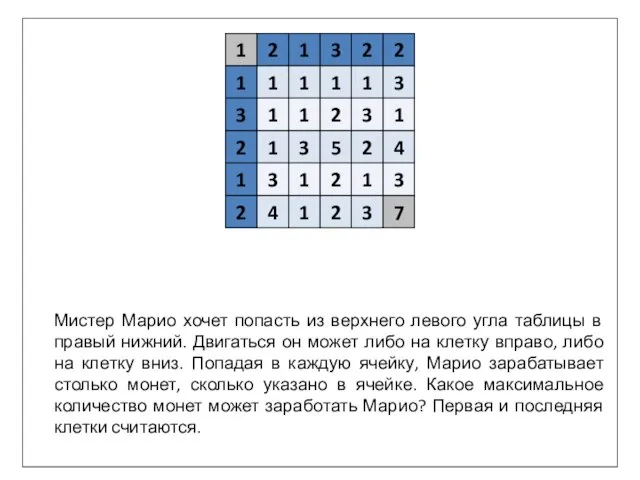
- 2. Мистер Марио хочет попасть из верхнего левого угла таблицы в правый нижний. Двигаться он может либо
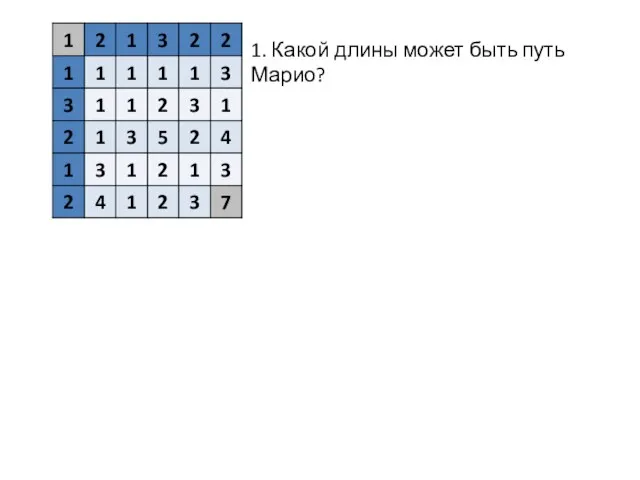
- 3. 1. Какой длины может быть путь Марио?
- 4. 1. Какой длины может быть путь Марио? Оказывается длина пути не зависит от пути и всегда
- 5. 1. Какой длины может быть путь Марио? Оказывается длина пути не зависит от пути и всегда
- 6. 1. Какой длины может быть путь Марио? Оказывается длина пути не зависит от пути и всегда
- 7. 1. Какой длины может быть путь Марио? Оказывается длина пути не зависит от пути и всегда
- 8. 1. Какой длины может быть путь Марио? Оказывается длина пути не зависит от пути и всегда
- 9. 1. Какой длины может быть путь Марио? Оказывается длина пути не зависит от пути и всегда
- 10. 1. Какой длины может быть путь Марио? Оказывается длина пути не зависит от пути и всегда
- 11. 1. Какой длины может быть путь Марио? Оказывается длина пути не зависит от пути и всегда
- 12. 1. Какой длины может быть путь Марио? Оказывается длина пути не зависит от пути и всегда
- 13. 1. Какой длины может быть путь Марио? Оказывается длина пути не зависит от пути и всегда
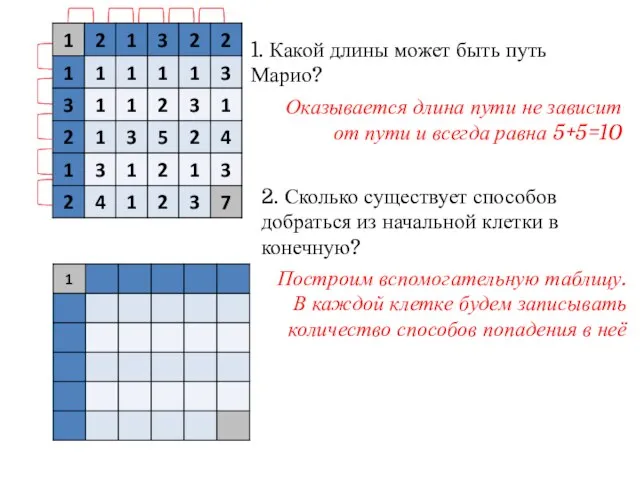
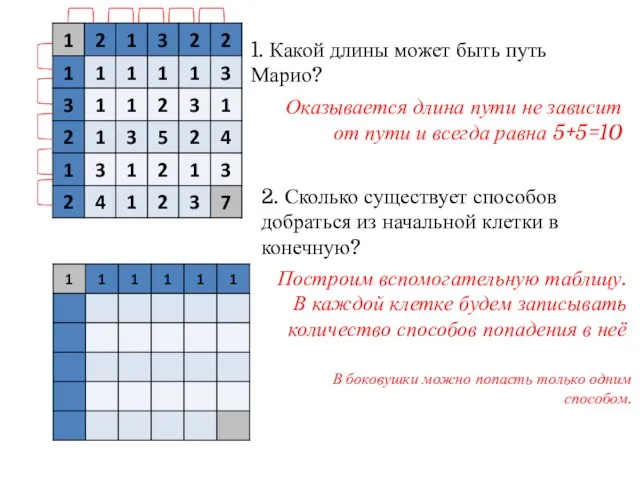
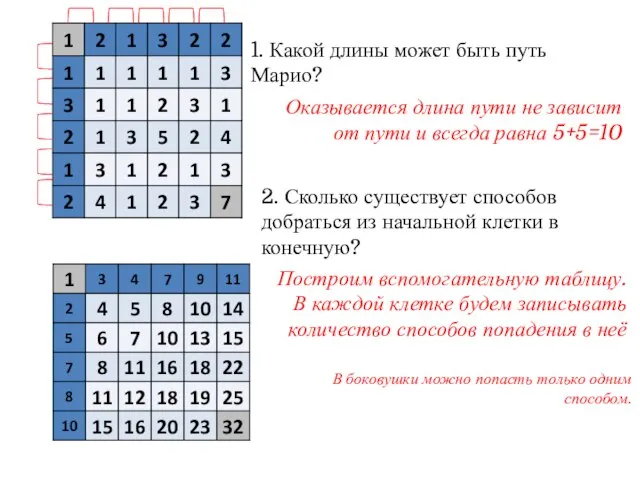
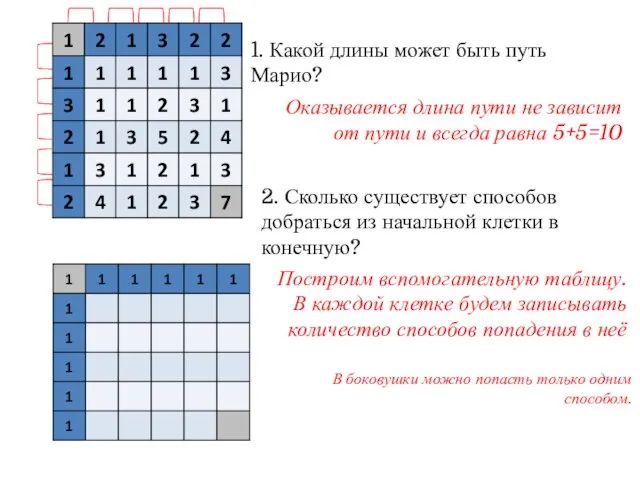
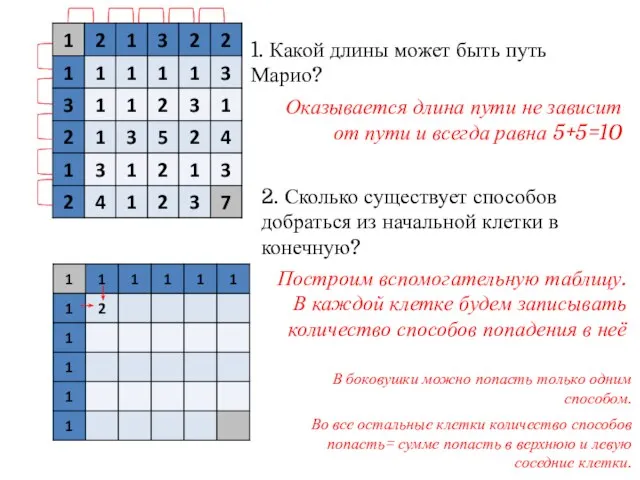
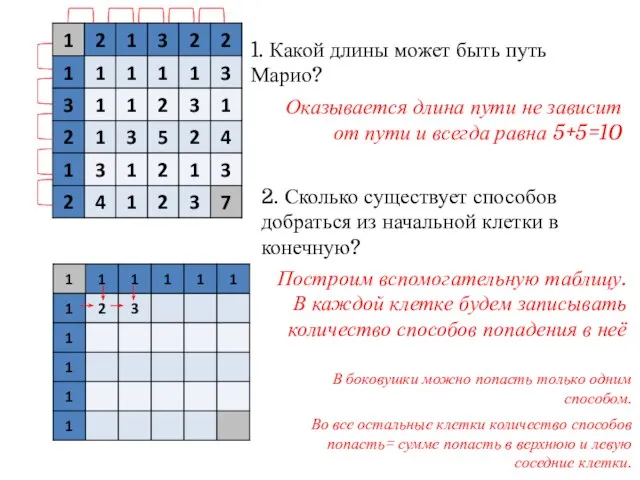
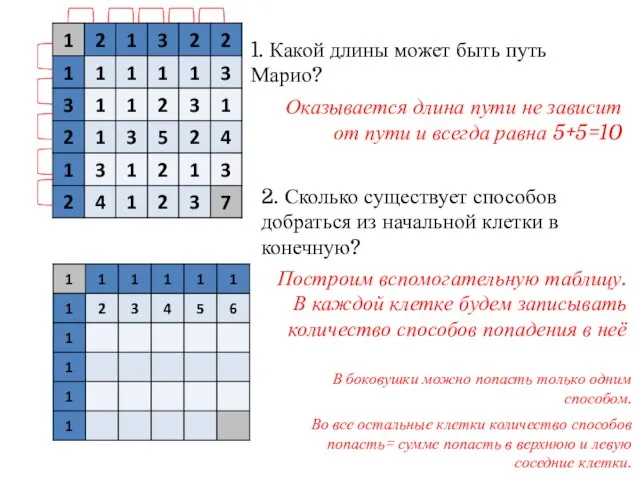
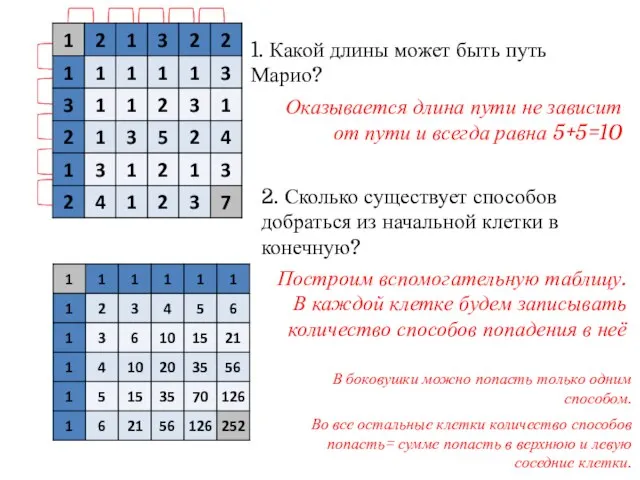
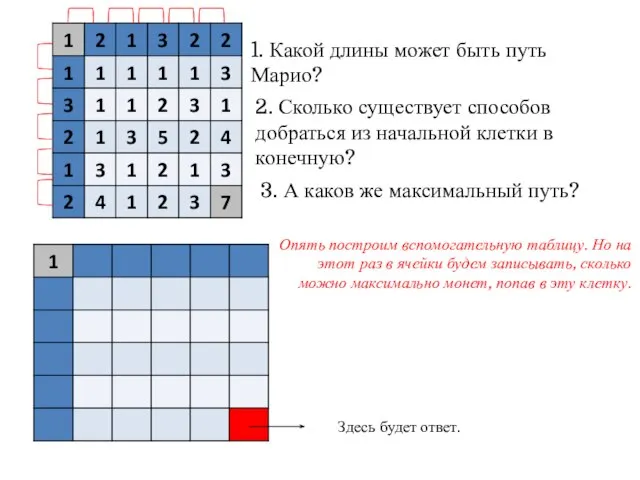
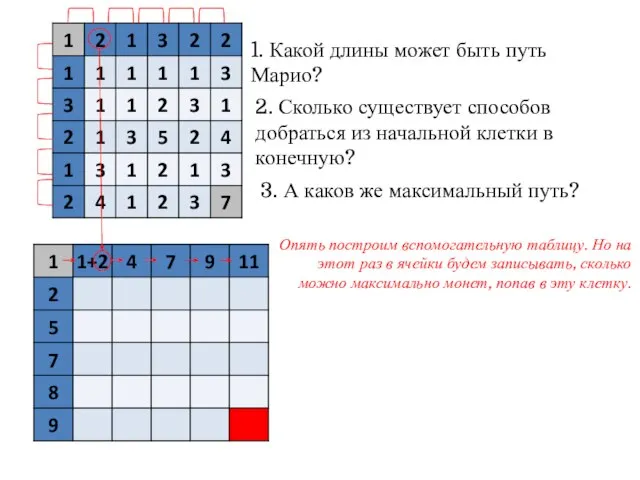
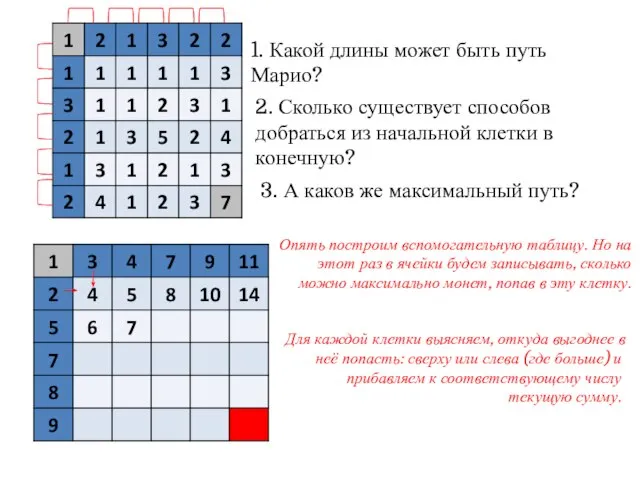
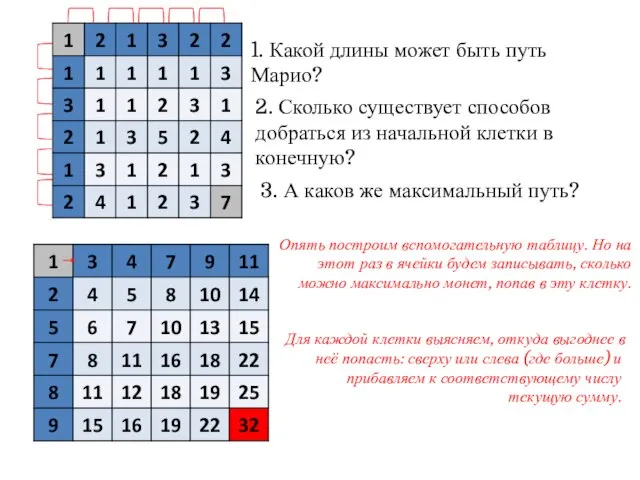
- 14. 1. Какой длины может быть путь Марио? 2. Сколько существует способов добраться из начальной клетки в
- 15. 1. Какой длины может быть путь Марио? 2. Сколько существует способов добраться из начальной клетки в
- 16. 1. Какой длины может быть путь Марио? 2. Сколько существует способов добраться из начальной клетки в
- 17. 1. Какой длины может быть путь Марио? 2. Сколько существует способов добраться из начальной клетки в
- 19. Скачать презентацию


 Симметрия в природе
Симметрия в природе Решение задач. Урок 22
Решение задач. Урок 22 Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ  Тест. Округление чисел до десятков, сотен
Тест. Округление чисел до десятков, сотен Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Умножение и деление дробей
Умножение и деление дробей Математика в лицах
Математика в лицах Решение задач на проценты. Концентрация
Решение задач на проценты. Концентрация Проценты. Проценты в древности
Проценты. Проценты в древности Многоэтажные дроби. 8 класс
Многоэтажные дроби. 8 класс Подготовка к контрольной работе
Подготовка к контрольной работе Естественно балансирующееся общество
Естественно балансирующееся общество Способы решения задач на смеси и сплавы
Способы решения задач на смеси и сплавы Дидактические материалы на уроках математики
Дидактические материалы на уроках математики Действия с величинами. Урок №4
Действия с величинами. Урок №4 Аксиомы стереометрии
Аксиомы стереометрии Практикум по решению задач
Практикум по решению задач Числовые функции
Числовые функции Сокращение дробей
Сокращение дробей Устное решение задач по готовым чертежам
Устное решение задач по готовым чертежам Аксиомы стереометрии
Аксиомы стереометрии Математическая викторина
Математическая викторина Решение показательных уравнений. 10 класс. Учебник С. М. Никольского
Решение показательных уравнений. 10 класс. Учебник С. М. Никольского Математическая статистика. Формула классической вероятности
Математическая статистика. Формула классической вероятности Площадь многоугольника
Площадь многоугольника Исследование функций и построение графиков
Исследование функций и построение графиков Основы теории вероятностей или случайные события ( лекция 2)
Основы теории вероятностей или случайные события ( лекция 2) Дисперсионный анализ
Дисперсионный анализ