Содержание
- 2. Основные положения Наука — сфера человеческой деятельности, направленной на выработку и систематизацию достоверных знаний о действительности
- 3. Основные положения Как получить достоверные знания? - пассивно-созерцательная теория Дидро [2] (главное это ощущения); идеализм Гегеля
- 4. Основные положения Настоящая революция в методологии научных исследований произошла лишь тогда, когда роль критерия истинности знания
- 5. Эксперимент Эксперимент может проводиться с целью: — определить, какие величины и насколько влияют на исследуемый объект
- 6. Эксперимент Теория эксперимента — наука, занимающаяся вопросами правильной организации экспериментальных исследований — включает три основных направления:
- 7. Эксперимент Исследование машины или процесса начинается с разработки физической модели, а затем, на ее основании, строится
- 8. Эксперимент Математическая модель процесса представляет собой аналитическое описание связей между отдельными элементами физической модели. В положении
- 9. Эксперимент
- 10. Эксперимент
- 11. Эксперимент
- 12. Практическое занятие №1 ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНОЙ ОТНОСИТЕЛЬНОЙ ОШИБКИ ФУНКЦИИ Для выполнения работы используются: 1. Измерительная линейка с
- 13. Практическое занятие №1 маятник №1 Примем длину нити маятника около 500 мм. Отклонив маятник на угол
- 14. Практическое занятие №1 маятник №1 Таблица 1 Результаты 50 измерений
- 15. Практическое занятие №1 маятник №2 Уменьшите длину маятника до 450 мм. Провести измерения один раз. Таблица
- 16. Практическое занятие №1 маятник №3 Уменьшите длину маятника до 400 мм. Провести измерения пять раз. Таблица
- 17. Практическое занятие №1 маятник №4 Уменьшите длину маятника до 350 мм. Провести измерения пятнадцать раз. Таблица
- 18. Погрешности результатов измерений
- 19. Погрешности результатов измерений
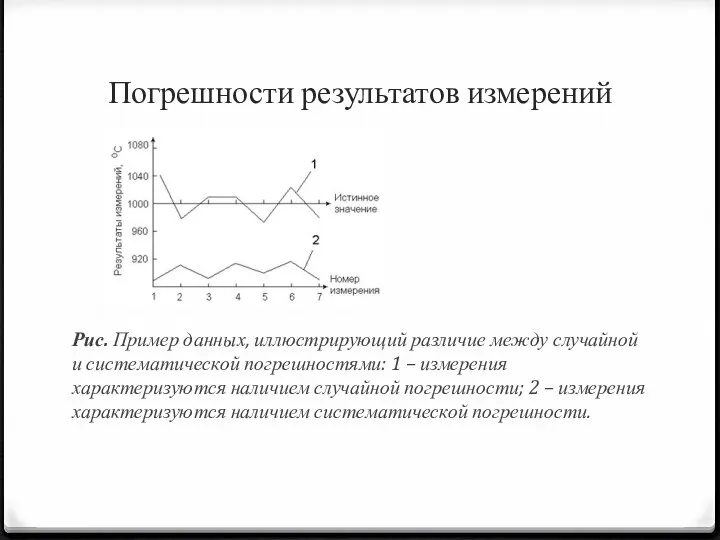
- 20. Погрешности результатов измерений Систематической называется погрешность, которая при повторных экспериментах остается постоянной или изменяется закономерно. Наличие
- 21. Погрешности результатов измерений Случайной называется погрешность, обусловленная действием ряда причин, меняющихся случайным образом от эксперимента к
- 22. Погрешности результатов измерений Рис. Пример данных, иллюстрирующий различие между случайной и систематической погрешностями: 1 – измерения
- 23. Погрешности результатов измерений инструментальные (приборные или аппаратурные) погрешности средств измерений называются такие, которые принадлежат данному средству
- 24. Погрешности результатов измерений методические погрешности – это погрешности, которые не могут быть приписаны данному прибору, не
- 25. Погрешности результатов измерений субъективные погрешности, обусловленные особенностями исследователя. Следует иметь ввиду, что полностью исключить систематические погрешности
- 26. Законы распределения вероятностей случайных величин Случайные величины бывают дискретными и непрерывными. Дискретные величины способны принимать лишь
- 27. Законы распределения вероятностей случайных величин Исследователь при постановке опытов делает конечное, обычно небольшое, количество измерений. Их
- 28. Законы распределения вероятностей случайных величин Для дискретных случайных величин закон распределения вероятностей может быть задан: 1.
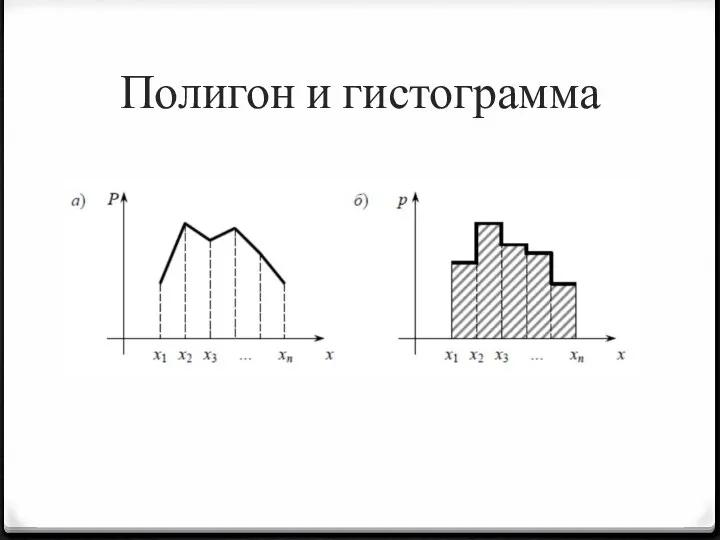
- 29. Законы распределения вероятностей случайных величин 2. В графической форме — в виде полигона распределения вероятностей или
- 30. Полигон и гистограмма
- 31. Практическое занятие №1 Построить полигон распределения времени колебаний для маятника № 1. Для этого в таблице
- 32. Практическое занятие №1 Таблица Построение полигона распределения времени колебаний маятника В случае, когда ti совпадает с
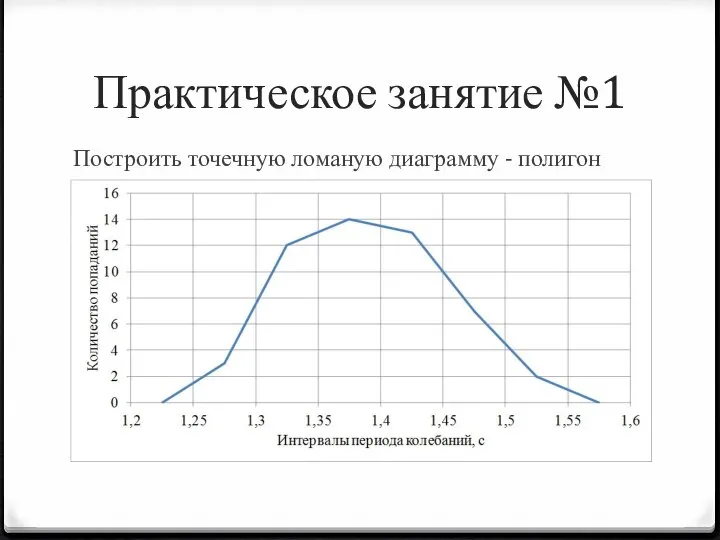
- 33. Практическое занятие №1 Построить точечную ломаную диаграмму - полигон
- 35. Скачать презентацию

![Основные положения Как получить достоверные знания? - пассивно-созерцательная теория Дидро [2] (главное](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1003644/slide-2.jpg)



























 Математическая игра Гусеница
Математическая игра Гусеница Тройные интегралы в цилиндрических координатах
Тройные интегралы в цилиндрических координатах РўР’РёРњРЎ_Лекция 3_Повторные независимые испытания
РўР’РёРњРЎ_Лекция 3_Повторные независимые испытания Свойства степени
Свойства степени Логарифмы. Логарифм числа. Основное логарифмическое тождество. Основные свойства логарифма
Логарифмы. Логарифм числа. Основное логарифмическое тождество. Основные свойства логарифма Презентация на тему Счёт предметов (1 класс)
Презентация на тему Счёт предметов (1 класс)  Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Способы быстрого счета
Способы быстрого счета Отношения между понятиями. Сравнение объектов
Отношения между понятиями. Сравнение объектов Микрокалькулятор
Микрокалькулятор Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ  Действительный анализ. Теорема Лебега о предельном переходе под знаком интеграла
Действительный анализ. Теорема Лебега о предельном переходе под знаком интеграла Решение задач на параллельность прямых и плоскостей
Решение задач на параллельность прямых и плоскостей Презентация на тему Свойства четырехугольников
Презентация на тему Свойства четырехугольников  Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ 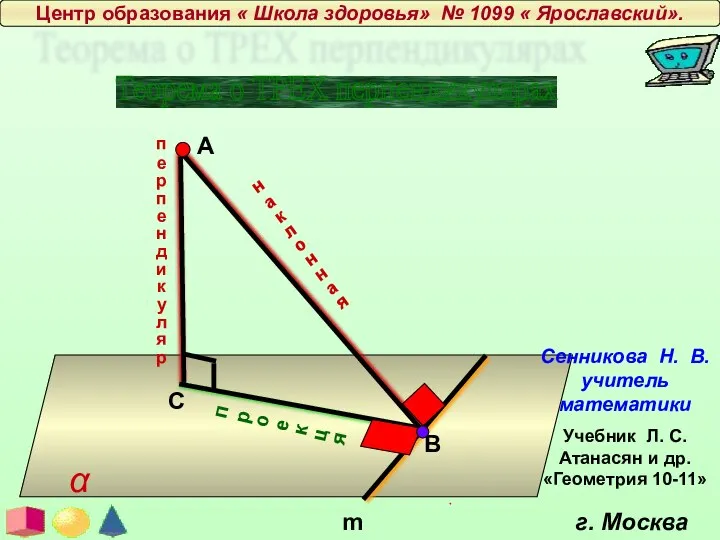 Теорема о трех перпендикулярах
Теорема о трех перпендикулярах Властивість бісектриси трикутника
Властивість бісектриси трикутника Многочлены от нескольких переменных
Многочлены от нескольких переменных Презентация на тему Призма. Построение сечений призмы плоскостями
Презентация на тему Призма. Построение сечений призмы плоскостями  Статистические сравнения
Статистические сравнения Из истории теоремы Пифагора
Из истории теоремы Пифагора 20140617_svoystva_funktsiy_9_klass
20140617_svoystva_funktsiy_9_klass Тригонометрические уравнения
Тригонометрические уравнения Влияние коэффициентов квадратного трехчлена на расположение параболы
Влияние коэффициентов квадратного трехчлена на расположение параболы Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах
Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах Длина
Длина Квадратные корни. Квадратные уравнения. 9 класс
Квадратные корни. Квадратные уравнения. 9 класс Понятие логарифма
Понятие логарифма