Метод корреляционных плеяд

Метод корреляционных плеяд
Цель:
сгруппировать признаки таким образом, чтобы признаки, попадающие в одну группу, признавались сильно связанными, а признаки, попадающие в разные группы – слабо связанными.
Зачем?
тогда, выбрав самые информативные признаки из каждой из групп, мы получим набор информативных и слабо связанных между собой признаков.
Метод состоит из двух этапов:
Построение графа взаимных связей признаков (по заданной матрице корреляционных взаимосвязей признаков)
Разбиение признаков на группы (по построенному графу взаимных связей признаков и заданному граничному значению для определения сильно связанных признаков)

Построение графа взаимных связей признаков
Пусть задана матрице корреляционных взаимосвязей признаков размерностью NхN (свойства: симметричная, по главной диагонали 1)
Алгоритм:
1. Находим в матрице максимальный недиагональный элемент.
2. Исходя из индексов найденного элемента, начинаем строить граф: индексы элемента определяют номера вершин графа, а значение найденного элемента – значение, которое наносят над ребром графа, которое соединяет эти вершины.
3. Рассматриваем две строки матрицы, номера которых соответствуют номерам двух последних рассмотренных вершин графа. В этих строках находим максимальный недиагональный элемент, не рассмотренный ранее
4. В матрице вычеркиваем строку и столбец с номерами, соответствующими номеру одной из двух последних рассмотренных строк графа, в которой НЕ НАШЛИ максимальный недиагональный элемент не рассмотренный ранее.
5. Исходя из индексов найденного элемента строим очередную часть графа: индексы элемента определяют номера вершин графа, а значение найденного элемента – значение, которое наносят над ребром графа, которое соединяет эти вершины.
6. Если количество вершин графа равно N, граф построен. Если нет – переходим к п.3.

Разбиение признаков на группы
После того как граф взаимных связей признаков построен, разбиваем признаки на группы:
«Разрываем» ребра графа, над которыми указаны значения, меньшие заданного граничного значения и смотрим, какие вершины графа остались связанными.

Задача:
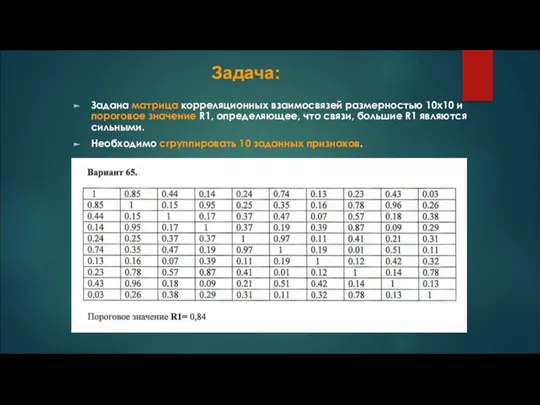
Задана матрица корреляционных взаимосвязей размерностью 10х10 и пороговое значение R1, определяющее, что связи, большие R1 являются сильными.
Необходимо сгруппировать 10 заданных признаков.

Решение задачи
1. Находим в матрице максимальный недиагональный элемент.
Этот элемент равен 0,97. Он показывает взаимосвязь признаков 5 и 6.

Решение задачи
2. Исходя из индексов найденного элемента (5 и 6), начинаем строить граф: индексы элемента определяют номера вершин графа, а значение найденного элемента (0,97) – значение, которое наносят над ребром графа, которое соединяет эти вершины.

Решение задачи
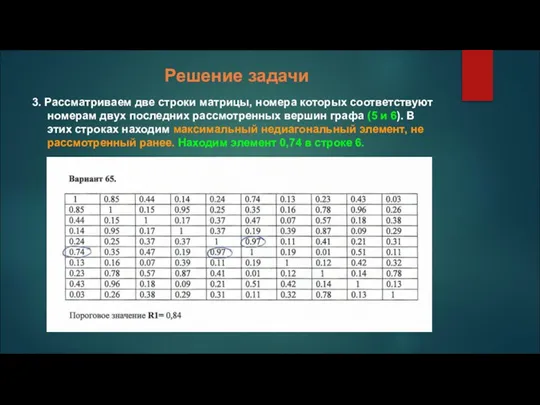
3. Рассматриваем две строки матрицы, номера которых соответствуют номерам двух последних рассмотренных вершин графа (5 и 6). В этих строках находим максимальный недиагональный элемент, не рассмотренный ранее. Находим элемент 0,74 в строке 6.

Решение задачи
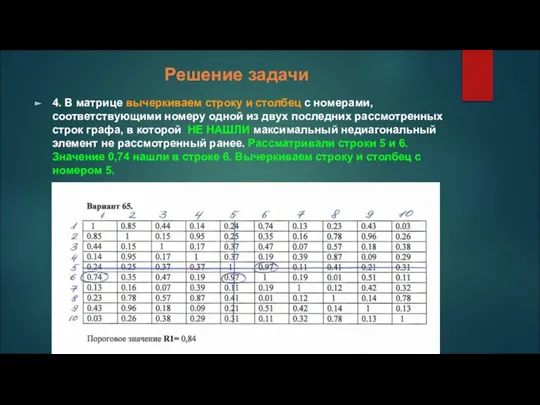
4. В матрице вычеркиваем строку и столбец с номерами, соответствующими номеру одной из двух последних рассмотренных строк графа, в которой НЕ НАШЛИ максимальный недиагональный элемент не рассмотренный ранее. Рассматривали строки 5 и 6. Значение 0,74 нашли в строке 6. Вычеркиваем строку и столбец с номером 5.

Решение задачи
5. Исходя из индексов найденного элемента строим очередную часть графа: индексы элемента определяют номера вершин графа, а значение найденного элемента – значение, которое наносят над ребром графа, которое соединяет эти вершины.
Элемент 0,74 соединяет признаки 6 и 1, добавляем в граф вершину 1 и соединяем ее с вершиной 6 ребром, над которым пишем 0,74.
6. Если количество вершин графа равно N, граф построен. Если нет – переходим к п.3.
Количество наших вершин равно 3. Переходим к п.3.

Решение задачи
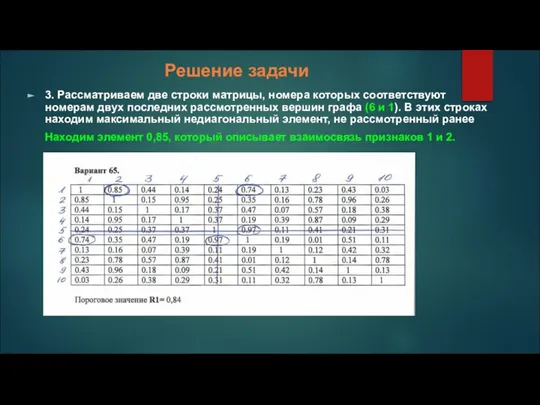
3. Рассматриваем две строки матрицы, номера которых соответствуют номерам двух последних рассмотренных вершин графа (6 и 1). В этих строках находим максимальный недиагональный элемент, не рассмотренный ранее
Находим элемент 0,85, который описывает взаимосвязь признаков 1 и 2.

Решение задачи
4. В матрице вычеркиваем строку и столбец с номерами, соответствующими номеру одной из двух последних рассмотренных строк графа, в которой НЕ НАШЛИ максимальный недиагональный элемент не рассмотренный ранее. Рассматривали строки 1 и 6. Значение 0,85 нашли в строке 1. Вычеркиваем строку и столбец с номером 6.

Решение задачи
5. Исходя из индексов найденного элемента строим очередную часть графа: индексы элемента определяют номера вершин графа, а значение найденного элемента – значение, которое наносят над ребром графа, которое соединяет эти вершины.
К вершине 1 добавляем вершину 2, а над ребром, которое их соединяет, пишем 0,85.
6. Если количество вершин графа равно N, граф построен. Если нет – переходим к п.3.
Количество вершин нашего графа равно 4. Переходим к п.3.

Решение задачи
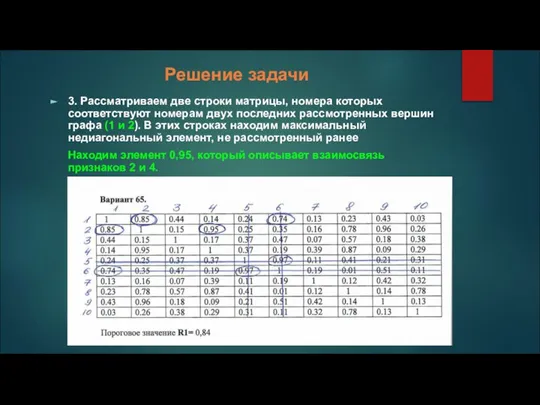
3. Рассматриваем две строки матрицы, номера которых соответствуют номерам двух последних рассмотренных вершин графа (1 и 2). В этих строках находим максимальный недиагональный элемент, не рассмотренный ранее
Находим элемент 0,95, который описывает взаимосвязь признаков 2 и 4.

Решение задачи
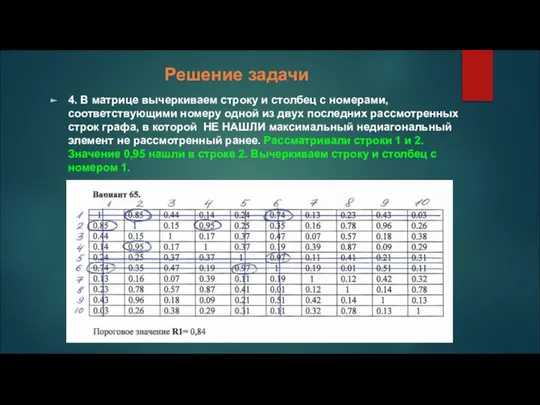
4. В матрице вычеркиваем строку и столбец с номерами, соответствующими номеру одной из двух последних рассмотренных строк графа, в которой НЕ НАШЛИ максимальный недиагональный элемент не рассмотренный ранее. Рассматривали строки 1 и 2. Значение 0,95 нашли в строке 2. Вычеркиваем строку и столбец с номером 1.

Решение задачи
5. Исходя из индексов найденного элемента строим очередную часть графа: индексы элемента определяют номера вершин графа, а значение найденного элемента – значение, которое наносят над ребром графа, которое соединяет эти вершины.
К вершине 2 добавляем вершину 4, а над ребром, которое их соединяет, пишем 0,95.
6. Если количество вершин графа равно N, граф построен. Если нет – переходим к п.3.
Количество вершин нашего графа равно 5. Переходим к п.3.

Решение задачи
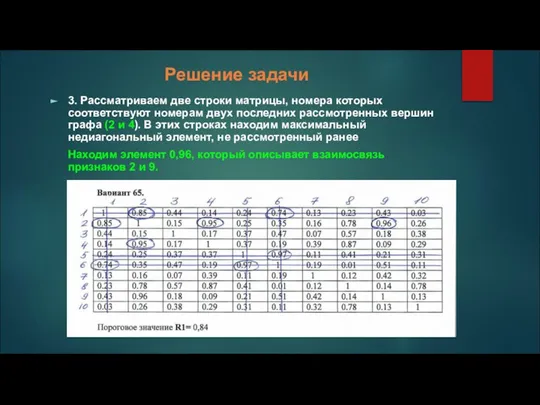
3. Рассматриваем две строки матрицы, номера которых соответствуют номерам двух последних рассмотренных вершин графа (2 и 4). В этих строках находим максимальный недиагональный элемент, не рассмотренный ранее
Находим элемент 0,96, который описывает взаимосвязь признаков 2 и 9.

Решение задачи
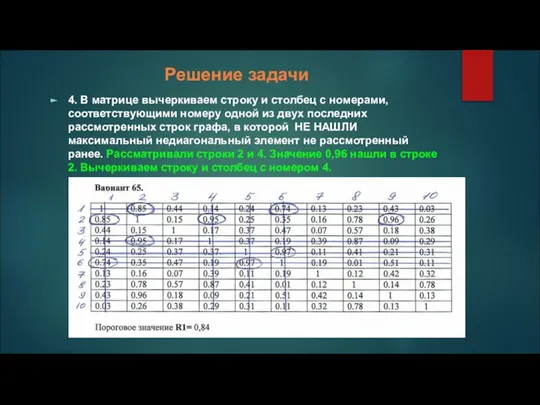
4. В матрице вычеркиваем строку и столбец с номерами, соответствующими номеру одной из двух последних рассмотренных строк графа, в которой НЕ НАШЛИ максимальный недиагональный элемент не рассмотренный ранее. Рассматривали строки 2 и 4. Значение 0,96 нашли в строке 2. Вычеркиваем строку и столбец с номером 4.

Решение задачи
5. Исходя из индексов найденного элемента строим очередную часть графа: индексы элемента определяют номера вершин графа, а значение найденного элемента – значение, которое наносят над ребром графа, которое соединяет эти вершины.
К вершине 2 добавляем вершину 9, а над ребром, которое их соединяет, пишем 0,96.
6. Если количество вершин графа равно N, граф построен. Если нет – переходим к п.3.
Количество вершин нашего графа равно 6. Переходим к п.3.

Решение задачи
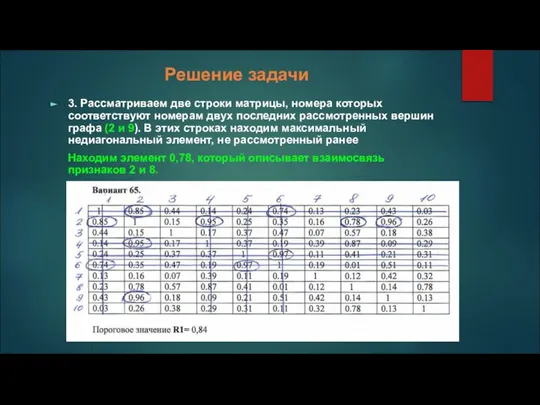
3. Рассматриваем две строки матрицы, номера которых соответствуют номерам двух последних рассмотренных вершин графа (2 и 9). В этих строках находим максимальный недиагональный элемент, не рассмотренный ранее
Находим элемент 0,78, который описывает взаимосвязь признаков 2 и 8.

Решение задачи
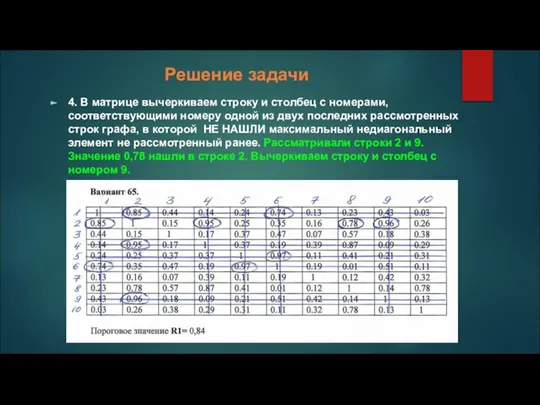
4. В матрице вычеркиваем строку и столбец с номерами, соответствующими номеру одной из двух последних рассмотренных строк графа, в которой НЕ НАШЛИ максимальный недиагональный элемент не рассмотренный ранее. Рассматривали строки 2 и 9. Значение 0,78 нашли в строке 2. Вычеркиваем строку и столбец с номером 9.

Решение задачи
5. Исходя из индексов найденного элемента строим очередную часть графа: индексы элемента определяют номера вершин графа, а значение найденного элемента – значение, которое наносят над ребром графа, которое соединяет эти вершины.
К вершине 2 добавляем вершину 8, а над ребром, которое их соединяет, пишем 0,78.
6. Если количество вершин графа равно N, граф построен. Если нет – переходим к п.3.
Количество вершин нашего графа равно 7. Переходим к п.3.

Решение задачи
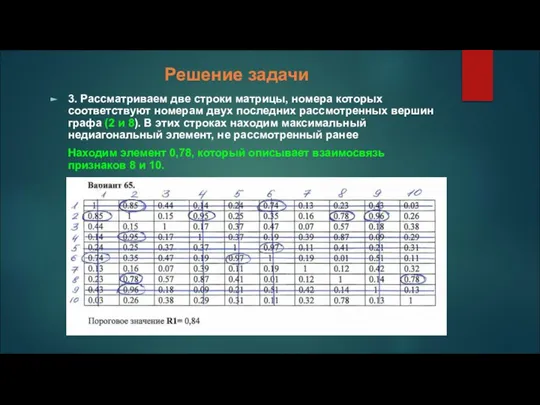
3. Рассматриваем две строки матрицы, номера которых соответствуют номерам двух последних рассмотренных вершин графа (2 и 8). В этих строках находим максимальный недиагональный элемент, не рассмотренный ранее
Находим элемент 0,78, который описывает взаимосвязь признаков 8 и 10.

Решение задачи
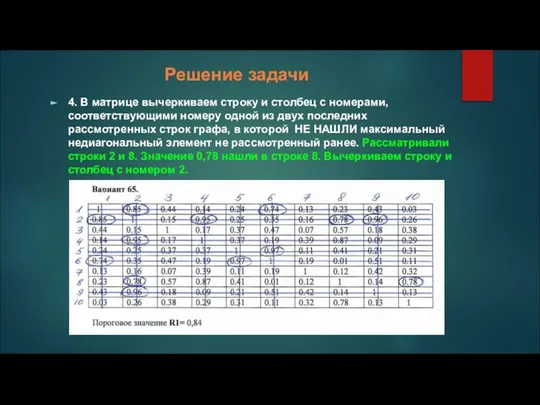
4. В матрице вычеркиваем строку и столбец с номерами, соответствующими номеру одной из двух последних рассмотренных строк графа, в которой НЕ НАШЛИ максимальный недиагональный элемент не рассмотренный ранее. Рассматривали строки 2 и 8. Значение 0,78 нашли в строке 8. Вычеркиваем строку и столбец с номером 2.

Решение задачи
5. Исходя из индексов найденного элемента строим очередную часть графа: индексы элемента определяют номера вершин графа, а значение найденного элемента – значение, которое наносят над ребром графа, которое соединяет эти вершины.
К вершине 8 добавляем вершину 10, а над ребром, которое их соединяет, пишем 0,78.
6. Если количество вершин графа равно N, граф построен. Если нет – переходим к п.3.
Количество вершин нашего графа равно 8. Переходим к п.3.

Решение задачи
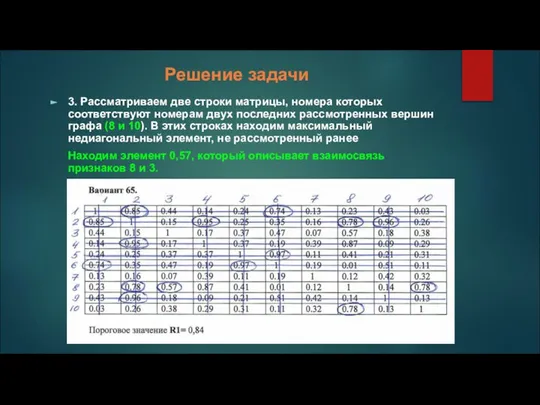
3. Рассматриваем две строки матрицы, номера которых соответствуют номерам двух последних рассмотренных вершин графа (8 и 10). В этих строках находим максимальный недиагональный элемент, не рассмотренный ранее
Находим элемент 0,57, который описывает взаимосвязь признаков 8 и 3.

Решение задачи
4. В матрице вычеркиваем строку и столбец с номерами, соответствующими номеру одной из двух последних рассмотренных строк графа, в которой НЕ НАШЛИ максимальный недиагональный элемент не рассмотренный ранее. Рассматривали строки 8 и 10. Значение 0,57 нашли в строке 8. Вычеркиваем строку и столбец с номером 10.

Решение задачи
5. Исходя из индексов найденного элемента строим очередную часть графа: индексы элемента определяют номера вершин графа, а значение найденного элемента – значение, которое наносят над ребром графа, которое соединяет эти вершины.
К вершине 8 добавляем вершину 3, а над ребром, которое их соединяет, пишем 0,57.
6. Если количество вершин графа равно N, граф построен. Если нет – переходим к п.3.
Количество вершин нашего графа равно 9. Переходим к п.3.

Решение задачи
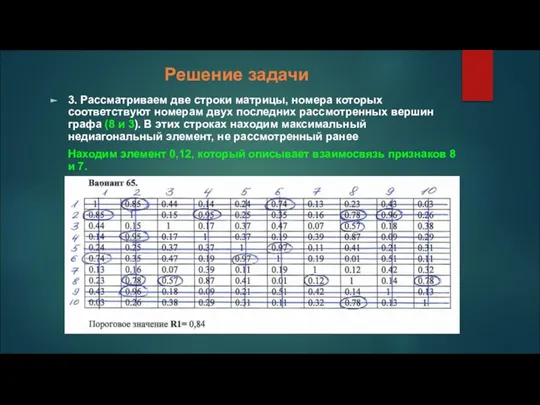
3. Рассматриваем две строки матрицы, номера которых соответствуют номерам двух последних рассмотренных вершин графа (8 и 3). В этих строках находим максимальный недиагональный элемент, не рассмотренный ранее
Находим элемент 0,12, который описывает взаимосвязь признаков 8 и 7.

Решение задачи
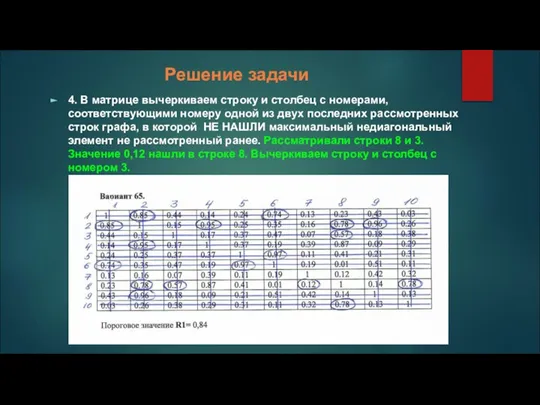
4. В матрице вычеркиваем строку и столбец с номерами, соответствующими номеру одной из двух последних рассмотренных строк графа, в которой НЕ НАШЛИ максимальный недиагональный элемент не рассмотренный ранее. Рассматривали строки 8 и 3. Значение 0,12 нашли в строке 8. Вычеркиваем строку и столбец с номером 3.

Решение задачи
5. Исходя из индексов найденного элемента строим очередную часть графа: индексы элемента определяют номера вершин графа, а значение найденного элемента – значение, которое наносят над ребром графа, которое соединяет эти вершины.
К вершине 8 добавляем вершину 7, а над ребром, которое их соединяет, пишем 0,12.
6. Если количество вершин графа равно N, граф построен. Если нет – переходим к п.3.
Количество вершин нашего графа равно 10. Граф построен.

Решение задачи
После того как граф взаимных связей признаков построен, разбиваем признаки на группы:
«Разрываем» ребра графа, над которыми указаны значения, меньшие заданного граничного значения и смотрим, какие вершины графа остались связанными.
R1= 0,84

Решение задачи
Ответ:
Группа 1: признаки 5 и 6
Группа 2: признаки 1, 2, 4, 9
Группа 3: признак 8
Группа 4: признак 3
Группа 5: признак 7
Группа 6: признак 10

Решение задачи
Группировка признаков сильно зависит от заданного граничного значения. При другом значении R2=0,72
R2=0,72
Ответ:
Группа 1: признаки 5, 6, 1, 2, 4, 9, 8, 10
Группа 2: признак 3
Группа 3: признак 7

Решение задачи
Таким образом, применив метод корреляционных плеяд, становится возможным группировка признаков таким образом, чтобы признаки, попадающие в одну группу, признавались сильно связанными, а признаки, попадающие в разные группы – слабо связанными.
Теперь, имея оценки информативности признаков для решения задачи распознавания (классификации), следует оставить от каждой группы только один самый информативный (в группе) признак. Набор отобранных таким образом наиболее информативных групповых признаков является основой для построения информативного признакового пространства для решения задачи распознавания (классификации). При необходимости построить признаковое пространство из 2-х или 3-х признаков следует выбрать указанное количество наиболее информативных признаков из набора отобранных ранее наиболее информативных групповых признаков.