Слайд 4Эллипс
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из

которых до двух данных точек этой плоскости , называется фокусами, есть величина постоянная, большая , чем расстояние фокуса
Слайд 5Каноническое уравнение эллипса

Слайд 6Дополнительные сведения об эллипсе

Слайд 8Гипербола
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой

из которых равен до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая чем расстояния между фокусами
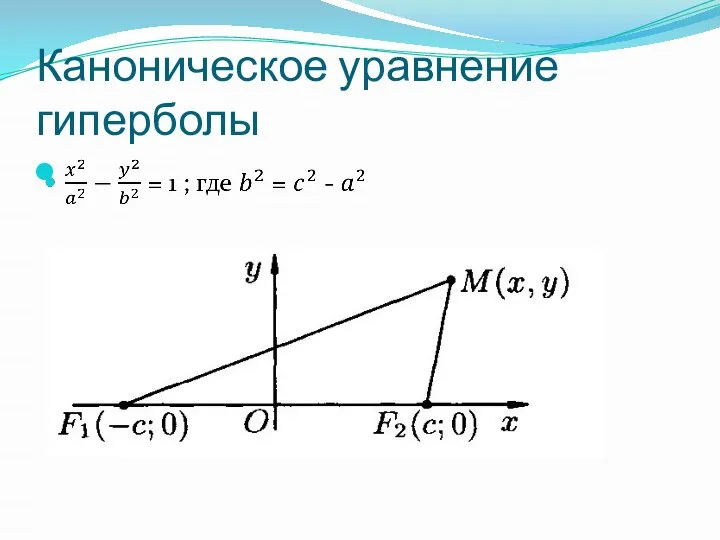
Слайд 9Каноническое уравнение гиперболы
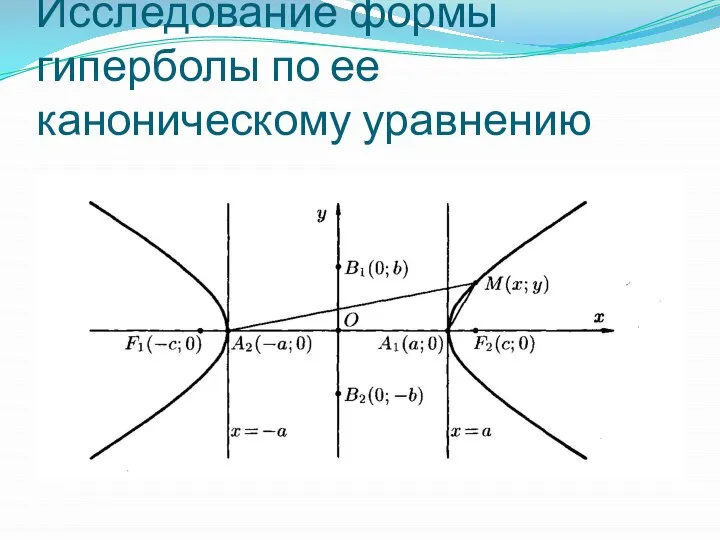
Слайд 10Исследование формы гиперболы по ее каноническому уравнению
Слайд 11Асимптоты гиперболы
Прямая L называется асимптотой неограниченной кривой K, если расстояние d

от точки M кривой K до этой прямой стремится к нулю при неограниченном удалении точки M вдоль кривой K от начала координат
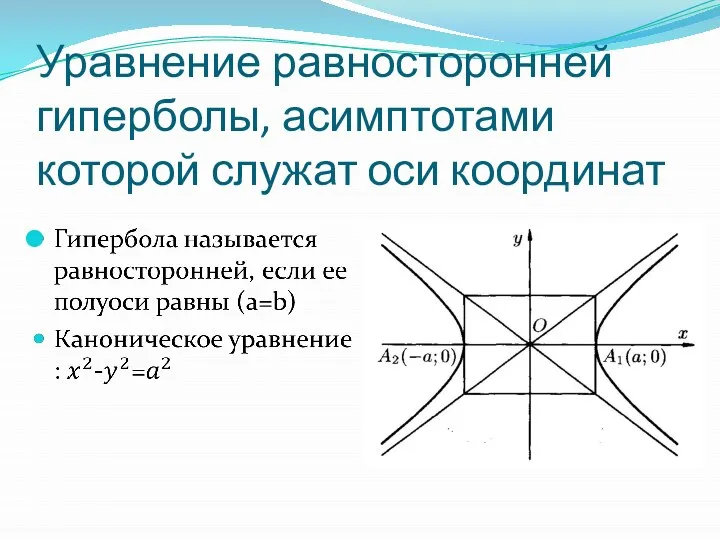
Слайд 12Уравнение равносторонней гиперболы, асимптотами которой служат оси координат
Слайд 13Дополнительные сведения о гиперболе

Слайд 14Парабола
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена
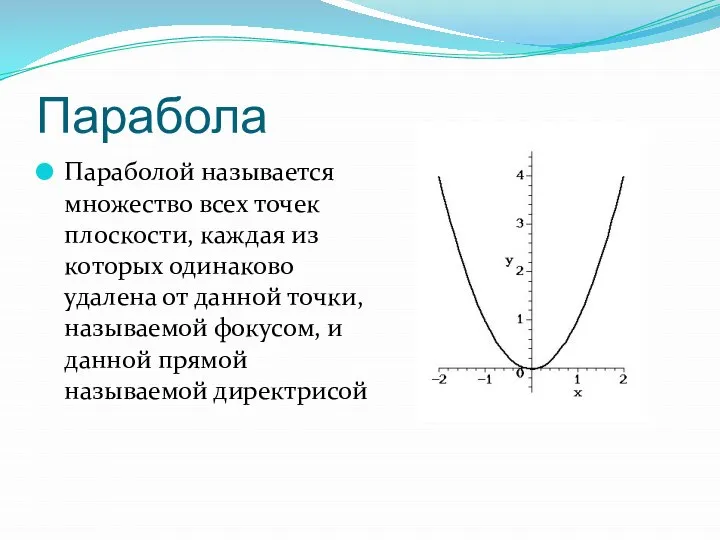
от данной точки, называемой фокусом, и данной прямой называемой директрисой
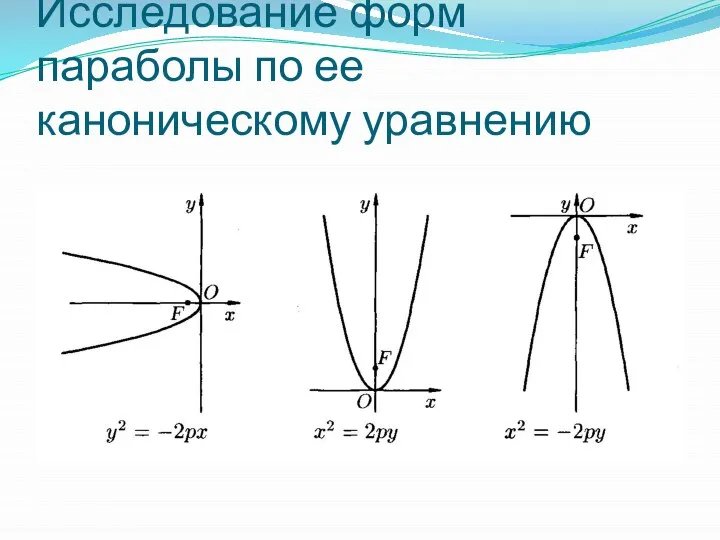
Слайд 16Исследование форм параболы по ее каноническому уравнению















 ЕГЭ. Экономические задачи VII
ЕГЭ. Экономические задачи VII Презентация на тему Решение систем уравнений
Презентация на тему Решение систем уравнений  Презентация на тему Объём многогранника
Презентация на тему Объём многогранника  Признаки равенства треугольников
Признаки равенства треугольников 3D моделирование на уроках стереометрии
3D моделирование на уроках стереометрии Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 15
Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 15 Презентация на тему Показательная функция и ее свойства
Презентация на тему Показательная функция и ее свойства  Многогранники. Призма
Многогранники. Призма Ментальная арифметика
Ментальная арифметика Построения графиков тригонометрических функций
Построения графиков тригонометрических функций Памятка по оформлению краткой записи к задачам (1 класс)
Памятка по оформлению краткой записи к задачам (1 класс) Моделирование в среде МАTLAB
Моделирование в среде МАTLAB Аналитическая геометрия на плоскости (лекция 1-2)
Аналитическая геометрия на плоскости (лекция 1-2) Презентация на тему Начертательная геометрия
Презентация на тему Начертательная геометрия  Системы массового обслуживания (СМО)
Системы массового обслуживания (СМО) Урок №19 Аналіз самостійної роботи. Розв’язування вправ
Урок №19 Аналіз самостійної роботи. Розв’язування вправ Матрицы и определители
Матрицы и определители Уравнения и неравенства с параметрами. 11 класс
Уравнения и неравенства с параметрами. 11 класс Треугольники. Решение задач
Треугольники. Решение задач Повторение Обыкновенные дроби. Основное свойство дроби. Из частного (деления) Дробной чертой Числитель Знаменатель Сравни
Повторение Обыкновенные дроби. Основное свойство дроби. Из частного (деления) Дробной чертой Числитель Знаменатель Сравни Контент-анализ на тему: Компаративный анализ популярных новогодних сказок в России
Контент-анализ на тему: Компаративный анализ популярных новогодних сказок в России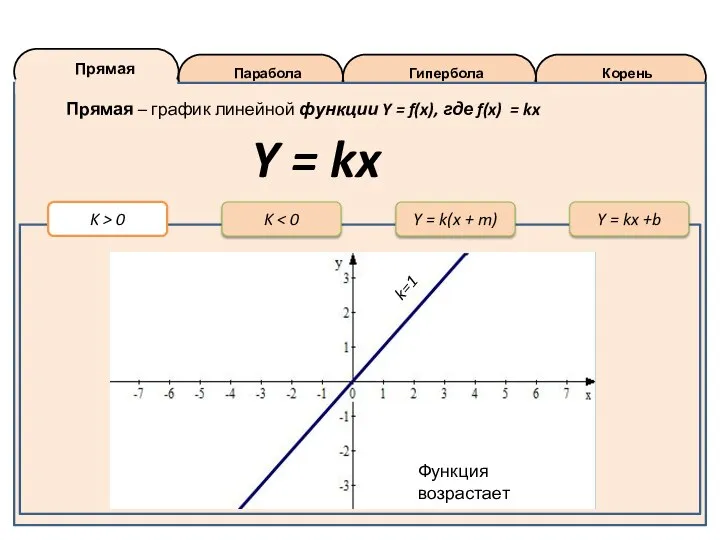 Прямая. Парабола. Гипербола. Корень
Прямая. Парабола. Гипербола. Корень Презентация на тему Фалес Милетский
Презентация на тему Фалес Милетский  Сложение чисел. Тренажер, 1 класс
Сложение чисел. Тренажер, 1 класс Устный счет. Действия с числами
Устный счет. Действия с числами Презентация на тему КВАДРАТИЧНАЯ ФУНКЦИЯ И КВАДРАТИЧНЫЕ НЕРАВЕНСТВА
Презентация на тему КВАДРАТИЧНАЯ ФУНКЦИЯ И КВАДРАТИЧНЫЕ НЕРАВЕНСТВА  Вероятность случайного события
Вероятность случайного события Квадратичная функция (8 класс)
Квадратичная функция (8 класс)