Содержание
- 2. Метод математической индукции – это способ доказательства справедливости утверждения на множестве чисел
- 3. Пример утверждения Представьте себе множество, допустим N – натуральных чисел (0, 1, 2, 3,… и т.д.)
- 4. Для того, чтобы доказать что-либо методом математической индукции, вам потребуется доказать БАЗУ ИНДУКЦИИ ШАГ ИНДУКЦИИ Вообще,
- 5. База индукции - это число, начиная с которого вы хотите доказывать верность утверждения. Например здесь, это
- 6. Давайте же докажем базу индукции. Применим нашу формулу для 1. Здесь n=1 так как наша конечная
- 7. Шаг индукции, простыми словами - это доказательство верности утверждения для числа K, опираясь на предположение, что
- 8. Итак, предполагая, что для n = (k - 1) наше утверждение верное, докажем, что утверждение верно
- 9. ((1+(k-1))/2)*(k-1)+k Преобразуем это выражение (k/2)*(k-1)+k ((k*k)/2)-(k/2))+k k*k/2+k/2 (1/2)(k*k+k) (1/2)k(k+1) ((1+k)/2)*k – вот мы и пришли к
- 10. После этого может всё равно остаться вопрос, типо, почему это работает? Для устранения этого непонимания я
- 11. P(i) ложное (утверждение для n = i не работает) Тогда поступим следующим образом: Так как i
- 12. В качестве хорошего материала для практического понимания могу предложить этот видеоролик. Мне в своё время он
- 14. Скачать презентацию











 Виды графов
Виды графов Тройные интегралы в цилиндрических координатах
Тройные интегралы в цилиндрических координатах Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе
Соотношения между сторонами и углами треугольника. Подготовка к контрольной работе Китайская математика
Китайская математика Дополнительные задачи. 7 класс
Дополнительные задачи. 7 класс Множители и произведение
Множители и произведение Математика учит точности мысли
Математика учит точности мысли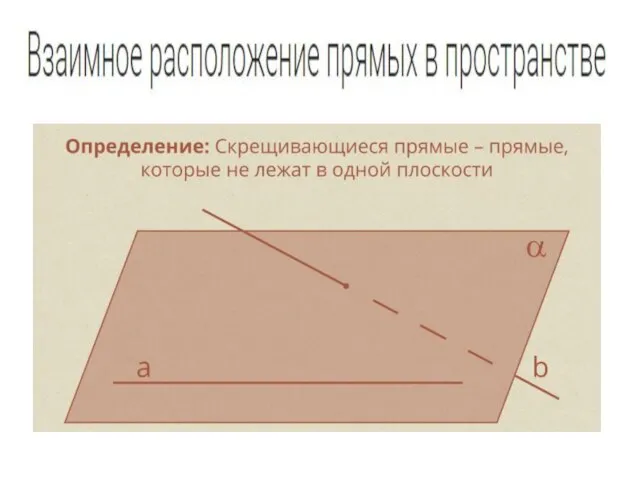 Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Подбираем наибольшее произведение
Подбираем наибольшее произведение В мире геометрии
В мире геометрии Элементы комбинаторики
Элементы комбинаторики Простейшие задачи в координатах
Простейшие задачи в координатах Цифровые устройства. Логические функции и их минимизация
Цифровые устройства. Логические функции и их минимизация Линейные пространства и подпространства
Линейные пространства и подпространства Простейшие задачи в координатах
Простейшие задачи в координатах Задачи на проценты
Задачи на проценты Площадь треугольника
Площадь треугольника Презентация на тему История теоремы Пифагора
Презентация на тему История теоремы Пифагора  Частные производные второго порядка
Частные производные второго порядка Проценты в медицине
Проценты в медицине Сложение с переходом через десяток
Сложение с переходом через десяток Сходимость последовательности СВ
Сходимость последовательности СВ Квадратные уравнения
Квадратные уравнения Предел последовательности. Практическая работа № 24
Предел последовательности. Практическая работа № 24 Моделирование в технике
Моделирование в технике Пропорциональность отрезков хорд и секущих окружности
Пропорциональность отрезков хорд и секущих окружности Элементы комбинаторики
Элементы комбинаторики Закон больших чисел и предельные теоремы
Закон больших чисел и предельные теоремы