Содержание
- 2. Для дифференцируемой в точке х0 функции f при Δх, мало отличающихся от нуля, её график близок
- 3. Формула f(х) ≈f(х 0)+f‘(х0)Δх позволяет вывести следующие формулы для приближённых вычислений 1) 1+Δх≈1+1/2Δх 2) (1+Δх)n≈1+nΔx
- 4. 1,06= 1+0,06≈1+1/2*0,06=1,03 Вычислим по формуле(1) 1+Δх≈1+1/2Δх значение выражения 1,06 Решение: Δх=0,06
- 6. Скачать презентацию



 Построение графиков функций элементарными средствами
Построение графиков функций элементарными средствами Умножаем на 4
Умножаем на 4 Основы геометрии
Основы геометрии Обработка экспериментальных данных. Описательная статистика: основные понятия
Обработка экспериментальных данных. Описательная статистика: основные понятия Презентация на тему Наибольший общий делитель
Презентация на тему Наибольший общий делитель  Индивидуальные задания. Урок 15
Индивидуальные задания. Урок 15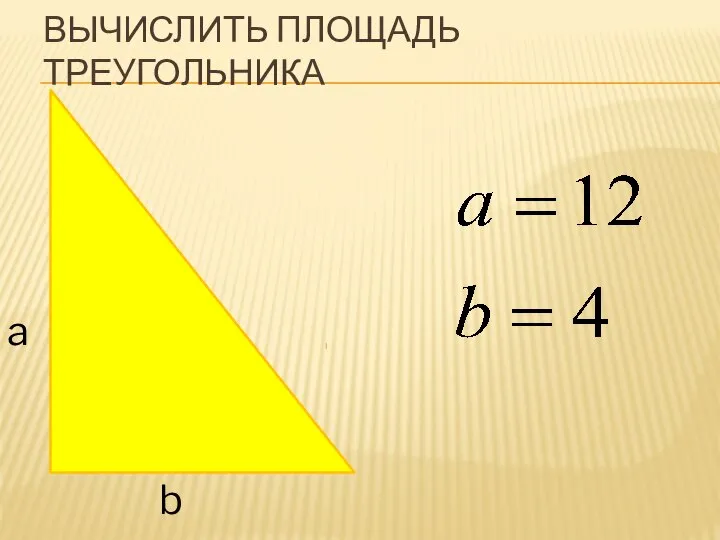 Вычисление площади треугольника
Вычисление площади треугольника Числа 1 - 4. (1 класс)
Числа 1 - 4. (1 класс) Презентация на тему Плоскость. Прямая. Луч
Презентация на тему Плоскость. Прямая. Луч  Осевая симметрия
Осевая симметрия Самостоятельная работа по производным
Самостоятельная работа по производным Найти точки экстремума функции
Найти точки экстремума функции Первообразная и интеграл
Первообразная и интеграл Признаки параллелограмма
Признаки параллелограмма Подобные треугольники. (8 класс)
Подобные треугольники. (8 класс) Прямоугольный треугольник. Теоремы и определения
Прямоугольный треугольник. Теоремы и определения Целые и дробные числа
Целые и дробные числа Презентация на тему Измерение углов
Презентация на тему Измерение углов  Составление и решение текстовых задач на увеличение и уменьшение числа на несколько единиц
Составление и решение текстовых задач на увеличение и уменьшение числа на несколько единиц Простейшие линейные цепи при гармоническом воздействии
Простейшие линейные цепи при гармоническом воздействии Основные законы теории вероятности
Основные законы теории вероятности Предел функции (часть 4)
Предел функции (часть 4) Презентация на тему Правильные выпуклые многогранники
Презентация на тему Правильные выпуклые многогранники  Увлекательный мир умножения
Увлекательный мир умножения Открытый банк заданий ЕГЭ по математике
Открытый банк заданий ЕГЭ по математике Деление с остатком. Решение задач
Деление с остатком. Решение задач Презентация на тему РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Презентация на тему РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ  Числовые промежутки. Пересечение и объединение промежутков
Числовые промежутки. Пересечение и объединение промежутков