Metode numerice. Mulţimea F, de numere în virgulă mobilă este. Curs13

METODE NUMERICE – curs 13

METODE NUMERICE – curs 13
fl(x – y + z) = 0 + fl(z) = fl(z) = (0.11110)2 x 21
neutralizarea termenilor
rearanjarea calculelor pentru evitarea neutralizării termenilor:
fl(x + z - y) = fl( fl(x + z) - y)
fl(x + z) = (0.10001)2 x 24 + (0.11110)2 x 21 = (0.10001)2 x 24 + (0.00011110)2 x 24
fl(x + z) = (0.10100)2 x 24
fl(x + z - y) = fl(x+z) – fl(y) = (0.10100)2 x 24 - (0.10001)2 x 24 = (0.00011)2 x 24 = (0.11000)2 x 21
normalizare

METODE NUMERICE – curs 13

METODE NUMERICE – curs 13
fl(x + y - z) = fl( fl(x + y) - z)
fl(x + y) = (0.10110)2 x 23 + (0.10011)2 x 2-2 = (0.10110)2 x 23 + (0.0000010011)2 x 23 = (0.10110)2 x 23
omitere catastrofală
fl(x + y - z) = (0.10110)2 x 23 - fl(z) = (0.10110)2 x 23 - (0.10110)2 x 23 = 0
neutralizarea termenilor
rearanjarea calculelor pentru evitarea neutralizării termenilor → nu este posibilă

✍ Exerciţiul 3
Argumentaţi, pornind de la definiţie, că un algoritm instabil numeric produce, de regulă, rezultate eronate chiar dacă problema de calcul este bine condiţionată.
Rezolvare:
Notații:
D/ D* - date de intrare exacte/ ușor perturbate;
G/ G* - problema de calcul/ algoritm de rezolvare a problemei de calcul
Definiții:
Algoritm instabil → D*≅ D astfel încât G(D*) ≠ G*(D)
Problemă bine condiționată: D*≅ D ⇒ G(D) ≅ G(D*)
METODE NUMERICE – curs 13
⇓
D*≅ D astfel încât G(D) ≠ G*(D)

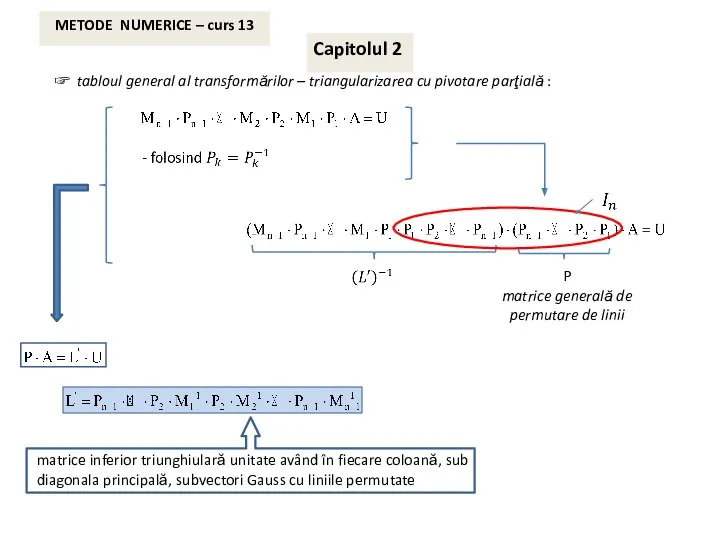
☞ tabloul general al transformărilor – triangularizarea cu pivotare parţială :
P
matrice generală de permutare de linii
METODE NUMERICE – curs 13
Capitolul 2

☞ Metoda Jacobi şi metoda Gauss-Seidel :
METODE NUMERICE – curs 13
⮞ metoda Jacobi
⮞ metoda Gauss-Seidel
Propoziţie:
Dacă matricea A este diagonal dominantă pe linii, atunci metoda Jacobi este convergentă, oricare ar fi estimaţia iniţială a soluţiei sistemului de ecuaţii.
⮞ Relaţia de recurenţă:
N - matrice nesingulară
⭢
Notaţie:
⮞ G are valori proprii în general complexe, care formează mulţimea numită spectrul matricei G
- rază spectrală a matricei G
Teoremă:
Condiţia necesară şi suficientă ca şirul de vectori să fie convergent către soluţia sistemului de ecuaţii este ca matricea G să aibă toate valorile proprii în modul subunitare sau, altfel spus, raza spectrală a matricei G să fie subunitară.

METODE NUMERICE – curs 13
✍ Exerciţiul 4
Calculaţi determinantul unei matrici ştiind că rezultatele factorizării sale L-U prin triangularizare cu pivotare parțială sunt:
Precizaţi care este pivotul la iteraţia a doua a triangularizării şi în ce linie şi în ce coloană se află. Argumentaţi.
Rezolvați sistemul determinat de ecuații algebrice liniare având matricea de coeficienți cu rezultatele factorizarii L_U date mai sus şi coloana termenilor liberi:
Rezolvare:
calcul determinant
P⋅A = L⋅U ⇒ A = P-1 ⋅L⋅U ⇒ det(A) = det(P-1) ⋅ det(L) ⋅ det(U) = (-1)npl ⋅det(U)
npl – număr de permutări de linii efectiv realizate → se determină din matricea P

METODE NUMERICE – curs 13

✍ Exerciţiul 5
Fie sistemul de ecuaţii algebrice liniare cu matricea de coeficienți:
METODE NUMERICE – curs 13
Precizaţi dacă metoda Gauss-Seidel poate fi aplicată pentru rezolvarea sistemului. Argumentaţi.
Rezolvare:
☞ verificare condiții convergență:
suficientă → matricea A să fie diagonal dominantă pe linii ⇒ nu este
necesară şi suficientă → raza spectrală a matricii G = N-1 ⋅ P - subunitară
metoda Gauss-Seidel poate fi aplicată pentru rezolvarea sistemului

METODE NUMERICE – curs 13
✍ Exerciţiul 6
Realizaţi funcția MATLAB ce returnează coeficienții calculați în sensul celor mai mici pătrate a ai dependenţei:
pe baza valorilor cunoscute stocate într-o matrice cu n linii şi 4 coloane. Se vor utiliza funcțiile elementare ale mediului MATLAB, precum şi funcția “ \ ”.
Rezolvare:
formare sistem supradeterminat:
- notație:
A
x
b
Capitolul 3

METODE NUMERICE – curs 13