Содержание
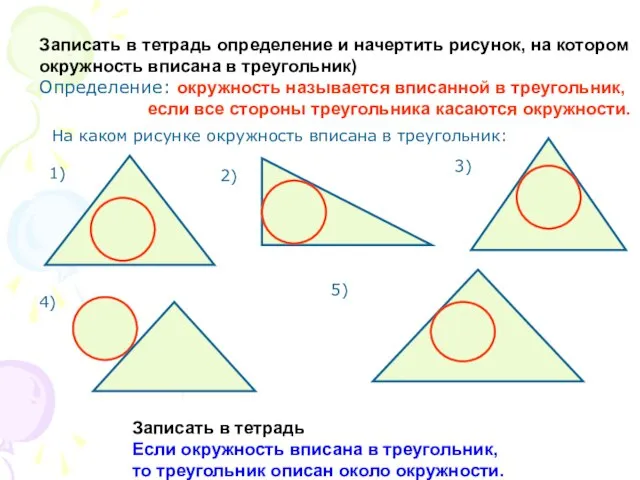
- 2. Записать в тетрадь определение и начертить рисунок, на котором окружность вписана в треугольник) Определение: окружность называется
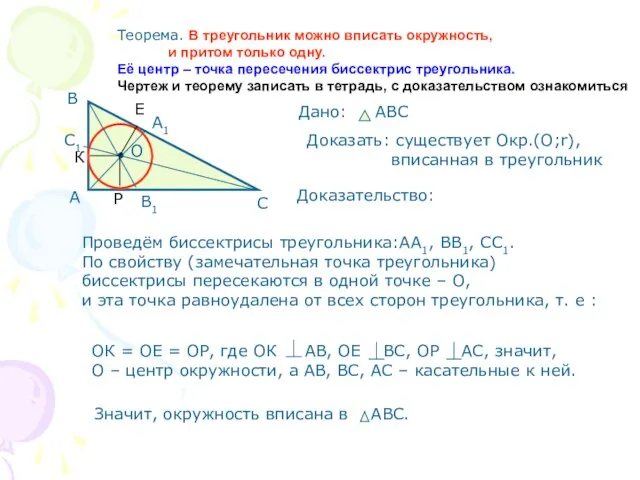
- 3. Теорема. В треугольник можно вписать окружность, и притом только одну. Её центр – точка пересечения биссектрис
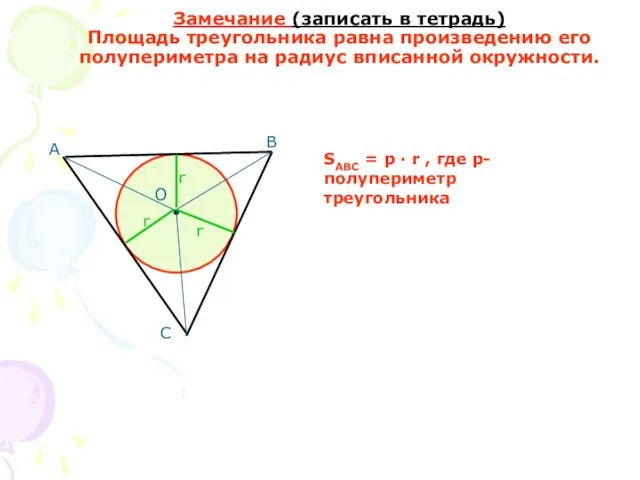
- 4. Замечание (записать в тетрадь) Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. SABC =
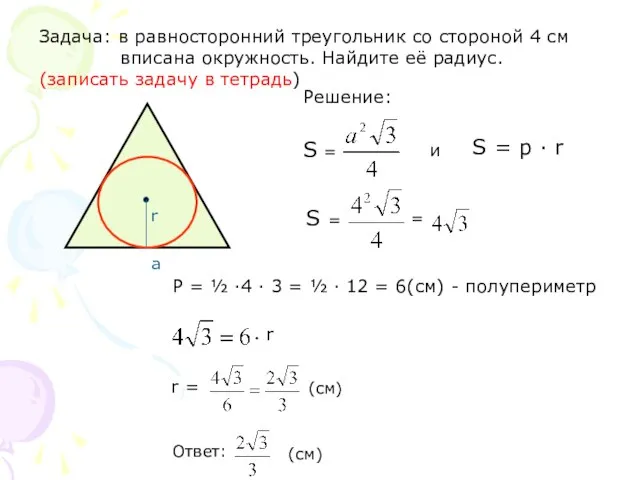
- 5. Задача: в равносторонний треугольник со стороной 4 см вписана окружность. Найдите её радиус. (записать задачу в
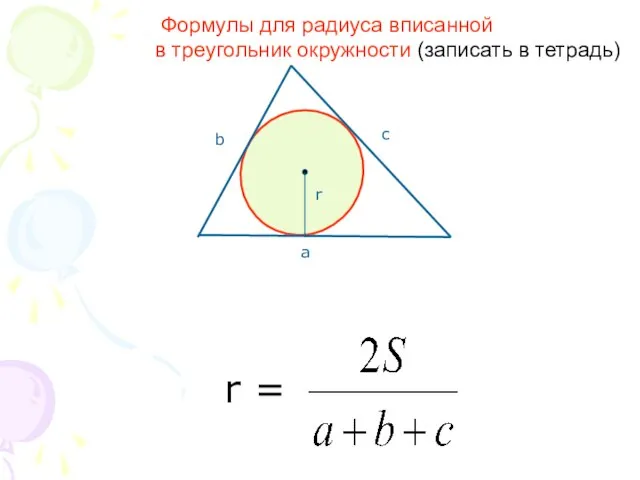
- 6. Формулы для радиуса вписанной в треугольник окружности (записать в тетрадь)
- 7. Задача: в прямоугольный треугольник вписана окружность, гипотенуза точкой касания делится на отрезки 6 см и 4
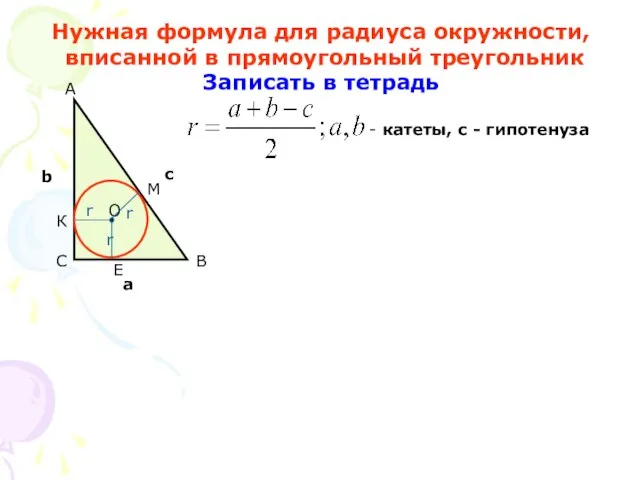
- 8. Нужная формула для радиуса окружности, вписанной в прямоугольный треугольник Записать в тетрадь
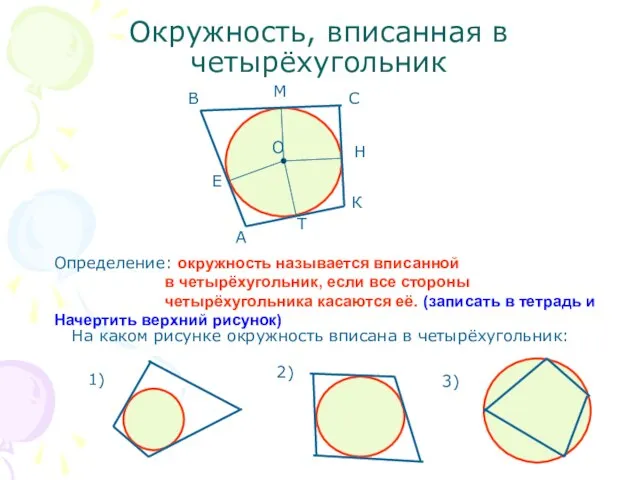
- 9. Окружность, вписанная в четырёхугольник Определение: окружность называется вписанной в четырёхугольник, если все стороны четырёхугольника касаются её.
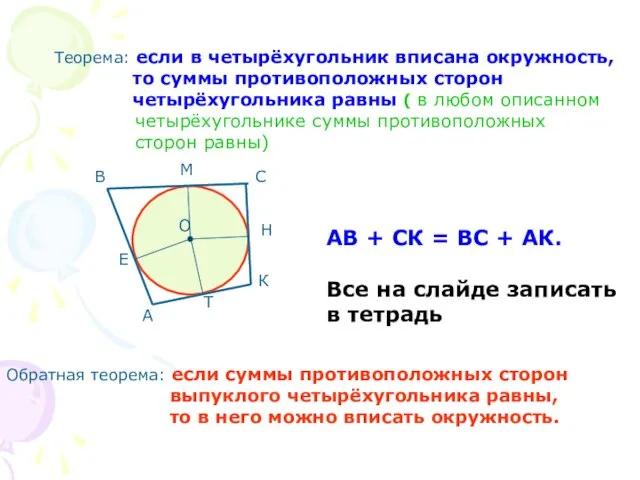
- 10. Теорема: если в четырёхугольник вписана окружность, то суммы противоположных сторон четырёхугольника равны ( в любом описанном
- 11. Задача: в ромб, острый угол которого 600, вписана окружность, радиус которой равен 2 см. Найти периметр
- 13. Скачать презентацию


 Бесконечные периодические десятичные дроби
Бесконечные периодические десятичные дроби Деление числа на десятичную дробь
Деление числа на десятичную дробь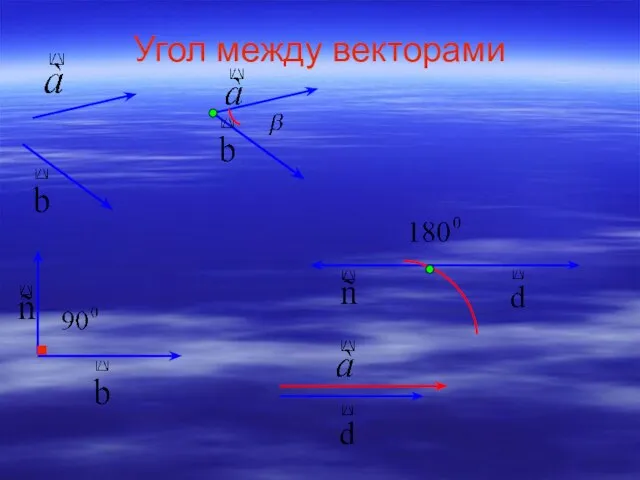 Презентация на тему Угол между векторами и скалярное произведение векторов
Презентация на тему Угол между векторами и скалярное произведение векторов  Решение задач
Решение задач Умножение и деление степеней
Умножение и деление степеней Вычисления с многозначными числами
Вычисления с многозначными числами Решение задач. 3 класс
Решение задач. 3 класс Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Сложение вида +2, +3
Сложение вида +2, +3 Производная сложной функции
Производная сложной функции Презентация на тему Координатная плоскость (7 класс)
Презентация на тему Координатная плоскость (7 класс)  Математическое моделирование. Рандомизация
Математическое моделирование. Рандомизация Презентация на тему Геометрические тела
Презентация на тему Геометрические тела  Начальные геометрические сведения. Признаки равенства треугольников
Начальные геометрические сведения. Признаки равенства треугольников Аксонометрические проекции плоских фигур
Аксонометрические проекции плоских фигур Комплексные числа. Понятие мнимой единицы. Алгебраическая форма комплексного числа. Задания
Комплексные числа. Понятие мнимой единицы. Алгебраическая форма комплексного числа. Задания Планиметрия и стериометрия
Планиметрия и стериометрия Решение задач
Решение задач Подготовка к контрольной работе
Подготовка к контрольной работе Презентация на тему Системы линейных уравнений с двумя переменными
Презентация на тему Системы линейных уравнений с двумя переменными  П 2
П 2 Презентация на тему Шутка гениев: флексагон
Презентация на тему Шутка гениев: флексагон  Умножение и деление десятичных дробей
Умножение и деление десятичных дробей Таблица сложения до 10
Таблица сложения до 10 Измерение углов поворота в радианах. Алгебра 9 класс
Измерение углов поворота в радианах. Алгебра 9 класс P-ичная арифметика. Решение задач
P-ичная арифметика. Решение задач Презентация на тему Перпендикуляр и наклонная 10 класс
Презентация на тему Перпендикуляр и наклонная 10 класс  ES_in_Diag
ES_in_Diag