Transformace. Ekvivalence

Transformace
Transformace je přepis formule pomocí ekvivalenčních pravidel do zápisu, který je jednodušší a vyjadřuje stejné pravdivostní podmínky.

Transformace
Transformace je přepis formule pomocí ekvivalenčních pravidel do zápisu, který je jednodušší a vyjadřuje stejné pravdivostní podmínky.
Než si ukážeme, jak probíhá postup takového přepisu, vysvětlíme si nejprve některé termíny:

Transformace
Transformace je přepis formule pomocí ekvivalenčních pravidel do zápisu, který je jednodušší a vyjadřuje stejné pravdivostní podmínky.
Než si ukážeme, jak probíhá postup takového přepisu, vysvětlíme si nejprve některé termíny:
Co to je ekvivalence a co to znamená, že dvě tvrzení jsou nebo nejsou ekvivalentní
Co to znamená, že formule vyjadřuje pravdivostní podmínky, a co to znamená, že jedny a ty samé pravdivostní podmínky mohou být vyjádřeny různými formulemi
Co to jsou ekvivalenční pravidla a co to znamená, že nějakou formuli podle těchto pravidel upravujeme.

Ekvivalence
Ekvivalence je základní logický vztah, který vyjadřuje, že dvě tvrzení mají stejné pravdivostní podmínky

Ekvivalence
Ekvivalence je základní logický vztah, který vyjadřuje, že dvě tvrzení mají stejné pravdivostní podmínky
jsou pravdivé (a nepravdivé) ve stejných situacích
jsou pravdivé stejným způsobem (stejně)
popisují stejné situace

Ekvivalence
Ekvivalence je základní logický vztah, který vyjadřuje, že dvě tvrzení mají stejné pravdivostní podmínky
jsou pravdivé (a nepravdivé) ve stejných situacích
jsou pravdivé stejným způsobem (stejně)
popisují stejné situace
Logický vztah ekvivalence je vyjádřen logickou spojkou ekvivalence

Ekvivalence
Ekvivalence je základní logický vztah, který vyjadřuje, že dvě tvrzení mají stejné pravdivostní podmínky
jsou pravdivé (a nepravdivé) ve stejných situacích
jsou pravdivé stejným způsobem (stejně)
popisují stejné situace
Logický vztah ekvivalence je vyjádřen logickou spojkou ekvivalence

Ekvivalence
Ekvivalence je základní logický vztah, který vyjadřuje, že dvě tvrzení mají stejné pravdivostní podmínky
jsou pravdivé (a nepravdivé) ve stejných situacích
jsou pravdivé stejným způsobem (stejně)
popisují stejné situace
Logický vztah ekvivalence je vyjádřen logickou spojkou ekvivalence
Ekvivalence je pravdivá, pokud oba její členy (obě věty, které spojuje)
mají stejné pravdivostní hodnoty

Ekvivalence
Vezměme následující dvě formule:

Ekvivalence
Vezměme následující dvě formule:
Liší se od sebe pořadím členů konjunkce

Ekvivalence
Vezměme následující dvě formule:
Liší se od sebe pořadím členů konjunkce
Tabulka ukazuje, že obě formule mají STEJNÉ pravdivostní podmínky

Ekvivalence
Vezměme následující dvě formule:
Liší se od sebe pořadím členů konjunkce
Tabulka ukazuje, že obě formule mají STEJNÉ pravdivostní podmínky
= JSOU ekvivalentní

Ekvivalence
Vezměme následující dvě formule:
Liší se od sebe pořadím členů konjunkce
Tabulka ukazuje, že obě formule mají STEJNÉ pravdivostní podmínky
= JSOU ekvivalentní

Ekvivalence
Vezměme následující dvě formule:
Liší se od sebe pořadím členů konjunkce
Tabulka ukazuje, že obě formule mají STEJNÉ pravdivostní podmínky
= JSOU ekvivalentní
Poznámka: V případě konjunkce (stejně jako u disjunkce a ekvivalence) na pořadí členů NEZÁLEŽÍ.

Ekvivalence
Vezměme následující dvě formule:
Liší se od sebe pořadím členů konjunkce
Tabulka ukazuje, že obě formule mají STEJNÉ pravdivostní podmínky
= JSOU ekvivalentní
Poznámka: V případě konjunkce (stejně jako u disjunkce a ekvivalence) na pořadí členů NEZÁLEŽÍ.
Tyto dvě formule se opět liší pouze pořadím členů implikace

Ekvivalence
Vezměme následující dvě formule:
Liší se od sebe pořadím členů konjunkce
Tabulka ukazuje, že obě formule mají STEJNÉ pravdivostní podmínky
= JSOU ekvivalentní
Poznámka: V případě konjunkce (stejně jako u disjunkce a ekvivalence) na pořadí členů NEZÁLEŽÍ.
Tyto dvě formule se opět liší pouze pořadím členů implikace
Tabulka tentokrát ale ukazuje, že mají RŮZNÉ pravdivostní podmínky.

Ekvivalence
Vezměme následující dvě formule:
Liší se od sebe pořadím členů konjunkce
Tabulka ukazuje, že obě formule mají STEJNÉ pravdivostní podmínky
= JSOU ekvivalentní
Poznámka: V případě konjunkce (stejně jako u disjunkce a ekvivalence) na pořadí členů NEZÁLEŽÍ.
Tyto dvě formule se opět liší pouze pořadím členů implikace
Tabulka tentokrát ale ukazuje, že mají RŮZNÉ pravdivostní podmínky.
= NEJSOU ekvivalentní

Ekvivalence
Vezměme následující dvě formule:
Liší se od sebe pořadím členů konjunkce
Tabulka ukazuje, že obě formule mají STEJNÉ pravdivostní podmínky
= JSOU ekvivalentní
Poznámka: V případě konjunkce (stejně jako u disjunkce a ekvivalence) na pořadí členů NEZÁLEŽÍ.
Tyto dvě formule se opět liší pouze pořadím členů implikace
Tabulka tentokrát ale ukazuje, že mají RŮZNÉ pravdivostní podmínky.
= NEJSOU ekvivalentní

Ekvivalence
Vezměme následující dvě formule:
Liší se od sebe pořadím členů konjunkce
Tabulka ukazuje, že obě formule mají STEJNÉ pravdivostní podmínky
= JSOU ekvivalentní
Poznámka: V případě konjunkce (stejně jako u disjunkce a ekvivalence) na pořadí členů NEZÁLEŽÍ.
Tyto dvě formule se opět liší pouze pořadím členů implikace
Tabulka tentokrát ale ukazuje, že mají RŮZNÉ pravdivostní podmínky.
= NEJSOU ekvivalentní
Poznámka: V případě implikace (na rozdíl od všech ostatních lg. spojek) na pořadí členů ZÁLEŽÍ.

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými způsoby (formulemi).

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými způsoby (formulemi).
Tady máme příklad dvou různých formulí, které jsou ekvivalentní

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými způsoby (formulemi).
Tady máme příklad dvou různých formulí, které jsou ekvivalentní
tabulka ukazuje, že mají stejné výsledné sloupce

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými způsoby (formulemi).
Tady máme příklad dvou různých formulí, které jsou ekvivalentní
tabulka ukazuje, že mají stejné výsledné sloupce
mají stejné pravdivostní podmínky
jsou pravdivé stejným způsobem
jsou pravdivé ve stejných situacích
popisují stejné situace

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými způsoby (formulemi).
Vidíme tedy, že

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými způsoby (formulemi).
Vidíme tedy, že
jedny a ty samé pravdivostní podmínky
jednu a tu samou situaci

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=
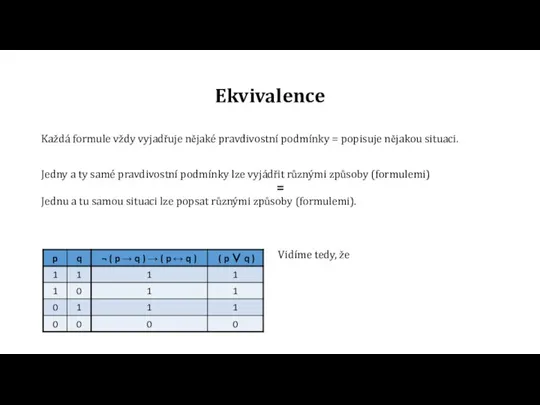
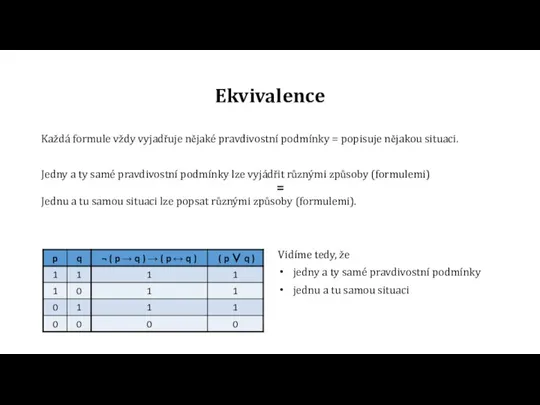
Jednu a tu samou situaci lze popsat různými způsoby (formulemi).
Vidíme tedy, že
jedny a ty samé pravdivostní podmínky
jednu a tu samou situaci
můžeme popsat různými způsoby

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=
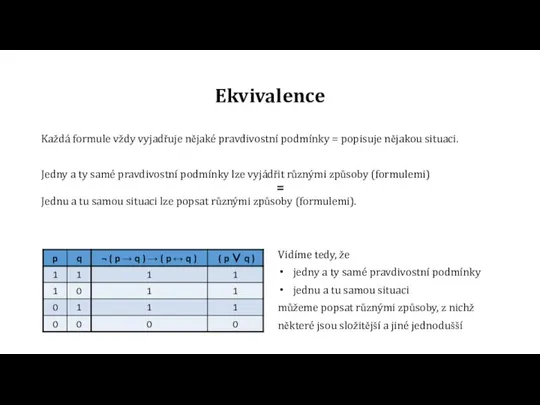
Jednu a tu samou situaci lze popsat různými způsoby (formulemi).
Vidíme tedy, že
jedny a ty samé pravdivostní podmínky
jednu a tu samou situaci
můžeme popsat různými způsoby, z nichž
některé jsou složitější a jiné jednodušší

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=
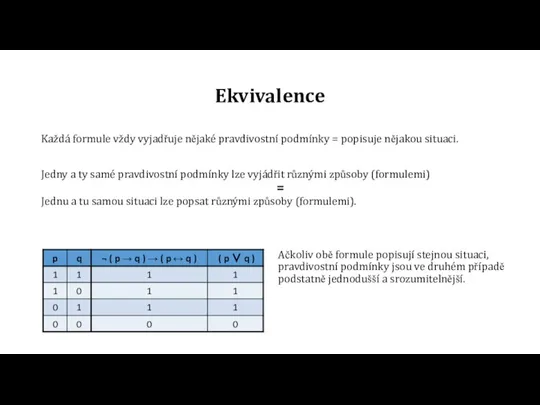
Jednu a tu samou situaci lze popsat různými způsoby (formulemi).
Ačkoliv obě formule popisují stejnou situaci, pravdivostní podmínky jsou ve druhém případě podstatně jednodušší a srozumitelnější.

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=
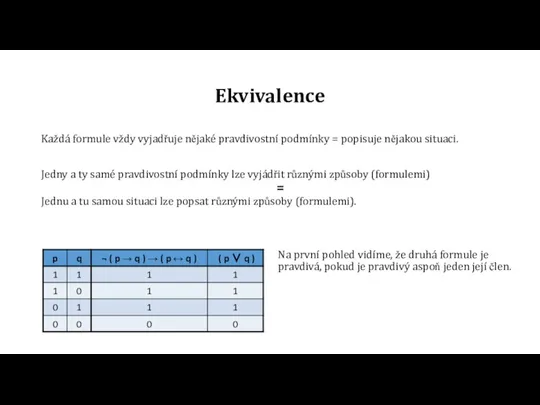
Jednu a tu samou situaci lze popsat různými způsoby (formulemi).
Na první pohled vidíme, že druhá formule je pravdivá, pokud je pravdivý aspoň jeden její člen.

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=
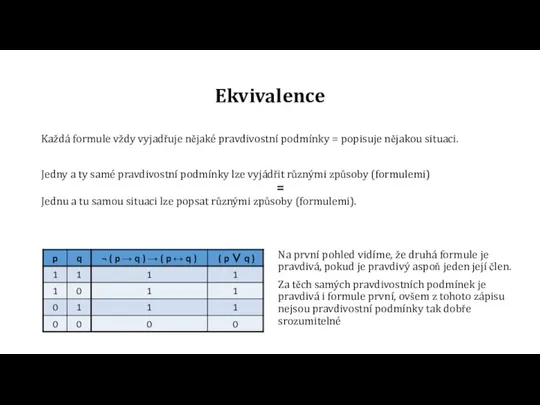
Jednu a tu samou situaci lze popsat různými způsoby (formulemi).
Na první pohled vidíme, že druhá formule je pravdivá, pokud je pravdivý aspoň jeden její člen.
Za těch samých pravdivostních podmínek je pravdivá i formule první, ovšem z tohoto zápisu nejsou pravdivostní podmínky tak dobře srozumitelné

Transformace
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.

Transformace
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými = různě složitými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými = různě složitými způsoby (formulemi).

Transformace
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými = různě složitými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými = různě složitými způsoby (formulemi).
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).

Transformace
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými = různě složitými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými = různě složitými způsoby (formulemi).
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Tedy, vrátíme-li se k předchozímu příkladu, nahradit

Transformace
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými = různě složitými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými = různě složitými způsoby (formulemi).
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Tedy, vrátíme-li se k předchozímu příkladu, nahradit
formuli ¬ ( p → q ) → ( p ↔ q )

Transformace
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými = různě složitými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými = různě složitými způsoby (formulemi).
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Tedy, vrátíme-li se k předchozímu příkladu, přepsat
formuli ¬ ( p → q ) → ( p ↔ q )
na formuli ( p ∨ q )

Transformace
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými = různě složitými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými = různě složitými způsoby (formulemi).
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).
Tento převod (přepis) probíhá tak, že jednotlivé části formule, které vyjadřují nějaké pravdivostní podmínky, nahrazujeme jinými zápisy, které mají stejné pravdivostní podmínky.

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).
Tento převod (přepis) probíhá tak, že jednotlivé části formule, které vyjadřují nějaké pravdivostní podmínky, nahrazujeme jinými zápisy, které mají stejné pravdivostní podmínky.

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).
Tento převod (přepis) probíhá tak, že jednotlivé části formule, které vyjadřují nějaké pravdivostní podmínky, nahrazujeme jinými zápisy, které mají stejné pravdivostní podmínky.
Už jsme si ukázali, že u konjunkce nezáleží na pořadí členů.

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).
Tento převod (přepis) probíhá tak, že jednotlivé části formule, které vyjadřují nějaké pravdivostní podmínky, nahrazujeme jinými zápisy, které mají stejné pravdivostní podmínky.
Už jsme si ukázali, že u konjunkce nezáleží na pořadí členů.
Obě formule jsou ekvivalentní.

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).
Tento převod (přepis) probíhá tak, že jednotlivé části formule, které vyjadřují nějaké pravdivostní podmínky, nahrazujeme jinými zápisy, které mají stejné pravdivostní podmínky.
Už jsme si ukázali, že u konjunkce nezáleží na pořadí členů.
Obě formule jsou ekvivalentní.
změna pořadí členů konjunkce nemá vliv na pravd. podmínky

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).
Tento převod (přepis) probíhá tak, že jednotlivé části formule, které vyjadřují nějaké pravdivostní podmínky, nahrazujeme jinými zápisy, které mají stejné pravdivostní podmínky.
Už jsme si ukázali, že u konjunkce nezáleží na pořadí členů.
Obě formule jsou ekvivalentní.
změna pořadí členů konjunkce nemá vliv na pravd. podmínky
jedná se o ekvivalentní úpravu

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).
Tento převod (přepis) probíhá tak, že jednotlivé části formule, které vyjadřují nějaké pravdivostní podmínky, nahrazujeme jinými zápisy, které mají stejné pravdivostní podmínky.
Už jsme si ukázali, že u konjunkce nezáleží na pořadí členů.
Obě formule jsou ekvivalentní.
změna pořadí členů konjunkce nemá vliv na pravd. podmínky
jedná se o ekvivalentní úpravu
To znamená, že jednu můžeme nahradit tou druhou a naopak.

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).
Tento převod (přepis) probíhá tak, že jednotlivé části formule, které vyjadřují nějaké pravdivostní podmínky, nahrazujeme jinými zápisy, které mají stejné pravdivostní podmínky.
To znamená, že jednu můžeme nahradit tou druhou a naopak.

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).
Tento převod (přepis) probíhá tak, že jednotlivé části formule, které vyjadřují nějaké pravdivostní podmínky, nahrazujeme jinými zápisy, které mají stejné pravdivostní podmínky.
To znamená, že jednu můžeme nahradit tou druhou a naopak.
formuli ( p ∧ q ) → r

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).
Tento převod (přepis) probíhá tak, že jednotlivé části formule, které vyjadřují nějaké pravdivostní podmínky, nahrazujeme jinými zápisy, které mají stejné pravdivostní podmínky.
To znamená, že jednu můžeme nahradit tou druhou a naopak.
formuli ( p ∧ q ) → r
můžeme přepsat na formuli ( q ∧ p ) → r

Transformace
Účelem transformací je přepsat formuli, která vyjadřuje nějaké pravdivostní podmínky do tvaru (zápisu), ze kterého budou tyto pravdivostní podmínky zřejmější (čitelnější, srozumitelnější).
Jedná se tedy o převod (přepis) do jednoduššího tvaru (zápisu).
Tento převod (přepis) probíhá tak, že jednotlivé části formule, které vyjadřují nějaké pravdivostní podmínky, nahrazujeme jinými zápisy, které mají stejné pravdivostní podmínky.
To znamená, že jednu můžeme nahradit tou druhou a naopak.
formuli ( p ∧ q ) → r
můžeme přepsat na formuli ( q ∧ p ) → r
… a na pravdivostních podmínkách to nic nemění

Ekvivalence
Každá formule vždy vyjadřuje nějaké pravdivostní podmínky = popisuje nějakou situaci.
Jedny a ty samé pravdivostní podmínky lze vyjádřit různými způsoby (formulemi)
=
Jednu a tu samou situaci lze popsat různými způsoby (formulemi).
Už jsme si ukázali, že u implikace záleží na pořadí členů, takže implikace „tam“ není ekvivalentní s implikací „zpátky“.

Transformace
A teď už pojďme řešit konkrétní úlohu…

( p ↔ q ) → ( ( ¬ q → p ) → r )
Toto je formule, kterou máme transformovat.

( p ↔ q ) → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek

( p ↔ q ) → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Asi se shodneme na tom, že spojka konjunkce (…a…) a spojka disjunkce (…nebo…) jsou jednodušší a srozumitelnější, než spojky implikace (jestliže…pak…) a ekvivalence (… právě tehdy, když …).

( p ↔ q ) → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Asi se shodneme na tom, že spojka konjunkce (…a…) a spojka disjunkce (…nebo…) jsou jednodušší a srozumitelnější, než spojky implikace (jestliže…pak…) a ekvivalence (… právě tehdy, když …).
Proto se v prvním kroku obě tyto spojky převádějí na konjunkci a disjunkci.

( p ↔ q ) → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
Už jsme si ukázali, že spojku ekvivalence můžeme vyjádřit následujícím zápisy:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)

( p ↔ q ) → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
Už jsme si ukázali, že spojku ekvivalence můžeme vyjádřit následujícím zápisy:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Jedná se o převedení spojky ekvivalence na jiné logické = definice.
Výše jsme si ukázali, proč oba zápisy říkají to samé.

( p ↔ q ) → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
Už jsme si ukázali, že spojku ekvivalence můžeme vyjádřit následujícím zápisy:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Jedná se o převedení spojky ekvivalence na jiné logické = definice.
Výše jsme si ukázali, proč oba zápisy říkají to samé.
Všude, kde se vyskytuje spojka ekvivalence, můžeme ji nahradit jedním z těchto dvou zápisů.

( p ↔ q ) → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
Už jsme si ukázali, že spojku ekvivalence můžeme vyjádřit následujícím zápisy:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Jedná se o převedení spojky ekvivalence na jiné logické = definice.
Výše jsme si ukázali, proč oba zápisy říkají to samé.
Všude, kde se vyskytuje spojka ekvivalence, můžeme ji nahradit jedním z těchto dvou zápisů
Doporučuji ten první. Později se vrátím k tomu proč.

( p ↔ q ) → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
Toto je tedy zákon, podle kterého budeme nahrazovat ekvivalenci.
p ↔ q ( p → q ) ∧ ( q → p )

( p ↔ q ) → ( ( ¬ q → p ) → r )
( p → q ) ∧ ( q → p ) → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
Toto je tedy zákon, podle kterého budeme nahrazovat ekvivalenci.
p ↔ q ( p → q ) ∧ ( q → p )
Protože původní výraz p ↔ q tvořil jeden celek,

( p ↔ q ) → ( ( ¬ q → p ) → r )
( p → q ) ∧ ( q → p ) → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
Toto je tedy zákon, podle kterého budeme nahrazovat ekvivalenci.
p ↔ q ( p → q ) ∧ ( q → p )
Protože původní výraz p ↔ q tvořil jeden celek, musí jeden celek tvořit i nový zápis
( p → q ) ∧ ( q → p ),

( p ↔ q ) → ( ( ¬ q → p ) → r )
( p → q ) ∧ ( q → p ) → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
Toto je tedy zákon, podle kterého budeme nahrazovat ekvivalenci.
p ↔ q ( p → q ) ∧ ( q → p )
Protože původní výraz p ↔ q tvořil jeden celek, musí jeden celek tvořit i nový zápis
( p → q ) ∧ ( q → p ), proto jej musím ohraničit závorkami.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
Toto je tedy zákon, podle kterého budeme nahrazovat ekvivalenci.
p ↔ q ( p → q ) ∧ ( q → p )
Protože původní výraz p ↔ q tvořil jeden celek, musí jeden celek tvořit i nový zápis
( p → q ) ∧ ( q → p ), proto jej musím ohraničit závorkami.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
Nyní budeme nahrazovat implikaci.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q
Implikace je nepravdivá v jediném případě a sice, pokud je přední člen pravdivý a zadní nepravdivý

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q
Implikace je nepravdivá v jediném případě a sice, pokud je přední člen pravdivý a zadní nepravdivý
1 → 0

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q
Implikace je nepravdivá v jediném případě a sice, pokud je přední člen pravdivý a zadní nepravdivý
1 → 0
Tuto situaci popisuje formule p ∧ ¬ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q
Implikace je nepravdivá v jediném případě a sice, pokud je přední člen pravdivý a zadní nepravdivý
1 → 0
Tuto situaci popisuje formule p ∧ ¬ q
(p platí a q neplatí)

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q
Implikace je nepravdivá v jediném případě a sice, pokud je přední člen pravdivý a zadní nepravdivý
1 → 0
Tuto situaci popisuje formule p ∧ ¬ q
(p platí a q neplatí)
Implikace tedy platí, pokud tato situace nenastane.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q
Implikace je nepravdivá v jediném případě a sice, pokud je přední člen pravdivý a zadní nepravdivý
1 → 0
Tuto situaci popisuje formule p ∧ ¬ q
(p platí a q neplatí)
Implikace tedy platí, pokud tato situace nenastane, což popisuje formule ¬ ( p ∧ ¬ q )

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q
Implikace je nepravdivá v jediném případě a sice, pokud je přední člen pravdivý a zadní nepravdivý
1 → 0
Tuto situaci popisuje formule p ∧ ¬ q
(p platí a q neplatí)
Implikace tedy platí, pokud tato situace nenastane, což popisuje formule ¬ ( p ∧ ¬ q )
(nemůže se stát, aby p platilo a q neplatilo)

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q ¬ ( p ∧ ¬ q )

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q ¬ ( p ∧ ¬ q )
Situace, kdy je implikace nepravdivá (1 → 0 ), nenastane, pokud je

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q ¬ ( p ∧ ¬ q )
Situace, kdy je implikace nepravdivá (1 → 0 ), nenastane, pokud je
přední člen nepravdivý ( 0 → 1 )
nebo zadní pravdivý ( 0 → 1 ),

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q ¬ ( p ∧ ¬ q )
Situace, kdy je implikace nepravdivá (1 → 0 ), nenastane, pokud je
přední člen nepravdivý ( 0 → 1 )
nebo zadní pravdivý ( 0 → 1 ),
což popisuje formule ¬ p ∨ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q ¬ ( p ∧ ¬ q )
Situace, kdy je implikace nepravdivá (1 → 0 ), nenastane, pokud je
přední člen nepravdivý ( 0 → 1 )
nebo zadní pravdivý ( 0 → 1 ),
což popisuje formule ¬ p ∨ q
neplatí p nebo platí q,

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q ¬ ( p ∧ ¬ q )
¬ p ∨ q
Vidíme tedy, že spojku implikace můžeme nahradit spojkou konjunkce i disjunkce.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q ¬ ( p ∧ ¬ q )
¬ p ∨ q
Vidíme tedy, že spojku implikace můžeme nahradit spojkou konjunkce i disjunkce.
Měli byste vidět, že oba zápisy říkají to samé jako původní implikace

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q ¬ ( p ∧ ¬ q )
¬ p ∨ q
Vidíme tedy, že spojku implikace můžeme nahradit spojkou konjunkce i disjunkce.
Měli byste vidět, že oba zápisy říkají to samé jako původní implikace – přeříkávají jiným způsobem její pravdivostní podmínky.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q ¬ ( p ∧ ¬ q )
¬ p ∨ q
Asi se shodneme, že druhý zápis je
„hezčí“ = jednodušší.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q ¬ ( p ∧ ¬ q )
¬ p ∨ q
Asi se shodneme, že druhý zápis je
„hezčí“ = jednodušší.
Můžete si jej zapamatovat jako jednoduchý postup – místo implikace se napíše disjunkce a zneguje se přední člen.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( (¬ ¬ q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( (¬ ¬ q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( (¬ ¬ q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( (¬ ¬ q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Před tím ale malá poznámka:
Všimněme si kombinace dvou negací v poslední závorce.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( (¬ ¬ q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Před tím ale malá poznámka:
Všimněme si kombinace dvou negací v poslední závorce.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( (¬ ¬ q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Před tím ale malá poznámka:
Všimněme si kombinace dvou negací v poslední závorce.
Platí, že dvě negace se ruší ¬ ¬ p je to samé jako p

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( (¬ ¬ q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Před tím ale malá poznámka:
Všimněme si kombinace dvou negací v poslední závorce.
Platí, že dvě negace se ruší ¬ ¬ p je to samé jako p
Lze to ukázat v tabulce

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( (¬ ¬ q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Před tím ale malá poznámka:
Všimněme si kombinace dvou negací v poslední závorce.
Platí, že dvě negace se ruší ¬ ¬ p je to samé jako p
Lze to ukázat v tabulce

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( (¬ ¬ q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Před tím ale malá poznámka:
Všimněme si kombinace dvou negací v poslední závorce.
Platí, že dvě negace se ruší ¬ ¬ p je to samé jako p
Lze to ukázat v tabulce
Vidíme, že první a poslední sloupec jsou stejné

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( (¬ ¬ q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Před tím ale malá poznámka:
Všimněme si kombinace dvou negací v poslední závorce.
Platí, že dvě negace se ruší ¬ ¬ p je to samé jako p
Lze to ukázat v tabulce
Vidíme, že první a poslední sloupec jsou stejné
p a ¬¬p jsou ekvivalentní

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( (¬ ¬ q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Před tím ale malá poznámka:
Všimněme si kombinace dvou negací v poslední závorce.
Platí, že dvě negace se ruší ¬ ¬ p je to samé jako p
Lze to ukázat v tabulce
Vidíme, že první a poslední sloupec jsou stejné
p a ¬¬p jsou ekvivalentní
dvojí negaci můžeme zrušit

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( (¬ ¬ q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Před tím ale malá poznámka:
Všimněme si kombinace dvou negací v poslední závorce.
Platí, že dvě negace se ruší ¬ ¬ p je to samé jako p
Lze to ukázat v tabulce
Vidíme, že první a poslední sloupec jsou stejné
p a ¬¬p jsou ekvivalentní
dvojí negaci můžeme zrušit

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Před tím ale malá poznámka:
Všimněme si kombinace dvou negací v poslední závorce.
Platí, že dvě negace se ruší ¬ ¬ p je to samé jako p
Lze to ukázat v tabulce
Vidíme, že první a poslední sloupec jsou stejné
p a ¬¬p jsou ekvivalentní
dvojí negaci můžeme zrušit

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Začněme tou druhou implikací.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Začněme tou druhou implikací.
Princip je stejný – implikaci nahradíme disjunkcí a znegujeme přední člen.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Začněme tou druhou implikací.
Princip je stejný – implikaci nahradíme disjunkcí a znegujeme přední člen.
Předním členem této implikace je ale malá závorka
( q ∨ p )

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Začněme tou druhou implikací.
Princip je stejný – implikaci nahradíme disjunkcí a znegujeme přední člen.
Předním členem této implikace je ale malá závorka
( q ∨ p )

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → (( q ∨ p ) → r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Začněme tou druhou implikací.
Princip je stejný – implikaci nahradíme disjunkcí a znegujeme přední člen.
Předním členem této implikace je ale malá závorka
( q ∨ p )
Tu celou tedy musíme znegovat.
To znamená, že negaci napíšeme PŘED tuto závorku.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ¬ ( q ∨ p ) ∨ r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Začněme tou druhou implikací.
Princip je stejný – implikaci nahradíme disjunkcí a znegujeme přední člen.
Předním členem této implikace je ale malá závorka
( q ∨ p )
Tu celou tedy musíme znegovat.
To znamená, že negaci napíšeme PŘED tuto závorku.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ¬ ( q ∨ p ) ∨ r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Nyní se podíváme na poslední zbývající implikaci.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ¬ ( q ∨ p ) ∨ r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Nyní se podíváme na poslední zbývající implikaci.
Princip je opět stejný – implikaci nahradíme disjunkcí a znegujeme přední člen.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ¬ ( q ∨ p ) ∨ r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Nyní se podíváme na poslední zbývající implikaci.
Princip je opět stejný – implikaci nahradíme disjunkcí a znegujeme přední člen.
Předním členem této implikace je ale malá závorka
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ]

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ¬ ( q ∨ p ) ∨ r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Nyní se podíváme na poslední zbývající implikaci.
Princip je opět stejný – implikaci nahradíme disjunkcí a znegujeme přední člen.
Předním členem této implikace je ale malá závorka
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ]
Tu celou tedy musíme znegovat.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
krok: Odstranění spojek – Definice spojek
Nyní tedy budeme odstraňovat implikace podle tohoto zákona:
p → q ¬ p ∨ q
Máme odstraněny implikace spojující dvě výrokové proměnné (implikace v malých závorkách).
Zbývají nám implikace mezi závorkami.
Nyní se podíváme na poslední zbývající implikaci.
Princip je opět stejný – implikaci nahradíme disjunkcí a znegujeme přední člen.
Předním členem této implikace je ale malá závorka
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ]
Tu celou tedy musíme znegovat.
To znamená, že negaci napíšeme PŘED tuto závorku.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
krok: Odstranění spojek – Definice spojek
Tímto jsme dokončili první krok transformací

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
krok: Odstranění spojek – Definice spojek
Tímto jsme dokončili první krok transformací, a sice odstranění „složitých“ logických spojek implikace a ekvivalence a jejich nahrazení „jednoduchými“ spojkami konjunkce a disjunkce.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
krok: Odstranění spojek – Definice spojek
Tímto jsme dokončili první krok transformací, a sice odstranění „složitých“ logických spojek implikace a ekvivalence a jejich nahrazení „jednoduchými“ spojkami konjunkce a disjunkce.
Zákony, které se v této etapě používají, jsou definice spojek

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
krok: Odstranění spojek – Definice spojek
Tímto jsme dokončili první krok transformací, a sice odstranění „složitých“ logických spojek implikace a ekvivalence a jejich nahrazení „jednoduchými“ spojkami konjunkce a disjunkce.
Zákony, které se v této etapě používají, jsou definice spojek – předpisy, jak pravdivostní podmínky jedné spojky vyjádřit pomocí spojky jiné.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
krok: Odstranění spojek – Definice spojek
Tímto jsme dokončili první krok transformací, a sice odstranění „složitých“ logických spojek implikace a ekvivalence a jejich nahrazení „jednoduchými“ spojkami konjunkce a disjunkce.
Zákony, které se v této etapě používají, jsou definice spojek – předpisy, jak pravdivostní podmínky jedné spojky vyjádřit pomocí spojky jiné.
Ekvivalence:
p ↔ q ( p → q ) ∧ ( q → p )
( p ∧ q ) ∨ ( ¬ p ∧ ¬ q)
Implikace:
p → q ¬ ( p ∧ ¬ q )
¬ p ∨ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte věty:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte věty:
Není pravda, že neprší a nesněží.
Neprší nebo nesněží.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte věty:
Není pravda, že neprší a nesněží.
Neprší nebo nesněží.
Která je srozumitelnější?

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte věty:
Není pravda, že neprší a nesněží.
Neprší nebo nesněží.
Která je srozumitelnější?
Obecně platí, že čím kratší je negovaný úsek, tím je sdělení srozumitelnější.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte věty:
Není pravda, že neprší a nesněží.
Neprší nebo nesněží.
Která je srozumitelnější?
Obecně platí, že čím kratší je negovaný úsek, tím je sdělení srozumitelnější.
V první větě je negovaný složený výraz (souvětí),
ve druhé větě jsou negovány jednoduché věty.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte věty:
Není pravda, že neprší a nesněží.
Neprší nebo nesněží.
Která je srozumitelnější?
Obecně platí, že čím kratší je negovaný úsek, tím je sdělení srozumitelnější.
V první větě je negovaný složený výraz (souvětí),
ve druhé větě jsou negovány jednoduché věty.
Druhá věta je obvykle srozumitelnější.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte věty:
Není pravda, že neprší a nesněží.
Neprší nebo nesněží.
Která je srozumitelnější?
Obecně platí, že čím kratší je negovaný úsek, tím je sdělení srozumitelnější.
V první větě je negovaný složený výraz (souvětí),
ve druhé větě jsou negovány jednoduché věty.
Druhá věta je obvykle srozumitelnější.
De Morganovy zákony umožňují převést negaci složeného výrazu k jeho částem (na negaci jednoduchých tvrzení)

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Konjunkce:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Konjunkce:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Konjunkce:
je pravdivá, pokud jsou pravdivé oba její členy.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Konjunkce:
je pravdivá, pokud jsou pravdivé oba její členy.
je nepravdivá, je-li nepravdivý aspoň jeden její člen

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Konjunkce:
je pravdivá, pokud jsou pravdivé oba její členy.
je nepravdivá, je-li nepravdivý aspoň jeden její člen
=

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Konjunkce:
je pravdivá, pokud jsou pravdivé oba její členy.
je nepravdivá, je-li nepravdivý aspoň jeden její člen
=
je nepravdivé p nebo je nepravdivé q.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Konjunkce:
je pravdivá, pokud jsou pravdivé oba její členy.
je nepravdivá, je-li nepravdivý aspoň jeden její člen
=
je nepravdivé p nebo je nepravdivé q.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Konjunkce:
je pravdivá, pokud jsou pravdivé oba její členy.
je nepravdivá, je-li nepravdivý aspoň jeden její člen
=
je nepravdivé p nebo je nepravdivé q.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Konjunkce:
je pravdivá, pokud jsou pravdivé oba její členy.
je nepravdivá, je-li nepravdivý aspoň jeden její člen
=
je nepravdivé p nebo je nepravdivé q.
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Konjunkce:
je pravdivá, pokud jsou pravdivé oba její členy.
je nepravdivá, je-li nepravdivý aspoň jeden její člen
=
je nepravdivé p nebo je nepravdivé q.
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
Konjunkce je nepravdivá, pokud je nepravdivé p nebo je nepravdivé q.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Analogicky i pro disjunkci

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Disjunkce:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Disjunkce:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Disjunkce:
je pravdivá, pokud je pravdivý alespoň jeden její člen

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Disjunkce:
je pravdivá, pokud je pravdivý alespoň jeden její člen
je nepravdivá, jsou-li nepravdivé oba její členy

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Disjunkce:
je pravdivá, pokud je pravdivý alespoň jeden její člen
je nepravdivá, jsou-li nepravdivé oba její členy
=

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Disjunkce:
je pravdivá, pokud je pravdivý alespoň jeden její člen
je nepravdivá, jsou-li nepravdivé oba její členy
=
je nepravdivé p i q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Disjunkce:
je pravdivá, pokud je pravdivý alespoň jeden její člen
je nepravdivá, jsou-li nepravdivé oba její členy
=
je nepravdivé p i q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Disjunkce:
je pravdivá, pokud je pravdivý alespoň jeden její člen
je nepravdivá, jsou-li nepravdivé oba její členy
=
je nepravdivé p i q
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Disjunkce:
je pravdivá, pokud je pravdivý alespoň jeden její člen
je nepravdivá, jsou-li nepravdivé oba její členy
=
je nepravdivé p i q
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
Disjunkce je nepravdivá, pokud je nepravdivé p i q.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
V rámci transformací je používáme k odstranění negace před složeným výrazem (závorkou).

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
V rámci transformací je používáme k odstranění negace před složeným výrazem (závorkou).
Všimněte si v obou zápisech, že negace mění vše, co se nachází uvnitř závorky

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
V rámci transformací je používáme k odstranění negace před složeným výrazem (závorkou).
Všimněte si v obou zápisech, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ (¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
V rámci transformací je používáme k odstranění negace před složeným výrazem (závorkou).
Všimněte si v obou zápisech, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Věnujme se nyní poslední negované závorce.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
V rámci transformací je používáme k odstranění negace před složeným výrazem (závorkou).
Všimněte si v obou zápisech, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Věnujme se nyní poslední negované závorce.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
V rámci transformací je používáme k odstranění negace před složeným výrazem (závorkou).
Všimněte si v obou zápisech, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Věnujme se nyní poslední negované závorce.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
V rámci transformací je používáme k odstranění negace před složeným výrazem (závorkou).
Všimněte si v obou zápisech, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Věnujme se nyní poslední negované závorce.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.
Jedná se o negaci celé hranaté závorky

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.
Jedná se o negaci celé hranaté závorky

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.
Jedná se o negaci celé hranaté závorky
I v tomto případě platí, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.
Jedná se o negaci celé hranaté závorky.
I v tomto případě platí, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Členy této [ hranaté ] závorky jsou ale závorky ( kulaté ).

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.
Jedná se o negaci celé hranaté závorky.
I v tomto případě platí, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Členy této [ hranaté ] závorky jsou ale závorky ( kulaté ).
… a tou jsou ty členy, které musí být znegovány

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.
Jedná se o negaci celé hranaté závorky.
I v tomto případě platí, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Členy této [ hranaté ] závorky jsou ale závorky ( kulaté ).
… a tou jsou ty členy, které musí být znegovány

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.
Jedná se o negaci celé hranaté závorky.
I v tomto případě platí, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Členy této [ hranaté ] závorky jsou ale závorky ( kulaté ).
… a tou jsou ty členy, které musí být znegovány
Nyní znegujeme obě vnitřní závorky stejně jako v předchozím případě.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.
Jedná se o negaci celé hranaté závorky.
I v tomto případě platí, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Členy této [ hranaté ] závorky jsou ale závorky ( kulaté ).
… a tou jsou ty členy, které musí být znegovány
Nyní znegujeme obě vnitřní závorky stejně jako v předchozím případě.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ (¬ ¬ p ∧ ¬ q ) ∨ (¬ ¬ q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.
Jedná se o negaci celé hranaté závorky.
I v tomto případě platí, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Členy této [ hranaté ] závorky jsou ale závorky ( kulaté ).
… a tou jsou ty členy, které musí být znegovány
Nyní znegujeme obě vnitřní závorky stejně jako v předchozím případě.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ (¬ ¬ p ∧ ¬ q ) ∨ (¬ ¬ q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.
Jedná se o negaci celé hranaté závorky.
I v tomto případě platí, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Členy této [ hranaté ] závorky jsou ale závorky ( kulaté ).
… a tou jsou ty členy, které musí být znegovány
Nyní znegujeme obě vnitřní závorky stejně jako v předchozím případě.
Nyní pouze zrušíme dvojí negace tak, jak jsme si již výše ukázali.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.
Jedná se o negaci celé hranaté závorky.
I v tomto případě platí, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Členy této [ hranaté ] závorky jsou ale závorky ( kulaté ).
… a tou jsou ty členy, které musí být znegovány
Nyní znegujeme obě vnitřní závorky stejně jako v předchozím případě.
Nyní pouze zrušíme dvojí negace tak, jak jsme si již výše ukázali.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Věnujme se nyní negaci na úplném začátku formule.
Jedná se o negaci celé hranaté závorky.
I v tomto případě platí, že negace mění vše, co se nachází uvnitř závorky
zneguje oba členy
a změní spojku
Členy této [ hranaté ] závorky jsou ale závorky ( kulaté ).
… a tou jsou ty členy, které musí být znegovány
Nyní znegujeme obě vnitřní závorky stejně jako v předchozím případě.
Nyní pouze zrušíme dvojí negace tak, jak jsme si již výše ukázali.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejme nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.
Všimněte si, že stále platí, že negace změnila vše, uvnitř závorky na opak:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.
Všimněte si, že stále platí, že negace změnila vše, uvnitř závorky na opak:
¬ p -----> p

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.
Všimněte si, že stále platí, že negace změnila vše, uvnitř závorky na opak:
¬ p -----> p
∨ -----> ∧

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.
Všimněte si, že stále platí, že negace změnila vše, uvnitř závorky na opak:
¬ p -----> p
∨ -----> ∧
q -----> ¬ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.
Všimněte si, že stále platí, že negace změnila vše, uvnitř závorky na opak:
¬ p -----> p
∨ -----> ∧
q -----> ¬ q
∧ -----> ∨

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.
Všimněte si, že stále platí, že negace změnila vše, uvnitř závorky na opak:
¬ p -----> p
∨ -----> ∧
q -----> ¬ q
∧ -----> ∨
¬ q -----> q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.
Všimněte si, že stále platí, že negace změnila vše, uvnitř závorky na opak:
¬ p -----> p
∨ -----> ∧
q -----> ¬ q
∧ -----> ∨
¬ q -----> q
∨ -----> ∧

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.
Všimněte si, že stále platí, že negace změnila vše, uvnitř závorky na opak:
¬ p -----> p
∨ -----> ∧
q -----> ¬ q
∧ -----> ∨
¬ q -----> q
∨ -----> ∧
p -----> ¬ p

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.
Všimněte si, že stále platí, že negace změnila vše, uvnitř závorky naopak.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ¬ (¬ p ∨ q ) ∨ ¬ (¬ q ∨ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.
Všimněte si, že stále platí, že negace změnila vše, uvnitř závorky na opak:
Pokud si troufnete, můžete celou úpravu provést najednou.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
Porovnejte nyní řádky, kdy jsme začali a skončili s úpravou [ hranaté ] závorky.
Všimněte si, že stále platí, že negace změnila vše, uvnitř závorky na opak:
Pokud si troufnete, můžete celou úpravu provést najednou.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony používáme k odstranění negace před složeným výrazem (závorkou).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony používáme k odstranění negace před složeným výrazem (závorkou).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony používáme k odstranění negace před složeným výrazem (závorkou).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).
Jedná se tedy vlastně o definici konjunkce disjunkcí a disjunkce konjunkcí.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony používáme k odstranění negace před složeným výrazem (závorkou).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).
Jedná se tedy vlastně o definici konjunkce disjunkcí a disjunkce konjunkcí.
( p ∨ q ) ¬ ( ¬ p ∧ ¬ q )
( p ∧ q ) ¬ ( ¬ p ∨ ¬ q )

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony používáme k odstranění negace před složeným výrazem (závorkou).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).
Jedná se tedy vlastně o definici konjunkce disjunkcí a disjunkce konjunkcí.
( p ∨ q ) ¬ ( ¬ p ∧ ¬ q )
Disjunkce: Nemůže se stát, aby oba členy, p i q, byly nepravdivé.
( p ∧ q ) ¬ ( ¬ p ∨ ¬ q )
Konjunkce: Nemůže se stát, aby některý z členů, p nebo q, byl nepravdivý.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
2. krok: Odstranění negací - DeMorganovy zákony
De Morganovy zákony používáme k odstranění negace před složeným výrazem (závorkou).
¬ ( p ∨ q ) ( ¬ p ∧ ¬ q )
¬ ( p ∧ q ) ( ¬ p ∨ ¬ q )
De Morganovy zákony vyjadřují vztah mezi konjunkcí a disjunkcí (prostřednictvím negace).
Jedná se tedy vlastně o definici konjunkce disjunkcí a disjunkce konjunkcí.
( p ∨ q ) ¬ ( ¬ p ∧ ¬ q )
( p ∧ q ) ¬ ( ¬ p ∨ ¬ q )
Poznámka:
Stejně jako jsme uměli nahradit implikaci a ekvivalenci konjunkcí a disjunkcí, umíme i konjunkci s disjunkcí v případě potřeby nahradit tou druhou spojkou.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme tyto dva výrazy:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme tyto dva výrazy:
[ ( p ∧ q ) ∨ r ] [ p ∧ ( q ∨ r ) ]

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme tyto dva výrazy:
[ ( p ∧ q ) ∨ r ] [ p ∧ ( q ∨ r ) ]
Jaké jsou jejich pravdivostní podmínky?

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme tyto dva výrazy:
[ ( p ∧ q ) ∨ r ] [ p ∧ ( q ∨ r ) ]
Jaké jsou jejich pravdivostní podmínky?
Není těžké si uvědomit, že se liší.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme tyto dva výrazy:
Jaké jsou jejich pravdivostní podmínky?
Není těžké si uvědomit, že se liší.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme naopak tyto dva výrazy:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme naopak tyto dva výrazy:
[ ( p ∧ q ) ∧ r ] [ p ∧ ( q ∧ r ) ]

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme naopak tyto dva výrazy:
[ ( p ∧ q ) ∧ r ] [ p ∧ ( q ∧ r ) ]
Jaké jsou jejich pravdivostní podmínky?

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme naopak tyto dva výrazy:
[ ( p ∧ q ) ∧ r ] [ p ∧ ( q ∧ r ) ]
Jaké jsou jejich pravdivostní podmínky?
Není těžké si uvědomit, že aby bylo dané tvrzení
pravdivé, musí být pravdivé všechny 3 členy.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme naopak tyto dva výrazy:
[ ( p ∧ q ) ∧ r ] [ p ∧ ( q ∧ r ) ]
Jaké jsou jejich pravdivostní podmínky?
Není těžké si uvědomit, že aby bylo dané tvrzení
pravdivé, musí být pravdivé všechny 3 členy.
Závorky nemají v tomto případě na pravdivostní
podmínky vliv.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme naopak tyto dva výrazy:
[ ( p ∧ q ) ∧ r ] [ p ∧ ( q ∧ r ) ]
Jaké jsou jejich pravdivostní podmínky?
Není těžké si uvědomit, že aby bylo dané tvrzení
pravdivé, musí být pravdivé všechny 3 členy.
Závorky nemají v tomto případě na pravdivostní
podmínky vliv.
Této vlastnosti, kdy pravdivostní podmínky nezáleží na uzávorkování, se říká asociativita.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme naopak tyto dva výrazy:
[ ( p ∧ q ) ∧ r ] [ p ∧ ( q ∧ r ) ]
Jaké jsou jejich pravdivostní podmínky?
Není těžké si uvědomit, že aby bylo dané tvrzení
pravdivé, musí být pravdivé všechny 3 členy.
Závorky nemají v tomto případě na pravdivostní
podmínky vliv.
Této vlastnosti, kdy pravdivostní podmínky nezáleží na uzávorkování, se říká asociativita.
Používá se k odstraňování nadbytečných závorek.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme naopak tyto dva výrazy:
[ ( p ∧ q ) ∧ r ] [ p ∧ ( q ∧ r ) ]
Jaké jsou jejich pravdivostní podmínky?
Není těžké si uvědomit, že aby bylo dané tvrzení
pravdivé, musí být pravdivé všechny 3 členy.
Závorky nemají v tomto případě na pravdivostní
podmínky vliv.
Této vlastnosti, kdy pravdivostní podmínky nezáleží na uzávorkování, se říká asociativita.
Používá se k odstraňování nadbytečných závorek.
Vnitřní závorky jsou v tomto případě zbytečné.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
U správně utvořených formulí záleží na závorkách.
Ke každé spojce patří závorka, aby bylo zřejmé,
které dva členy spojuje.
Porovnejme naopak tyto dva výrazy:
[ ( p ∧ q ) ∧ r ] [ p ∧ ( q ∧ r ) ]
Jaké jsou jejich pravdivostní podmínky?
Není těžké si uvědomit, že aby bylo dané tvrzení
pravdivé, musí být pravdivé všechny 3 členy.
Závorky nemají v tomto případě na pravdivostní
podmínky vliv.
Této vlastnosti, kdy pravdivostní podmínky nezáleží na uzávorkování, se říká asociativita.
Používá se k odstraňování nadbytečných závorek.
Vnitřní závorky jsou v tomto případě zbyteční, stačí psát
( p ∧ q ∧ r )

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
Je vlastnost konjunkce, kdy nezáleží na uzávorkování.
Několikanásobná konjunkce bude pravdivá pouze tehdy, budou-li pravdivé všechny její členy, bez ohledu na to, jak jsou spojené dohromady.
Stačí tedy psát pouze vnější závorku
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
Tu samou vlastnost má pochopitelně i disjunkce
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Několikanásobná disjunkce bude pravdivá pouze tehdy, bude-li pravdivý alespoň jeden její člen, bez ohledu na to, jak jsou spojené dohromady.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Vraťme se k naší formuli.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Vraťme se k naší formuli.
První kulatá závorka není nadbytečná, protože uvnitř je konjunkce a vně disjunkce.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Vraťme se k naší formuli.
První kulatá závorka není nadbytečná, protože uvnitř je konjunkce a vně disjunkce.
Druhá kulatá závorka je na tom úplně stejně – uvnitř je konjunkce a vně disjunkce – tudíž není nadbytečná.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Vraťme se k naší formuli.
První kulatá závorka není nadbytečná, protože uvnitř je konjunkce a vně disjunkce.
Druhá kulatá závorka je na tom úplně stejně – uvnitř je konjunkce a vně disjunkce – tudíž není nadbytečná.
Rovněž třetí kulatá vnitřní závorka není nadbytečná, protože uvnitř a vně jsou opět různé spojky.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Vraťme se k naší formuli.
Naopak u hranaté závorky na začátku formule se ukazuje, že nadbytečné je – uvnitř i vně této závorky je disjunkce.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Vraťme se k naší formuli.
Naopak u hranaté závorky na začátku formule se ukazuje, že nadbytečné je – uvnitř i vně této závorky je disjunkce.
Tuto závorku tedy můžeme odstranit.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Vraťme se k naší formuli.
Naopak u hranaté závorky na začátku formule se ukazuje, že nadbytečné je – uvnitř i vně této závorky je disjunkce.
Tuto závorku tedy můžeme odstranit.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Vraťme se k naší formuli.
Naopak u hranaté závorky na začátku formule se ukazuje, že nadbytečné je – uvnitř i vně této závorky je disjunkce.
Tuto závorku tedy můžeme odstranit.
Stejně tak je tomu i s vnější závorkou v zadní části formule.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( (¬ q ∧ ¬ p ) ∨ r )
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Vraťme se k naší formuli.
Naopak u hranaté závorky na začátku formule se ukazuje, že nadbytečné je – uvnitř i vně této závorky je disjunkce.
Tuto závorku tedy můžeme odstranit.
Stejně tak je tomu i s vnější závorkou v zadní části formule.
I tuto závorky tedy můžeme odstranit.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Vraťme se k naší formuli.
Naopak u hranaté závorky na začátku formule se ukazuje, že nadbytečné je – uvnitř i vně této závorky je disjunkce.
Tuto závorku tedy můžeme odstranit.
Stejně tak je tomu i s vnější závorkou v zadní části formule.
I tuto závorky tedy můžeme odstranit.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Vraťme se k naší formuli.
Naopak u hranaté závorky na začátku formule se ukazuje, že nadbytečné je – uvnitř i vně této závorky je disjunkce.
Tuto závorku tedy můžeme odstranit.
Stejně tak je tomu i s vnější závorkou v zadní části formule.
I tuto závorky tedy můžeme odstranit.
Vidíme, že odstranění nadbytečných závorek nám zjednodušuje a zpřehledňuje zápis formule.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Distributivita:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Distributivita:
Distributivní zákony se používají k odstraňování vnitřních závorek, které nadbytečné nejsou.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Distributivita:
Distributivní zákony se používají k odstraňování vnitřních závorek, které nadbytečné nejsou.
V naší formuli ale taková situace nenastala.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Distributivita:
Distributivní zákony se používají k odstraňování vnitřních závorek, které nadbytečné nejsou.
V naší formuli ale taková situace nenastala.
Výklad tedy odložíme na později.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
3. krok: Odstranění závorek – asociativita, distributivita
Asociativita:
je vlastnost konjunkce, kdy nezáleží na uzávorkování.
[ ( p ∧ q ) ∧ r ] ( p ∧ q ∧ r )
[ ( p ∨ q ) ∨ r ] ( p ∨ q ∨ r )
Používá se k odstraňování nadbytečných závorek, kdy uvnitř a vně závorky je stejná spojka.
Distributivita:
[ p ∧ ( q ∨ r ) ] [ ( p ∧ q ) ∨ (p ∧ r ) ]
[ p ∨ ( q ∧ r ) ] [ ( p ∨ q ) ∧ ( p ∨ r ) ]
[ ( p ∧ q ) ∨ ( r ∧ s ) ]
[ ( p ∨ r ) ∧ (p ∨ s ) ∧ ( q ∨ r ) ∧ ( q ∨ s ) ]
[ ( p ∨ q ) ∧ ( r ∨ s ) ]
[ ( p ∧ r ) ∨ (p ∧ s ) ∨ ( q ∧ r ) ∨ ( q ∧ s ) ]

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
4. krok: Zjednodušení
Nyní vidíme, že již máme poměrně jednoduchý zápis.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
4. krok: Zjednodušení
Nyní vidíme, že již máme poměrně jednoduchý zápis.
Naše formule je disjunkcí o čtyřech členech – 3 závorky a jedna proměnná.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
4. krok: Zjednodušení
Nyní vidíme, že již máme poměrně jednoduchý zápis.
Naše formule je disjunkcí o čtyřech členech – 3 závorky a jedna proměnná.
Z tohoto zápisu už jsou pravdivostní podmínky původní formule zřetelnější:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
4. krok: Zjednodušení
Nyní vidíme, že již máme poměrně jednoduchý zápis.
Naše formule je disjunkcí o čtyřech členech – 3 závorky a jedna proměnná.
Z tohoto zápisu už jsou pravdivostní podmínky původní formule zřetelnější:
Daná formule bude mít výslednou pravdivostní hodnotu 1 při ohodnoceních, kde:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
4. krok: Zjednodušení
Nyní vidíme, že již máme poměrně jednoduchý zápis.
Naše formule je disjunkcí o čtyřech členech – 3 závorky a jedna proměnná.
Z tohoto zápisu už jsou pravdivostní podmínky původní formule zřetelnější:
Daná formule bude mít výslednou pravdivostní hodnotu 1 při ohodnoceních, kde:
p má hodnotu 1 a q má hodnotu 0 (1. závorka)
nebo
p má hodnotu 0 a q má hodnotu 1 (2. závorka)
nebo
p i q mají hodnotu 0 (3. závorka)
nebo
r má hodnotu 1 (poslední člen)

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
4. krok: Zjednodušení
Nyní vidíme, že již máme poměrně jednoduchý zápis.
Naše formule je disjunkcí o čtyřech členech – 3 závorky a jedna proměnná.
Z tohoto zápisu už jsou pravdivostní podmínky původní formule zřetelnější:
Daná formule bude mít výslednou pravdivostní hodnotu 1 při ohodnoceních, kde:
p má hodnotu 1 a q má hodnotu 0 (1. závorka)
nebo
p má hodnotu 0 a q má hodnotu 1 (2. závorka)
nebo
p i q mají hodnotu 0 (3. závorka)
nebo
r má hodnotu 1 (poslední člen)
Každá závorka tak představuje jednu podmínku, která musí být splněna.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
4. krok: Zjednodušení
Nyní vidíme, že již máme poměrně jednoduchý zápis.
Naše formule je disjunkcí o čtyřech členech – 3 závorky a jedna proměnná.
Z tohoto zápisu už jsou pravdivostní podmínky původní formule zřetelnější:
Daná formule bude mít výslednou pravdivostní hodnotu 1 při ohodnoceních, kde:
p má hodnotu 1 a q má hodnotu 0 (1. závorka)
nebo
p má hodnotu 0 a q má hodnotu 1 (2. závorka)
nebo
p i q mají hodnotu 0 (3. závorka)
nebo
r má hodnotu 1 (poslední člen)
Každá závorka tak představuje jednu podmínku, která musí být splněna.
Tento zápis ale ještě může být dále zjednodušen.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ (¬ q ∧ ¬ p ) ∨ r
4. krok: Zjednodušení
Nejprve přeuspořádáme členy v jednotlivých závorkách podle abecedy, aby se nám závorky snadno porovnávaly.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
4. krok: Zjednodušení
Nejprve přeuspořádáme členy v jednotlivých závorkách podle abecedy, aby se nám závorky snadno porovnávaly.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
4. krok: Zjednodušení
Nejprve přeuspořádáme členy v jednotlivých závorkách podle abecedy, aby se nám závorky snadno porovnávaly.
Nyní na první pohled vidíme, že první tři závorky mají stejé členy, liší ase ale rozložením negací.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
Toto je zjednodušovací zákon, který můžeme použít v situaci, kdy se nám dvě závorky liší pouze o jednu negaci.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
Toto je zjednodušovací zákon, který můžeme použít v situaci, kdy se nám dvě závorky liší pouze o jednu negaci.
Říká, že dvě takové závorky lze nahradit tím výrazem, který je v obou závorkách stejný; člen, který se liší o negaci zmizí.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
Toto je zjednodušovací zákon, který můžeme použít v situaci, kdy se nám dvě závorky liší pouze o jednu negaci.
Říká, že dvě takové závorky lze nahradit tím výrazem, který je v obou závorkách stejný; člen, který se liší o negaci zmizí.
Všimněte si, že daná formule vlastně říká, že p platí v obou případech, a že q platí nebo neplatí – tedy na jeho hodnotě nezáleží.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
Toto je zjednodušovací zákon, který můžeme použít v situaci, kdy se nám dvě závorky liší pouze o jednu negaci.
Podíváme-li se na první dvě závorky, měli bychom vidět,
že na ně tento zákon použít nemůžeme, protože se liší o negace dvě, nikoliv jen jednu.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
Toto je zjednodušovací zákon, který můžeme použít v situaci, kdy se nám dvě závorky liší pouze o jednu negaci.
Podíváme-li se na první dvě závorky, měli bychom vidět,
že na ně tento zákon použít nemůžeme, protože se liší o negace dvě, nikoliv jen jednu.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
Toto je zjednodušovací zákon, který můžeme použít v situaci, kdy se nám dvě závorky liší pouze o jednu negaci.
Podíváme-li se na první dvě závorky, měli bychom vidět,
že na ně tento zákon použít nemůžeme, protože se liší o negace dvě, nikoliv jen jednu.
Naopak jej můžeme použít na závorku první a třetí.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
Toto je zjednodušovací zákon, který můžeme použít v situaci, kdy se nám dvě závorky liší pouze o jednu negaci.
Podíváme-li se na první dvě závorky, měli bychom vidět,
že na ně tento zákon použít nemůžeme, protože se liší o negace dvě, nikoliv jen jednu.
Naopak jej můžeme použít na závorku první a třetí. Tady je rozdíl skutečně jen o jednu negaci u p; ¬ q je naopak v obou závorkách beze změny.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
Toto je zjednodušovací zákon, který můžeme použít v situaci, kdy se nám dvě závorky liší pouze o jednu negaci.
Podíváme-li se na první dvě závorky, měli bychom vidět,
že na ně tento zákon použít nemůžeme, protože se liší o negace dvě, nikoliv jen jednu.
Naopak jej můžeme použít na závorku první a třetí. Tady je rozdíl skutečně jen o jednu negaci u p; ¬ q je naopak v obou závorkách beze změny.
Uvedený zákon říká, že v tom případě můžeme obě závorky nahradit tím, co je v obou závorkách stejné.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
Toto je zjednodušovací zákon, který můžeme použít v situaci, kdy se nám dvě závorky liší pouze o jednu negaci.
Podíváme-li se na první dvě závorky, měli bychom vidět,
že na ně tento zákon použít nemůžeme, protože se liší o negace dvě, nikoliv jen jednu.
Naopak jej můžeme použít na závorku první a třetí. Tady je rozdíl skutečně jen o jednu negaci u p; ¬ q je naopak v obou závorkách beze změny.
Uvedený zákon říká, že v tom případě můžeme obě závorky nahradit tím, co je v obou závorkách stejné.
To je v tomto případě ¬ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
Další zjednodušovací zákony:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
Toto je další zjednodušovací zákon, který říká, že je-li kratší výraz obsažen v nějakém delším, pak ten delší výraz nemá na výsledné pravdivostní hodnoty vliv, a zůstává jen ten kratší.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
Toto je další zjednodušovací zákon, který říká, že je-li kratší výraz obsažen v nějakém delším, pak ten delší výraz nemá na výsledné pravdivostní hodnoty vliv, a zůstává jen ten kratší.
Můžete si to představit na dvojici:
Prší nebo prší a sněží.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
Toto je další zjednodušovací zákon, který říká, že je-li kratší výraz obsažen v nějakém delším, pak ten delší výraz nemá na výsledné pravdivostní hodnoty vliv, a zůstává jen ten kratší.
Můžete si to představit na dvojici:
Prší nebo prší a sněží.
p ∨ ( p ∧ q )
Situace, kdy prší a sněží zároveň už jsou mezi těmi, kdy prší.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
Toto je další zjednodušovací zákon, který říká, že je-li kratší výraz obsažen v nějakém delším, pak ten delší výraz nemá na výsledné pravdivostní hodnoty vliv, a zůstává jen ten kratší.
Můžete si to představit na dvojici:
Prší nebo prší a sněží.
p ∨ ( p ∧ q )
Situace, kdy prší a sněží zároveň už jsou mezi těmi, kdy prší.
Závorka tedy sice má více členů, nepřidává ale žádné další situace.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
Toto je další zjednodušovací zákon, který říká, že je-li kratší výraz obsažen v nějakém delším, pak ten delší výraz nemá na výsledné pravdivostní hodnoty vliv, a zůstává jen ten kratší.
Můžete si to představit na dvojici:
Prší nebo prší a sněží.
p ∨ ( p ∧ q )
Situace, kdy prší a sněží zároveň už jsou mezi těmi, kdy prší.
Závorka tedy sice má více členů, nepřidává ale žádné další situace. Proto nemá na výsledné pravdivostní podmínky vliv.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
Tento zákon nemůžeme v naší situaci použít, protože q před závorkou a v závorce se liší o negaci.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
Tento zákon nemůžeme v naší situaci použít, protože q před závorkou a v závorce se liší o negaci.
Na takovou situaci lze ale uplatnit poslední ze zjednodušovacích zákonů:

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon se týká situace, kdy se výraz před závorkou a v závorce liší o negaci.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon se týká situace, kdy se výraz před závorkou a v závorce liší o negaci.
V takovém případě zůstává člen před závorkou včetně spojky, a zbytek závorky.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon se týká situace, kdy se výraz před závorkou a v závorce liší o negaci.
V takovém případě zůstává člen před závorkou včetně spojky, a zbytek závorky.
Člen s negací navíc uvnitř závorky zmizí.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Výraz vlastně říká, že platí p, a když neplatí tak platí q.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Výraz vlastně říká, že platí p, a když neplatí tak platí q.
Čili platí p nebo q.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon nyní můžeme použít, protože q před závorkou a v závorce se liší o negaci.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon nyní můžeme použít, protože q před závorkou a v závorce se liší o negaci.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon nyní můžeme použít, protože q před závorkou a v závorce se liší o negaci.
Všimněte si, že nezáleží na tom, zda se negace nachází u člen před závorkou nebo v závorce.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon nyní můžeme použít, protože q před závorkou a v závorce se liší o negaci.
Všimněte si, že nezáleží na tom, zda se negace nachází u člen před závorkou nebo v závorce.
Důležitý je ROZDÍL o negaci mezi oběma členy.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon nyní můžeme použít, protože q před závorkou a v závorce se liší o negaci.
Všimněte si, že nezáleží na tom, zda se negace nachází u člen před závorkou nebo v závorce.
Důležitý je ROZDÍL o negaci mezi oběma členy.
Můžete si to případně představit i takto:
¬ q ∨ ( ¬ p ∧ ¬ ¬ q )

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon nyní můžeme použít, protože q před závorkou a v závorce se liší o negaci.
Všimněte si, že nezáleží na tom, zda se negace nachází u člen před závorkou nebo v závorce.
Důležitý je ROZDÍL o negaci mezi oběma členy.
Můžete si to případně představit i takto:
¬ q ∨ ( ¬ p ∧ ¬ ¬ q )
Před závorkou je ¬ q a v závorce je ¬ q s negací navíc

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon nyní můžeme použít, protože q před závorkou a v závorce se liší o negaci.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon nyní můžeme použít, protože q před závorkou a v závorce se liší o negaci.
Zákon říká, že zůstane člen před závorkou včetně spojky

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon nyní můžeme použít, protože q před závorkou a v závorce se liší o negaci.
Zákon říká, že zůstane člen před závorkou včetně spojky
a zbytek závorky.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Tento zákon nyní můžeme použít, protože q před závorkou a v závorce se liší o negaci.
Zákon říká, že zůstane člen před závorkou včetně spojky
a zbytek závorky.
Ostatní zmizí

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
¬ q ∨ ¬ p ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
¬ q ∨ ¬ p ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Není těžké si uvědomit, že tento zápis už nelze dále zjednodušovat.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
¬ q ∨ ¬ p ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Není těžké si uvědomit, že tento zápis už nelze dále zjednodušovat.
Původní formule má výslednou pravdivostní hodnotu 1
při těch ohodnoceních, kdy

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
¬ q ∨ ¬ p ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Není těžké si uvědomit, že tento zápis už nelze dále zjednodušovat.
Původní formule má výslednou pravdivostní hodnotu 1
při těch ohodnoceních, kdy
p je nepravdivé (má hodnotu 0)
nebo
q je nepravdivé (má hodnotu 0)
nebo
r je pravdivé (má hodnotu 1)

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
¬ q ∨ ¬ p ∨ r
¬ p ∨ ¬ q ∨ r
4. krok: Zjednodušení
Zjednodušovací zákony:
( p ∧ q ) ∨ ( p ∧ ¬ q ) p
( p ∨ q ) ∧ ( p ∨ ¬ q ) p
p ∨ ( p ∧ q ) p
p ∧ ( p ∨ q ) p
p ∨ ( ¬ p ∧ q ) p ∨ q
p ∧ ( ¬ p ∨ q ) p ∧ q
Není těžké si uvědomit, že tento zápis už nelze dále zjednodušovat.
Původní formule má výslednou pravdivostní hodnotu 1
při těch ohodnoceních, kdy
p je nepravdivé (má hodnotu 0)
nebo
q je nepravdivé (má hodnotu 0)
nebo
r je pravdivé (má hodnotu 1)
Pro pořádek můžeme jednotlivé členy ještě srovnat podle abecedy.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
¬ q ∨ ¬ p ∨ r
¬ p ∨ ¬ q ∨ r
4. krok: Zjednodušení
Pro úplnost si ještě ukážeme zjednodušovací zákony, které jsme v této konkrétní transformaci nepotřebovali.

( p ↔ q ) → ( ( ¬ q → p ) → r )
[ ( p → q ) ∧ ( q → p ) ] → ( ( ¬ q → p ) → r )
[ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] → ( ( q ∨ p ) → r )
¬ [ (¬ p ∨ q ) ∧ (¬ q ∨ p ) ] ∨ ( ¬ ( q ∨ p ) ∨ r )
[ ( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ] ∨ ( (¬ q ∧ ¬ p ) ∨ r )
( p ∧ ¬ q ) ∨ ( q ∧ ¬ p ) ∨ ( ¬ q ∧ ¬ p ) ∨ r
( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) ∨ r
¬ q ∨ ( ¬ p ∧ q ) ∨ r
¬ q ∨ ¬ p ∨ r
¬ p ∨ ¬ q ∨ r
4. krok: Zjednodušení
Pro úplnost si ještě ukážeme zjednodušovací zákony, které jsme v této konkrétní transformaci nepotřebovali.
Tyto zákony by se teoreticky nemusely vůbec vykládat, protože se jedná o bezprostřední důsledky pravdivostních podmínek jednotlivých spojek.