Слайд 2МЕТОДЫ ОПТИМАЛЬНОГО
УПРАВЛЕНИЯ
Л-1
Экстремумы функций

Слайд 3Оптимальные Решения
Примеры Классических Задач
Построить прямоугольник максимальной площади с заданным периметром

(частная задача, см. 4.1)
2. (Задача Эвклида) В треугольник вписать параллелограмм максимальной площади
3. В плоскости треугольника найти точку, сумма расстояний от которой до вершин треугольника минимальна
Слайд 4Оптимальные Решения:
Примеры Классических Задач
4.1 (Изопериметрическая задача)
Какую максимальную площадь можно охватить замкнутой

кривой заданной длины ?
4.2 (Задача Дидоны) Дана веревка длины L. Какую максимальную площадь
(у прибрежной зоны- вдоль прямой) можно охватить данной веревкой ?
Слайд 5Оптимальные Решения:
Примеры Классических Задач
5. (З. о Брахистохроне)
Даны точки А и

В на разной высоте. По какой кривой, соединяющей эти точки, шар спустится за минимальное время (под действием только силы тяжести)
Слайд 6Оптимальные Решения:
Примеры Классических Задач
6. (З. об Оптимальном проектировании)
Коробка изготавливается из

листов размера a*b. Для этого из углов вырезают квадраты x*x и сгибают вдоль линий.
Как делать вырезы так, чтоб получить коробку максимального обЪема ?
Слайд 7Задача о перевозках (транспортная задача)
7. Имеется m пунктов производства (поставки) некоторого однородного

продукта и n пунктов его потребления. Для каждого пункта производства i=1,…,m, и каждого пункта его потребления j=1,…,n, заданы:
ai – объем производства в пункте i;
bj – объем потребления в пункте j;
сij – затраты на перевозку 1цы продукта от пункта производства i до пункта потребления j.
(потребление не превышает производства).
Задача: Составить план перевозок:
- не выводящий за пределы производства,
- полностью обеспечивающий всех потребителей,
- дающий минимум суммарных затрат на перевозку
Слайд 8Задача о бродячем торговце
(задача коммивояжера)
8. Имеется n+1 город;
сij – матрица

расстояния между городами (i -j)
Выезжая из исходного города, коммивояжер должен побывать во всех остальных городах ровно 1 раз и вернуться в исходный город.
Составить оптимальный маршрут…
(по времени, стоимости, расстоянию)
Слайд 9Задачи Оптимального Управления
9. (простейшая задача о быстродействии ) (движение управляемой тележки)
Масса тележки

m, в точке x0, скорость- v0. Внешняя сила (тяга) – u, текущая координата – x(t), задаются физические ограничения на тягу. Задача: как за минимальное время, с учетом всех ограничений на управление (скорость, ускорение) достичь точки x0 и остановиться (достичь с нулевой скоростью)
Слайд 10Непрерывные Функции
Дана ф-я f(x),
одномерная ф-я:
многомерная ф-я
x=(x1,…,xn ) ф-ия f(x)=f(x1,…,xn )

в D
Непрерывная ф-я: если при x→x0 lim f(x)=f(x0),
тогда ф-я непрерывна в т. x0
Ф-я f(x) непрерывна в области D, if она непрерывна в каждой точке
Слайд 11Непрерывные Функции
Дана ф-я f(x),
одномерная ф-я:
многомерная ф-я
x=(x1,…,xn ) ф-ия f(x)=f(x1,…,xn )

в D
Непрерывная ф-я: если при x→x0 lim f(x)=f(x0),
тогда ф-я непрерывна в т. x0
Ф-я f(x) непрерывна в области D, if она непрерывна в каждой точке
Слайд 12Непрерывные Функции
D=[a,b] – отрезок, - замкнутое множество (=содержит все свои предельные очки)
![Непрерывные Функции D=[a,b] – отрезок, - замкнутое множество (=содержит все свои предельные](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/947040/slide-11.jpg)
D=(a,b) – интервал.
Свойства:
Th. (Больцано-Коши о промежуточном значении)
Если непрерывная ф-я принимает на отрезке знаечния разных знаков, то найдется точка, в которой ф-я =0.
Th (Вейерштрасса о максим и миним значениях)
Непрерывная на отрезке ф-я ограничена и есть точки, где ф-я принимает максим и миним значения.
Слайд 13Свойства непрерывных функций
Тh. (Вейерштрасса)
Непрерывная ф-я f(x1,…,xn) , заданная на компакте K

, достигает на этом компакте своего максимума и минимума.
Слайд 14Дифференцируемые ф-ии
Дана ф-я f(x),
Ф-я f(x), определенная в D,
называется дифференцируемой в

т. a,
если
При этом:
Слайд 15Дифференцируемые ф-ии
Обозначения:
С(X) – множ-во непрерывных в области X функций,
D(X) – дифференцируемые в

X функции,
частое обозначение f∈Ck(X) :
существует k производных, и k-ая производная непрерывна
Слайд 16Частные производные
Дана ф-я f(x), f(x)=f(x1,…,xn ) в
Частные производные:

Слайд 17Экстремумы
Пусть
Рассмотрим классические методы оптимизации, сводящиеся к нахождению оптимума
ф-ии f(x1,…,xn)

в D.
Дана ф-я Def. Точка x0 назыв т. глобального максимума
(в D), если для всех выполняется нер-во
Слайд 18локальный экстремум
Пусть Def. Точка x0 назыв т. локального максимума
ф-ии f(x) (в

области D),
если существует окрестность т. x0 , U(x0 ), такая, что для всех выполняется нер-во
Примеры (лок и глоб экстремумов)
Слайд 19Базовая теорема
Пусть
Th (Ферма). Если x0 - т. локального экстремума дифференцируемой ф-ии

f(x) в откр. Области D, тогда
Пусть St(f)={x: f’(x)=0} – множ-во стационарных точек.
Тогда: точки экстремума содержатся в множ-ве стационарных точек (обратное не верно).
Пусть D=[a, b] – отрезок на прямой.
f задана на прямой, тогда точки глобального экстремума содержатся в множ-ве критических точек
Слайд 20Базовая теорема
Пусть т.е., f = f(x1,…,xn).
Th (обобщение). Если x0 - т. локального

экстремума дифференцируемой ф-ии f(x1,…,xn), тогда
Здесь:
(опрератор набла)
Слайд 21Глобальный экстремум
Правило. Точки глобального экстремума содержатся в множестве ее критических точек:
где

- граница области D.
Слайд 22Линии уровня
Графический метод нахождения экстремумов на примере n=2.
Линии уровня функции f(x,y):
(min

f≤ c ≤max f)
Через каждую точку плоскости М(x0,y0) (входящую в область определения фу-ии) проходит только одна линия уровня: f(x,y)= f(x0,y0)
1. Графический метод нахожд. экстремумов ф-ий на основе нахождения линий уровня. (рис с.30,31, ВР).
2. Использование градиента функции: Направление градиента совпадает с направлением наибольшей скорости роста фу-и в каждой точке. Он перпендикулярен линии уровня.
Слайд 23Нахождение Экстремумов
Примеры задач
f → opt (max, min)
1. y=f(x) → extr

(sup / max; inf / min )
2. f(x,y) → extr
3. f(x,y)=C → extr (анализ линий уровня)
Слайд 24Условный экстремум
Метод Лагранжа нахождения усл. экстремумов функций в заданной области.
Задача:

Пусть , f = f(x1,…,xn).
f→opt (max/min) при условии, что x=(x1,…,xn) удовлетворяют системе ограничений
(предполагается, что фу-ии f и gi являются
ф-ями класса C1 в области определения










![Непрерывные Функции D=[a,b] – отрезок, - замкнутое множество (=содержит все свои предельные](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/947040/slide-11.jpg)












 Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7
Обработка экспериментальных данных. Многофакторная регрессия. Лекция 7 Знакомство с деятельностью Ивана Грозного, через решение математических задач
Знакомство с деятельностью Ивана Грозного, через решение математических задач Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Решение задач на движение
Решение задач на движение Числовая окружность
Числовая окружность Разряды и классы чисел
Разряды и классы чисел Решение задач на проценты. Концентрация
Решение задач на проценты. Концентрация Стереометрия (геометрия в пространстве)
Стереометрия (геометрия в пространстве) Презентация на тему Третий признак равенства треугольников
Презентация на тему Третий признак равенства треугольников  Логическая задача со спичками
Логическая задача со спичками Квадратный трехчлен. Самостоятельная работа
Квадратный трехчлен. Самостоятельная работа Система уравнений. Метод алгебраического сложения
Система уравнений. Метод алгебраического сложения Простейшие геометрические уравнения
Простейшие геометрические уравнения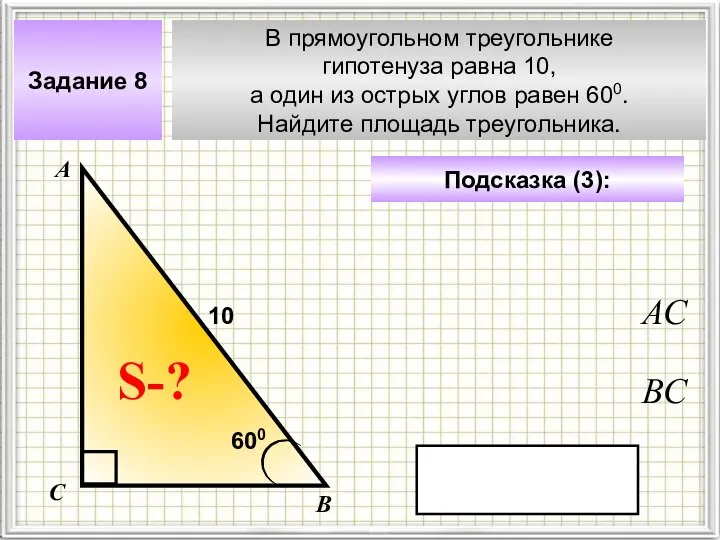 Треугольники (задачи для 9 класса)
Треугольники (задачи для 9 класса) Упражнения
Упражнения Система двух случайных величин. Многомерные СВ
Система двух случайных величин. Многомерные СВ Тригонометрические уравнения
Тригонометрические уравнения Признаки подобия треугольника
Признаки подобия треугольника Число и цифра 5
Число и цифра 5 Естественный отбор и его математические характеристики
Естественный отбор и его математические характеристики Понятие многогранника. Правильные многогранники
Понятие многогранника. Правильные многогранники Усеченый конус
Усеченый конус Свойства медианы треугольника
Свойства медианы треугольника Векторы (повторение). 8 класс
Векторы (повторение). 8 класс Математические структуры
Математические структуры Задачи на движение. Встречное движение
Задачи на движение. Встречное движение Исследование функции при помощи производной
Исследование функции при помощи производной ОГЭ 2020-21. Задание №11. Прямая, гипербола, парабола
ОГЭ 2020-21. Задание №11. Прямая, гипербола, парабола