Содержание
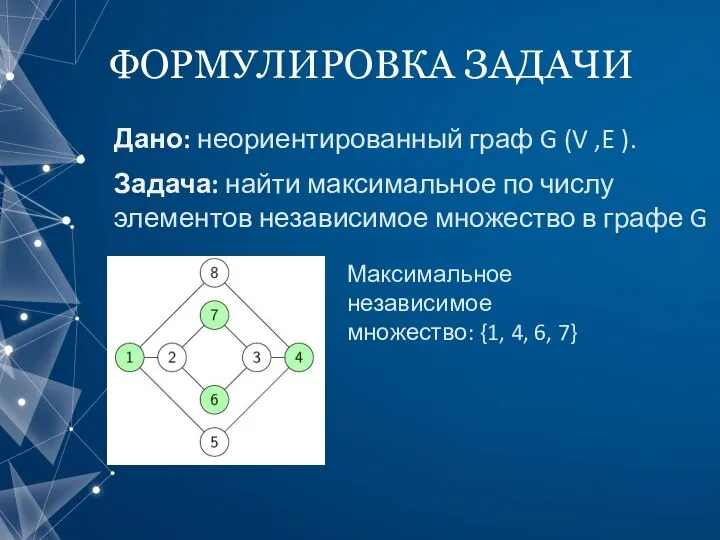
- 2. ФОРМУЛИРОВКА ЗАДАЧИ Дано: неориентированный граф G (V ,E ). Задача: найти максимальное по числу элементов независимое
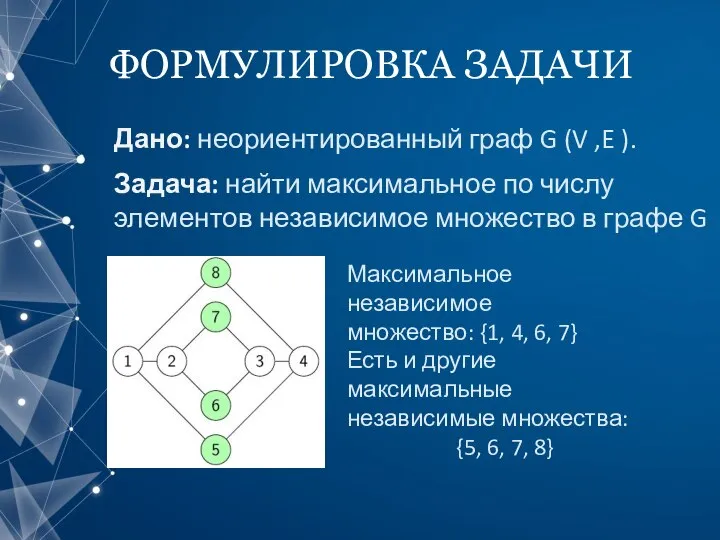
- 3. ФОРМУЛИРОВКА ЗАДАЧИ Дано: неориентированный граф G (V ,E ). Задача: найти максимальное по числу элементов независимое
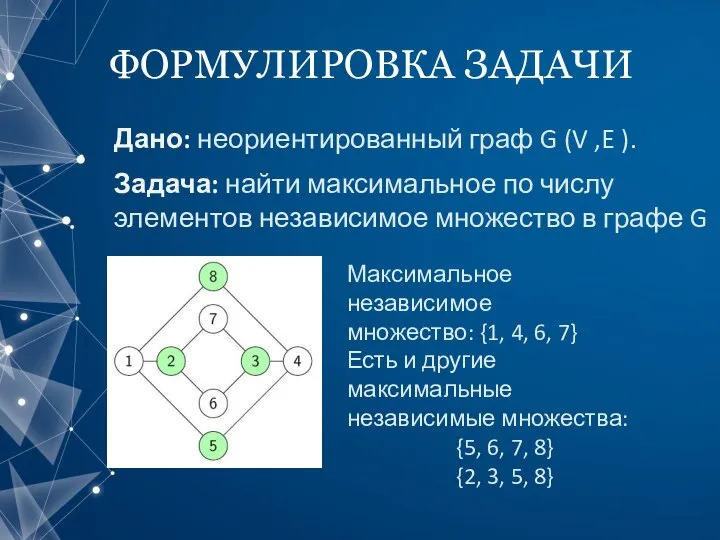
- 4. ФОРМУЛИРОВКА ЗАДАЧИ Дано: неориентированный граф G (V ,E ). Задача: найти максимальное по числу элементов независимое
- 5. МЕТОД ПОЛНОГО ПЕРЕБОРА Алгоритм полного перебора проверяет все подмножества вершин, являются ли они независимыми множествами. Этот
- 6. МЕТОД ПОЛНОГО ПЕРЕБОРА Алгоритм проверяет каждую вершину на независимость с другими вершинами и составляет для нее
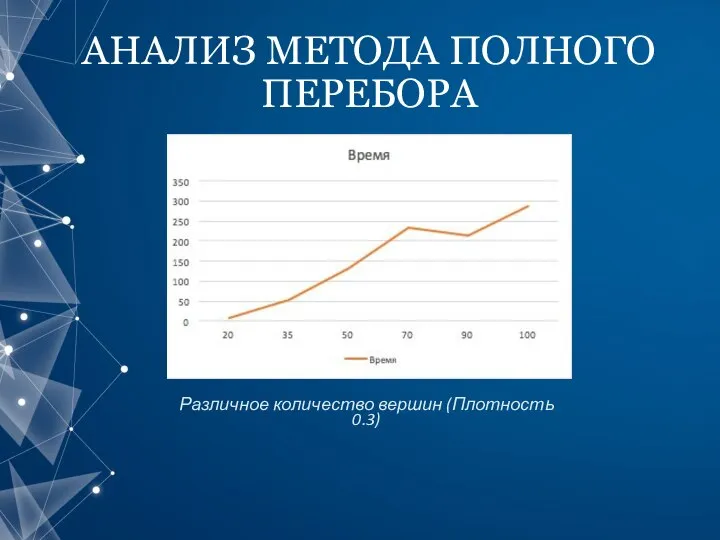
- 7. АНАЛИЗ МЕТОДА ПОЛНОГО ПЕРЕБОРА Различное количество вершин (Плотность 0.3)
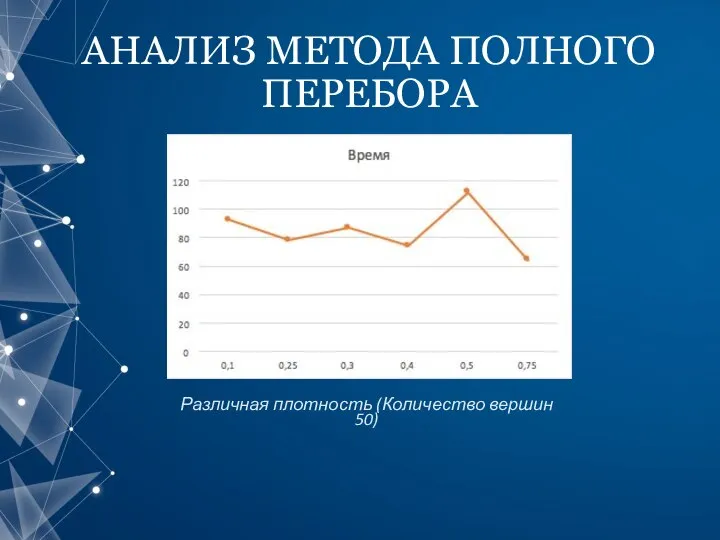
- 8. АНАЛИЗ МЕТОДА ПОЛНОГО ПЕРЕБОРА Различная плотность (Количество вершин 50)
- 9. АЛГОРИТМ БРОНА-КЕРБОША Способом уменьшения количества рассматриваемых вариантов является поиск с возвращением, этот метод лежит в основе
- 10. АЛГОРИТМ БРОНА-КЕРБОША На каждом шаге алгоритма множество V разбито на четыре части: M — текущее независимое
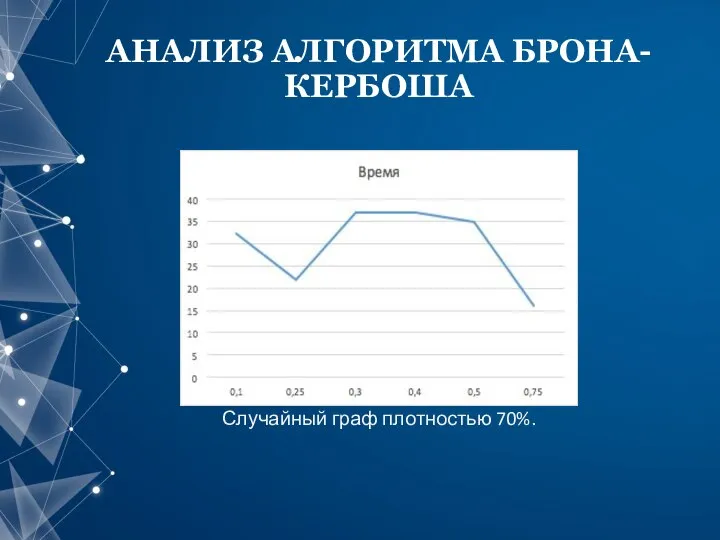
- 11. АНАЛИЗ АЛГОРИТМА БРОНА-КЕРБОША Случайный граф плотностью 70%.
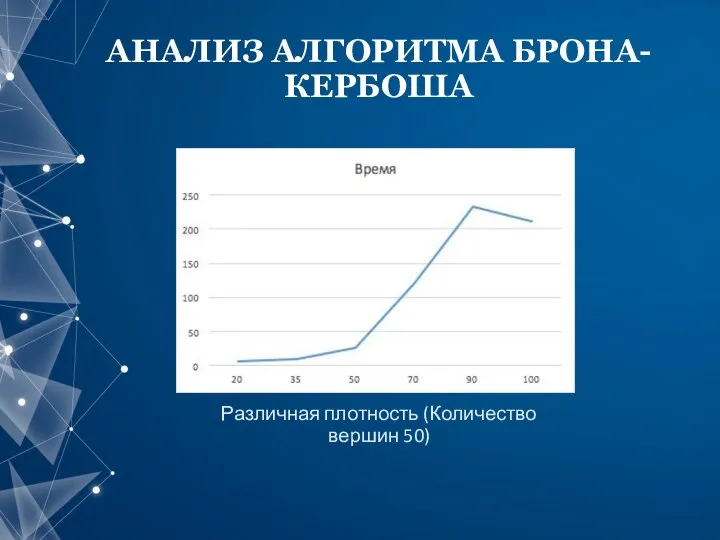
- 12. АНАЛИЗ АЛГОРИТМА БРОНА-КЕРБОША Различная плотность (Количество вершин 50)
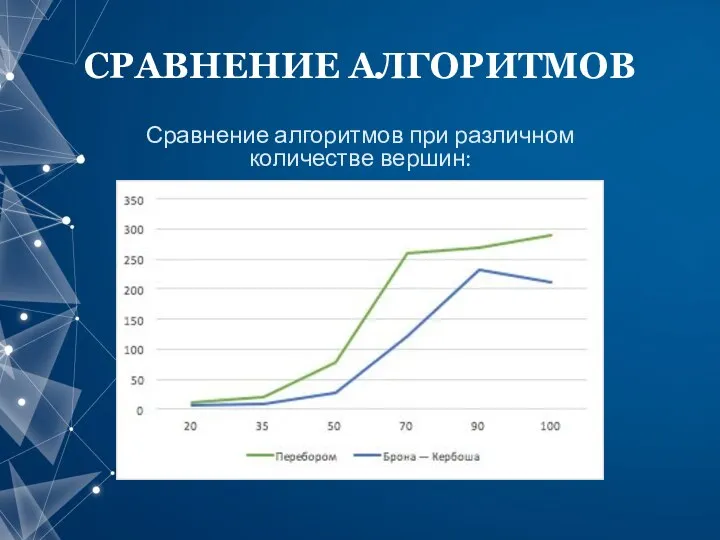
- 13. СРАВНЕНИЕ АЛГОРИТМОВ Сравнение алгоритмов при различном количестве вершин:
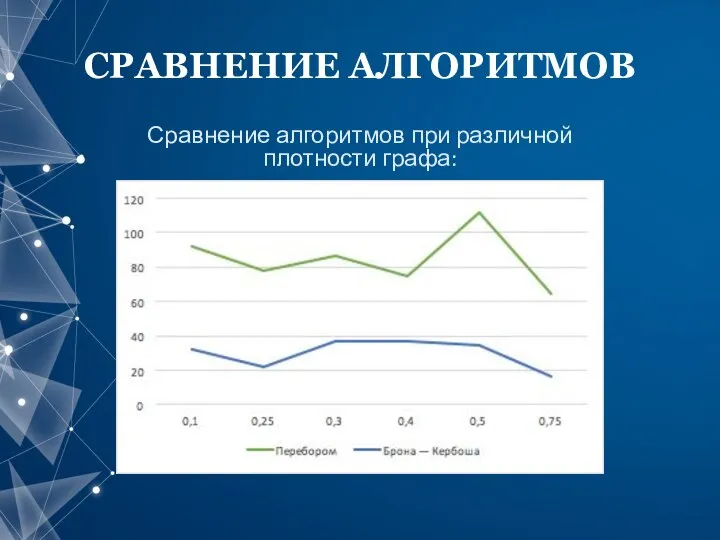
- 14. СРАВНЕНИЕ АЛГОРИТМОВ Сравнение алгоритмов при различной плотности графа:
- 15. ВЫВОД На основании проведенного исследования можно сделать вывод, что алгоритм Брона-Кербоша остается одним из самых эффективных
- 17. Скачать презентацию





 Презентация на тему Геометрическая прогрессия и ее свойство
Презентация на тему Геометрическая прогрессия и ее свойство  Трикутники
Трикутники Перпендикуляр и наклонная к плоскости. Решение задач
Перпендикуляр и наклонная к плоскости. Решение задач Презентация на тему Иррациональные числа (8 класс)
Презентация на тему Иррациональные числа (8 класс)  Тригонометрия. Математическая игра АС-11
Тригонометрия. Математическая игра АС-11 Презентация на тему Сдвиг графика функции y = x вдоль осей координат
Презентация на тему Сдвиг графика функции y = x вдоль осей координат  Отображение. Отражение относительно прямой. Преобразование единичного квадрата
Отображение. Отражение относительно прямой. Преобразование единичного квадрата Решение задач
Решение задач Старинные меры массы и длины
Старинные меры массы и длины Скалярное произведение векторов
Скалярное произведение векторов Волшебный треугольник
Волшебный треугольник Тела вращения
Тела вращения Равнобедренный треугольник
Равнобедренный треугольник Пифагор и литература
Пифагор и литература Решение примеров и простых задач в пределах 10
Решение примеров и простых задач в пределах 10 Заниматика. Миром управляют числа
Заниматика. Миром управляют числа Случайные процессы с дискретными состояниями
Случайные процессы с дискретными состояниями Параллельные прямые
Параллельные прямые Lecture 6. Techniques of Integration (part 1)
Lecture 6. Techniques of Integration (part 1) Аналитическая панель
Аналитическая панель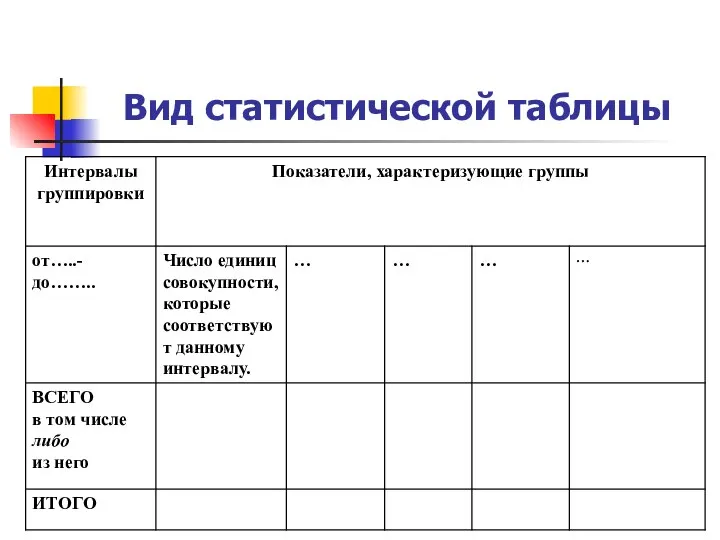 Вид статистической таблицы
Вид статистической таблицы Случаи сложения вида +7
Случаи сложения вида +7 Усеченная пирамида
Усеченная пирамида График равномерного движения
График равномерного движения Задачи на проценты. Схемы
Задачи на проценты. Схемы Многогранники в нашей жизни
Многогранники в нашей жизни Прямоугольный параллелепипед. Урок обобщения и систематизации знаний
Прямоугольный параллелепипед. Урок обобщения и систематизации знаний Презентация на тему Комбинации шара с многогранниками и фигурами вращения
Презентация на тему Комбинации шара с многогранниками и фигурами вращения