Содержание
- 2. В основе регрессионного анализа лежит предположение, что зависимая переменная является функций одной или нескольких независимых переменных.
- 3. Простейшей регрессионной моделью является парная линейная регрессия. Уравнение парной линейной регрессии в общем виде следующее: у=b0+b1x
- 4. Зависимая (результирующая) переменная должна быть непрерывной количественной переменной. Независимая переменная должна быть непрерывной или дихотомической. Категориальные
- 5. Каждое значение зависимой переменной должно быть независимо от других значений. Такие зависимости возникают если опрашивать одного
- 6. Ошибка предсказания для каждого значения не должна зависеть от ошибки предсказания других значений (тест Дарбина-Уотсона), остатки
- 7. Построить уравнение парной линейной регрессии для переменных «Возраст» и «Заболевания зубов» (измеренной по пятибалльной шкале, где
- 8. Теоретически мы должны доказать, что изучение связи между причиной и следствием имеет смысл. Причина всегда по
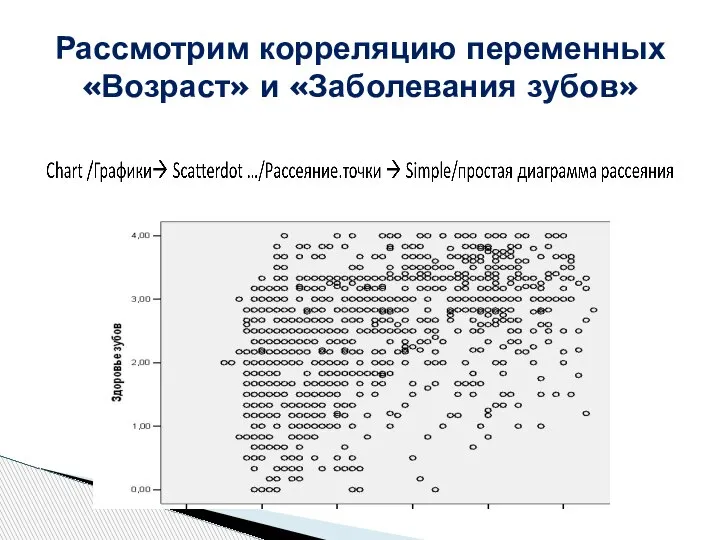
- 9. Рассмотрим корреляцию переменных «Возраст» и «Заболевания зубов»
- 10. Analyze/ Анализ ? Correlation/Корреляции ? Bivariate/Парные Проверка на наличие корреляции возраста и заболевания зубов
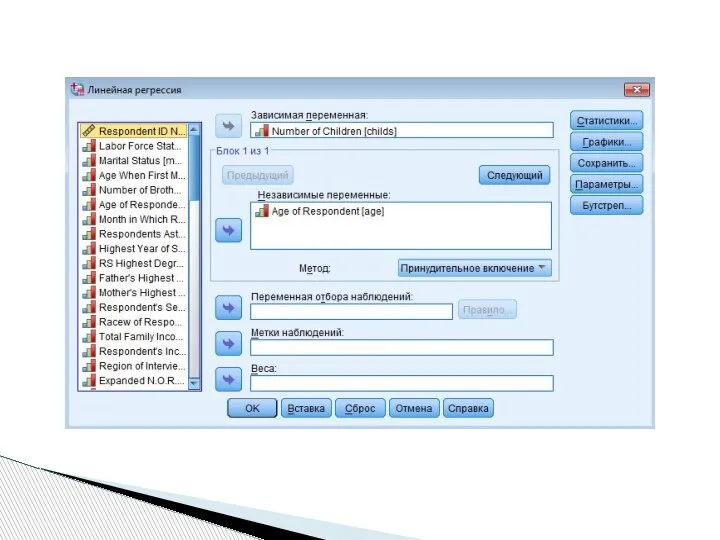
- 11. Выполнение команды: Analyze/Анализ ? Regression/Регрессия ? Linear/Линейная В поле Dependent Имя зависимой переменной В поле Independent(s)
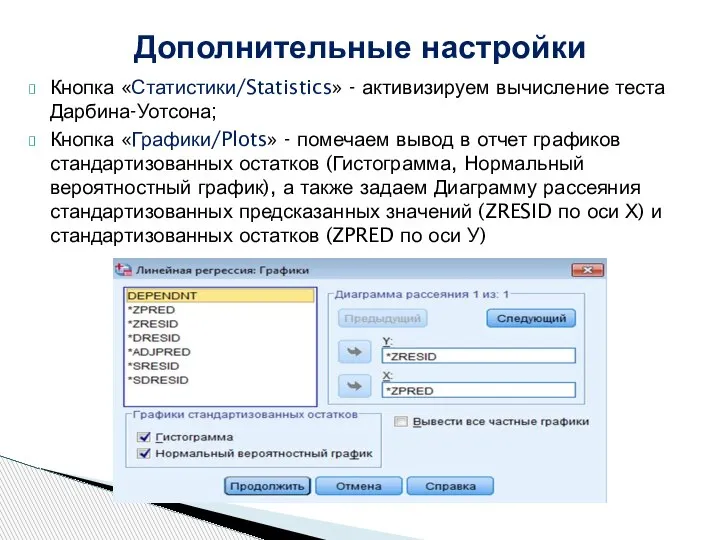
- 13. Кнопка «Статистики/Statistics» - активизируем вычисление теста Дарбина-Уотсона; Кнопка «Графики/Plots» - помечаем вывод в отчет графиков стандартизованных
- 14. у=1,295+0,033x Результаты выполнения команд регрессионного анализа
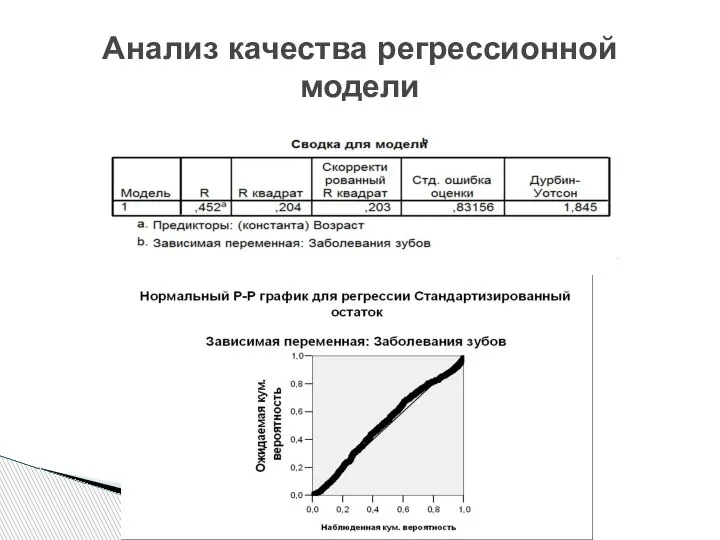
- 15. Анализ качества регрессионной модели
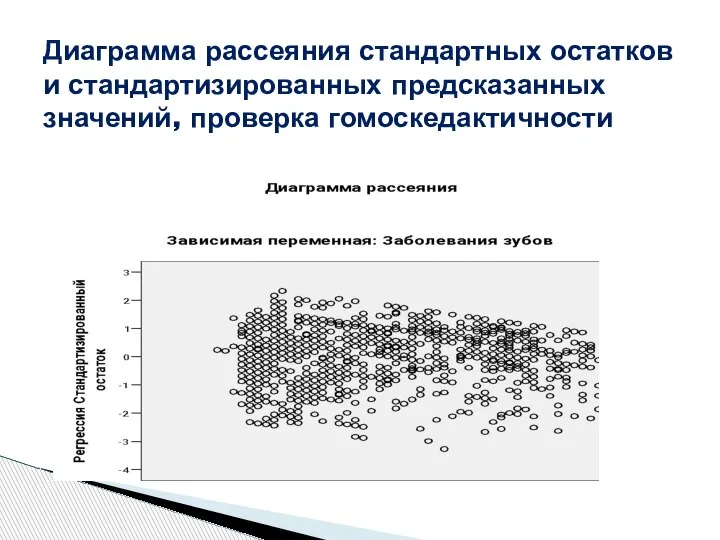
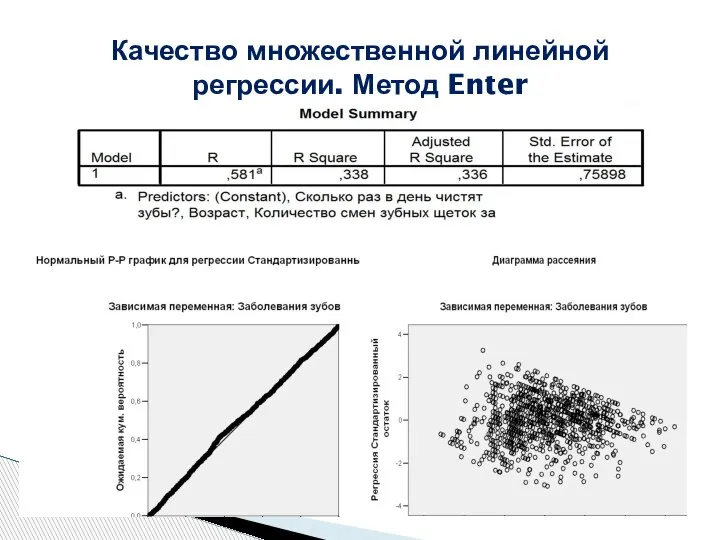
- 16. Диаграмма рассеяния стандартных остатков и стандартизированных предсказанных значений, проверка гомоскедактичности
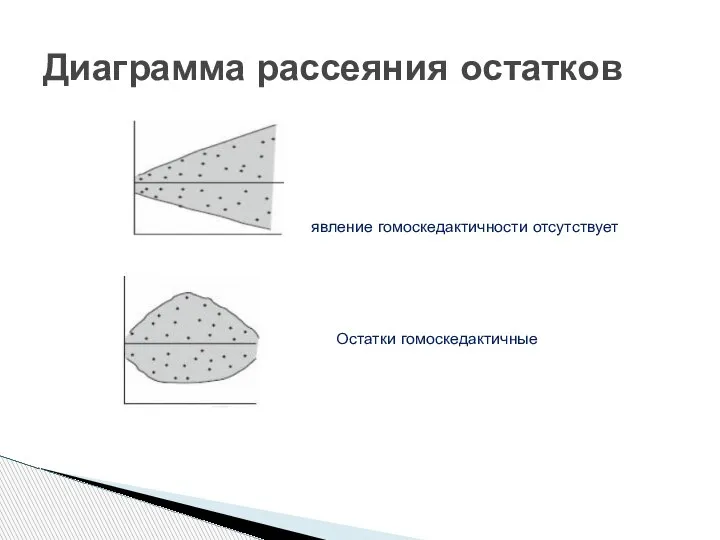
- 17. явление гомоскедактичности отсутствует Остатки гомоскедактичные Диаграмма рассеяния остатков
- 18. Множественная линейная регрессия В большинстве задач следствие не может быть объяснено одной единственной причиной; как правило,
- 19. Построить уравнение множественной линейной регрессии для зависимой переменной «Заболевания зубов» и независимых переменных «Возраст», «Периодичность чистки
- 20. Выполнение команды: Analyze ? Regression ? Linear В поле Dependent Имя зависимой переменной В поле Independent(s)
- 21. В случае множественной регрессии можно использовать установленный по умолчанию метод Enter (включения всех переменных в модель
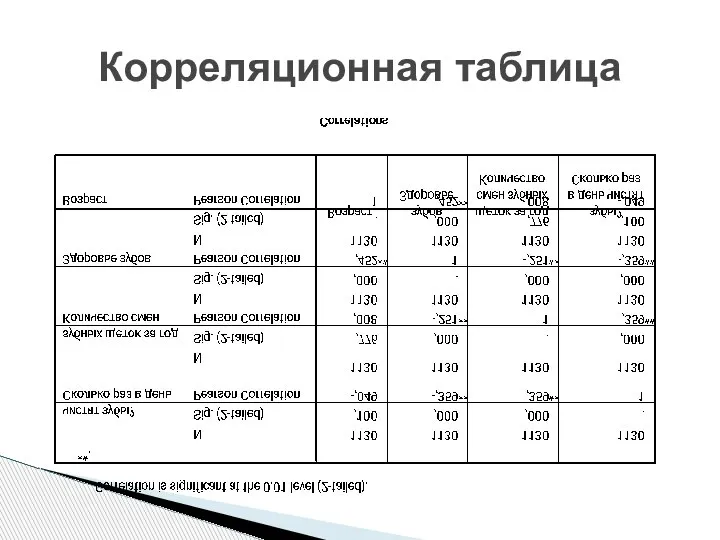
- 22. Корреляционная таблица
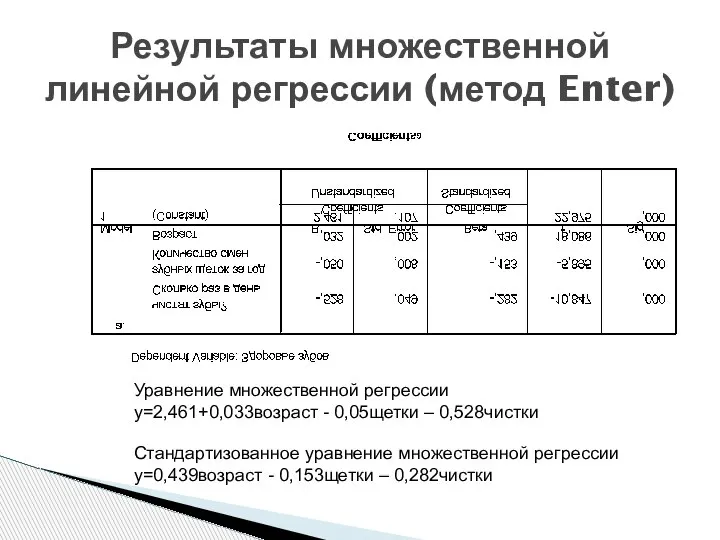
- 23. Результаты множественной линейной регрессии (метод Enter) Уравнение множественной регрессии у=2,461+0,033возраст - 0,05щетки – 0,528чистки Стандартизованное уравнение
- 24. Качество множественной линейной регрессии. Метод Enter
- 25. Результаты множественной линейной регрессии (метод Stepwise)
- 27. Скачать презентацию















 Движение. Тест № 6. 9 класс
Движение. Тест № 6. 9 класс Решение тригонометрических уравнений. Уравнения, сводящиеся к алгебраическим
Решение тригонометрических уравнений. Уравнения, сводящиеся к алгебраическим Движение в математике
Движение в математике Равнобедренный треугольник. Окружность
Равнобедренный треугольник. Окружность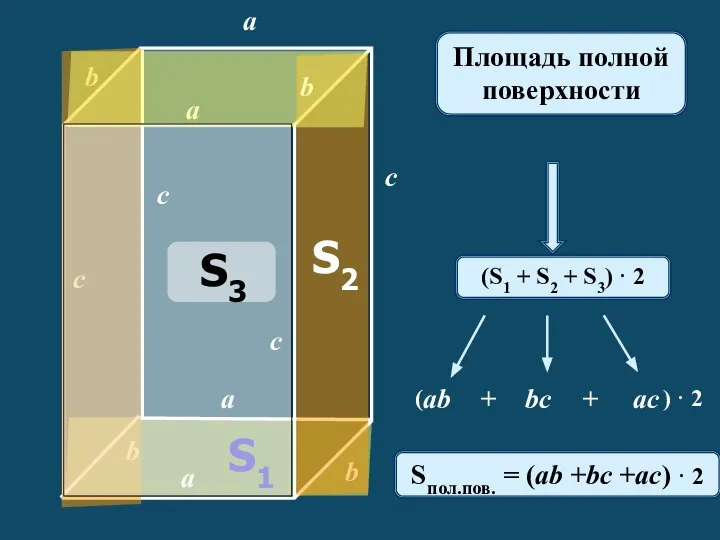 Площадь полной поверхности
Площадь полной поверхности Веселый счет (Счет в прямом и обратном порядке в пределах 10)
Веселый счет (Счет в прямом и обратном порядке в пределах 10) Производная произведения. Производная частного
Производная произведения. Производная частного Единицы измерения объема в истории
Единицы измерения объема в истории Презентация на тему Многоугольники (1 класс)
Презентация на тему Многоугольники (1 класс)  Дифференциальные уравнения (продолжение)
Дифференциальные уравнения (продолжение) Свойства функции
Свойства функции Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ
Устный счет на уроках математики в 9 классе по подготовке к экзаменам в форме ОГЭ Статистический опрос жителей Санкт-Петербурга о применении ими пиротехнических изделий
Статистический опрос жителей Санкт-Петербурга о применении ими пиротехнических изделий Дроби
Дроби Производная в экономике
Производная в экономике Задание 2. Задача минимизировать время сбора утром на работу и в школу семьи из трех человек: отец, сын (10 лет), дочь (6 лет)
Задание 2. Задача минимизировать время сбора утром на работу и в школу семьи из трех человек: отец, сын (10 лет), дочь (6 лет) Комбинаторика. Решение задач
Комбинаторика. Решение задач Презентация по математике "Ломаные числа" -
Презентация по математике "Ломаные числа" -  Построения циркулем и линейкой
Построения циркулем и линейкой Презентация на тему Буквенные выражения (2 класс)
Презентация на тему Буквенные выражения (2 класс)  Понятие Марковского случайного процесса
Понятие Марковского случайного процесса Определение знаков коэффициентов K и b в линейной функции по их графикам
Определение знаков коэффициентов K и b в линейной функции по их графикам Признаки параллелограмма
Признаки параллелограмма Сумма углов треугольника. Решение задач
Сумма углов треугольника. Решение задач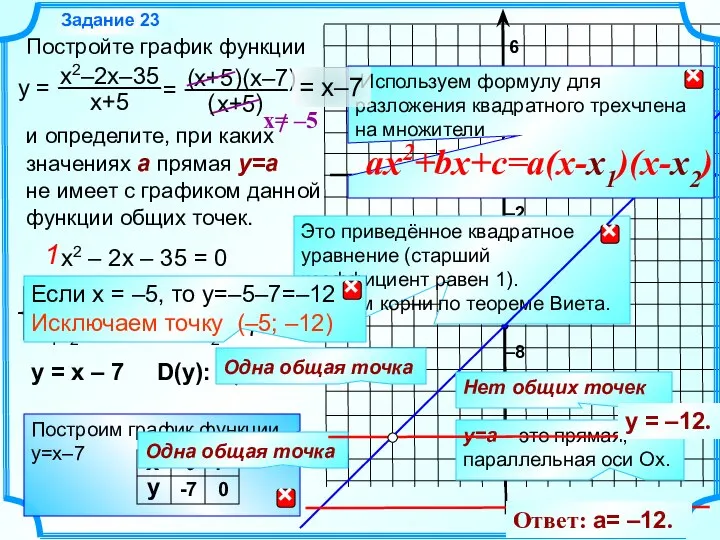 Прямая. Часть II
Прямая. Часть II Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике Понятие логарифма
Понятие логарифма Как математика учит критическому мышлению
Как математика учит критическому мышлению