Содержание
- 2. Изобразим: а) две неравные окружности; б) два неравных квадрата; в) два неравных равнобедренных прямоугольных треугольника; г)
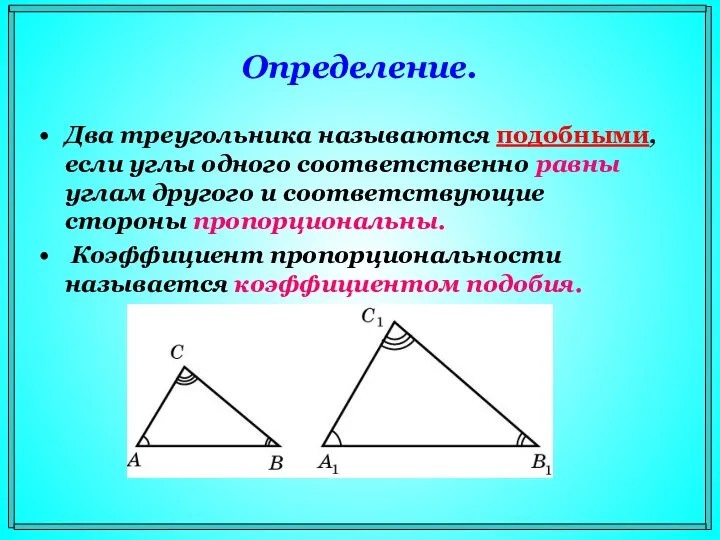
- 3. Определение. Два треугольника называются подобными, если углы одного соответственно равны углам другого и соответствующие стороны пропорциональны.
- 4. Что значит, что Δ АВС подобен треугольнику Δ A1В1С1? Углы равны Стороны пропорциональны Для своих изображенных
- 5. Δ АВС подобен Δ A1В1С1. similitude сходство, подобие Δ АВС ~ Δ A1В1С1
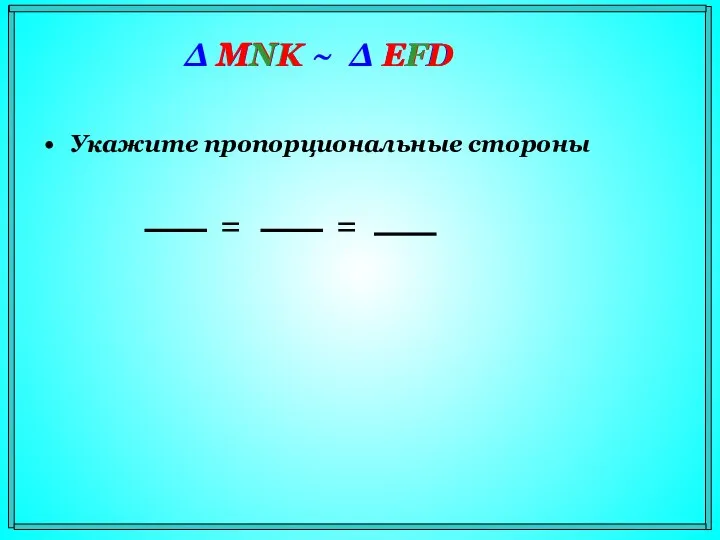
- 6. Укажите пропорциональные стороны Δ MNK ~ Δ EFD MN EF = NK FD = M K
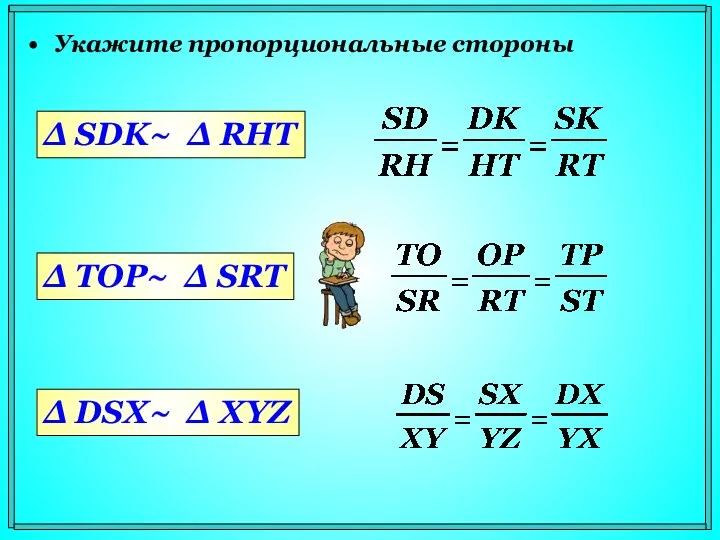
- 7. Укажите пропорциональные стороны Δ SDK~ Δ RHT Δ TOP~ Δ SRT Δ DSX~ Δ XYZ
- 8. Стороны треугольника равны 5 см, 8 см и 10 см. Найдите стороны подобного ему треугольника, если
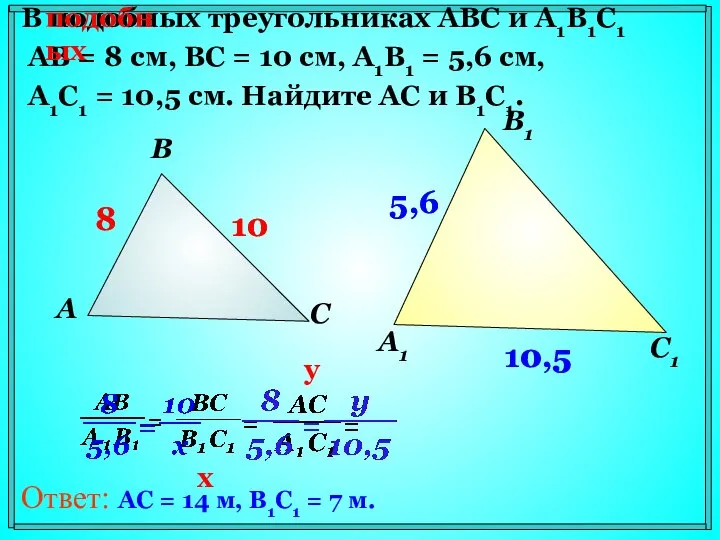
- 9. В подобных треугольниках АВС и А1В1С1 АВ = 8 см, ВС = 10 см, А1В1 =
- 10. Физкультминутка: Долго тянется урок Много вы решали Не поможет тут звонок, Раз глаза устали. Занимаемся все
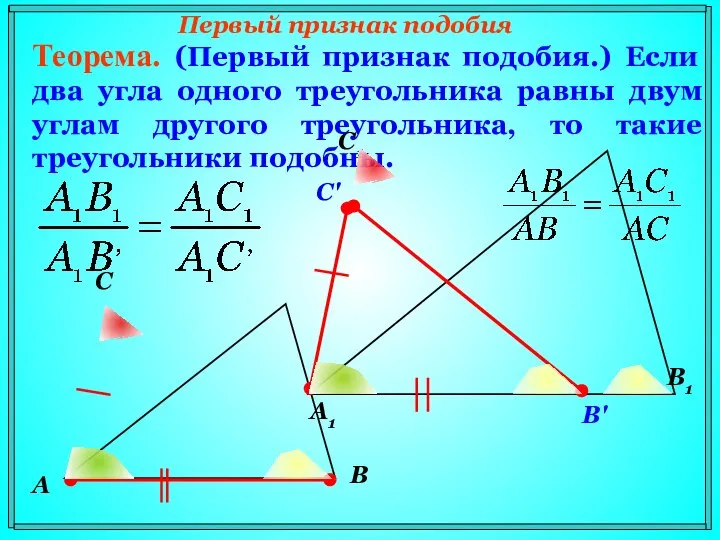
- 11. Первый признак подобия Теорема. (Первый признак подобия.) Если два угла одного треугольника равны двум углам другого
- 12. Теорема. (Первый признак подобия треугольников.) Если два угла одного треугольника равны двум углам другого треугольника, то
- 13. 2.Отложим: отрезок АВ'= А1В1 (т. В' є AB) прямую В'С' || ВС 1. 3.По теореме о
- 14. Подобны ли прямоугольные треугольники, если у одного из них есть угол 40о, а у другого 50о?
- 16. Скачать презентацию







 Математическая логика и теория алгоритмов
Математическая логика и теория алгоритмов Нахождение дроби от числа и числа по его дроби
Нахождение дроби от числа и числа по его дроби Обеспечение условий для максимально возможного раскрытия потенциала учащихся средствами математики
Обеспечение условий для максимально возможного раскрытия потенциала учащихся средствами математики Функции и их свойства. Область определения и область значений функции
Функции и их свойства. Область определения и область значений функции Прибавить и вычесть 2
Прибавить и вычесть 2 Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля
Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля  Найдите значение выражения
Найдите значение выражения Знаки сравнения и знак равенства
Знаки сравнения и знак равенства Презентация на тему Площадь четырёхугольника
Презентация на тему Площадь четырёхугольника  Теория преобразования графиков функций
Теория преобразования графиков функций Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Презентация на тему ГИА 2013 Модуль «Геометрия» № 9
Презентация на тему ГИА 2013 Модуль «Геометрия» № 9 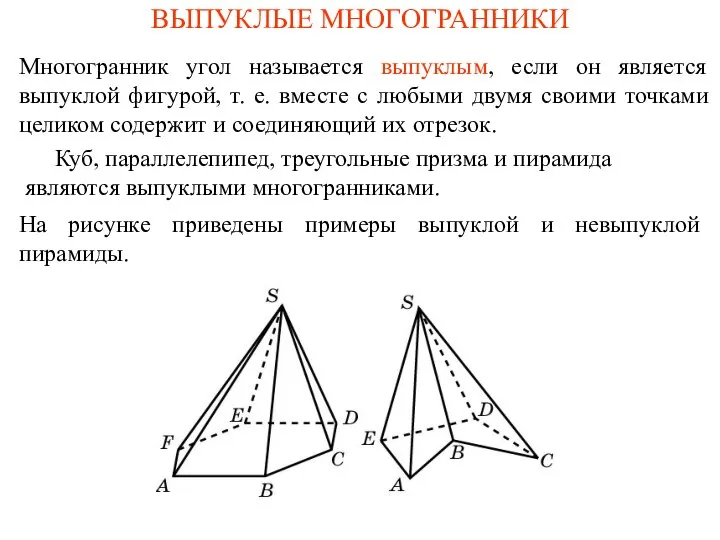 Выпуклые многогранники
Выпуклые многогранники Число и цифра 9
Число и цифра 9 Вычитание чисел. Математический тренажер
Вычитание чисел. Математический тренажер Методические рекомендации по изложению темы Площади плоских фигур по геометрии в 7 - 9 классах
Методические рекомендации по изложению темы Площади плоских фигур по геометрии в 7 - 9 классах Решение уравнений. Элективный курс. Алгебра 11 класс. Урок 2
Решение уравнений. Элективный курс. Алгебра 11 класс. Урок 2 Решение дробно-рациональных уравнений
Решение дробно-рациональных уравнений Проверка деления
Проверка деления Состав числа
Состав числа Мгновенное умножение
Мгновенное умножение Параллельные плоскости
Параллельные плоскости Логарифмическая функция. Свойства, график. Решение примеров
Логарифмическая функция. Свойства, график. Решение примеров Отношения и золотое сечение
Отношения и золотое сечение Уравнение с двумя переменными и его график
Уравнение с двумя переменными и его график Пирамида. Решение задач
Пирамида. Решение задач Площадь. Площадь прямоугольника
Площадь. Площадь прямоугольника mypresentation.ru
mypresentation.ru