Содержание
- 2. 1.Нахождение процентов от данного числа. Найти р % от числа А.
- 3. 2. Нахождение числа по данному числу его процентов. Найти всё число А, если р% это В.
- 4. 3.Нахождение процентного отношения двух чисел. Сколько процентов число А составляет от В.
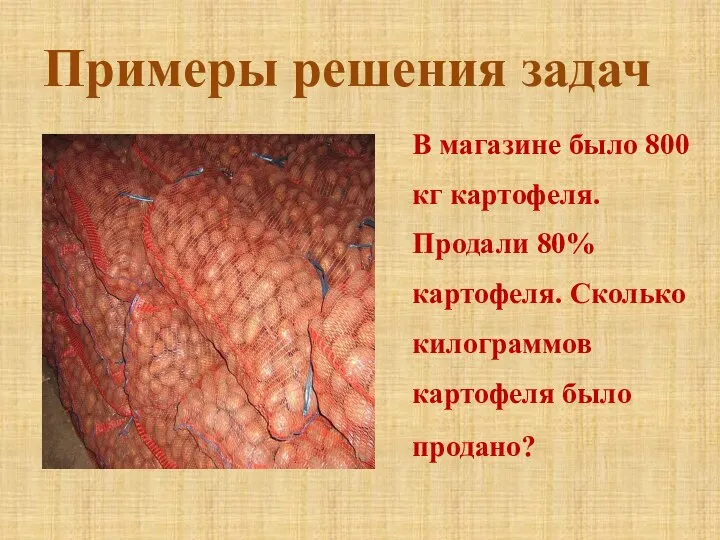
- 5. Примеры решения задач . В магазине было 800 кг картофеля. Продали 80% картофеля. Сколько килограммов картофеля
- 6. Способ 1. Решение: 1) 80% = 0,8 2) 800 · 0,8 = 640 кг Способ 2.
- 7. Готовясь к экзамену, студент решил 38 задач из сборника для самоподготовки. Что составляет 25% числа всех
- 8. Способ 1. Решение: 1) 25% = 0,25 2) 38:0,25= 152 Способ 2. 38:25=1,52 1,52·100=152 Ответ: 152
- 9. В классе 35 учеников. 14 из них – девочки. Сколько процентов девочек в классе?
- 11. Задачи на проценты на ОГЭ и ЕГЭ
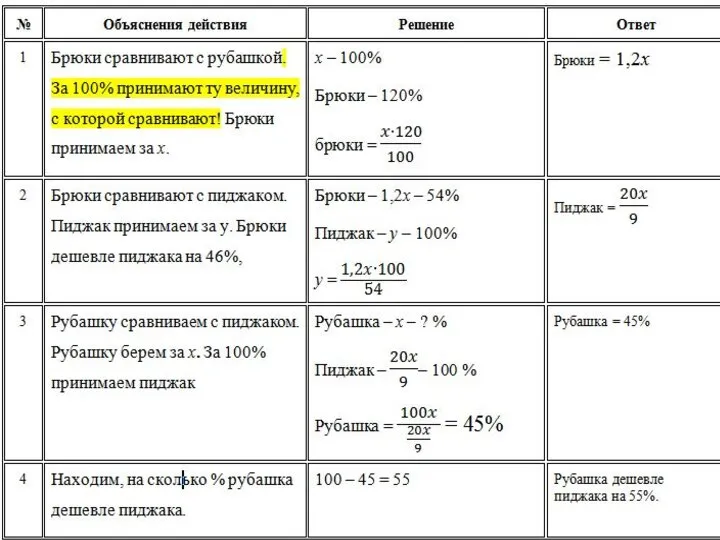
- 12. Брюки дороже на 20% рубашки и дешевле на 46% пиджака. На сколько % рубашка дешевле пиджака?
- 14. 100% Б = 120%Р = 54%П 120%Р = 54%П 20%Р = 9%П 100%Р = 45%П 100%
- 15. ЗАДАЧИ НА «СУШКУ»
- 17. Решение: 100-64 =36(%)-27 кг 27:0,36=75(кг) Ответ: 75 кг
- 18. Виноград содержит 90% влаги, а изюм - 5%. Сколько кг винограда надо взять для получения 20
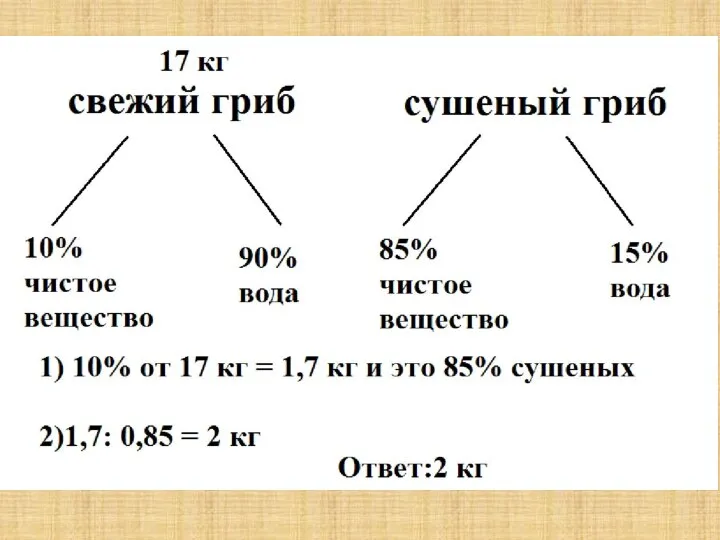
- 20. Свежий гриб содержит 90% воды, а сушеный – 15%. Сколько получится сушеных грибов из 17кг свежих?
- 22. Задачи, связанные с понятиями «концентрация» и «процентное содержание»
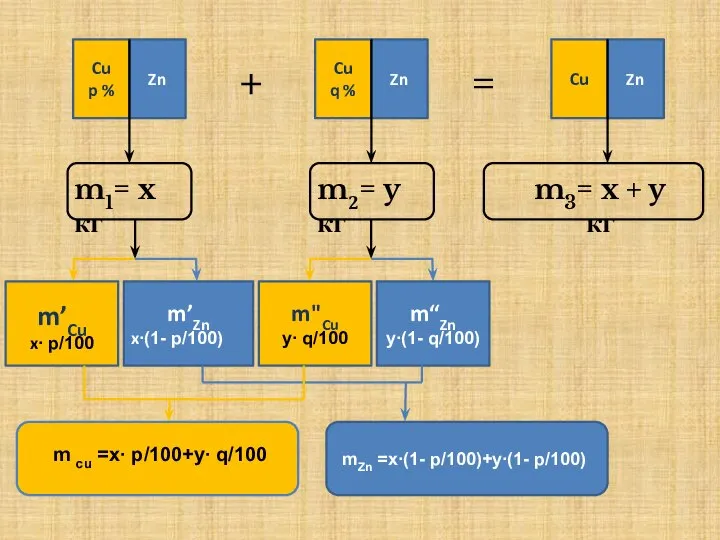
- 23. С – концентрация m = mA + mB + mC P – процентное содержание компоненты P
- 24. + = m’Zn x∙(1- p/100) m’Cu x∙ p/100 m"Cu y∙ q/100 m“Zn y∙(1- q/100)
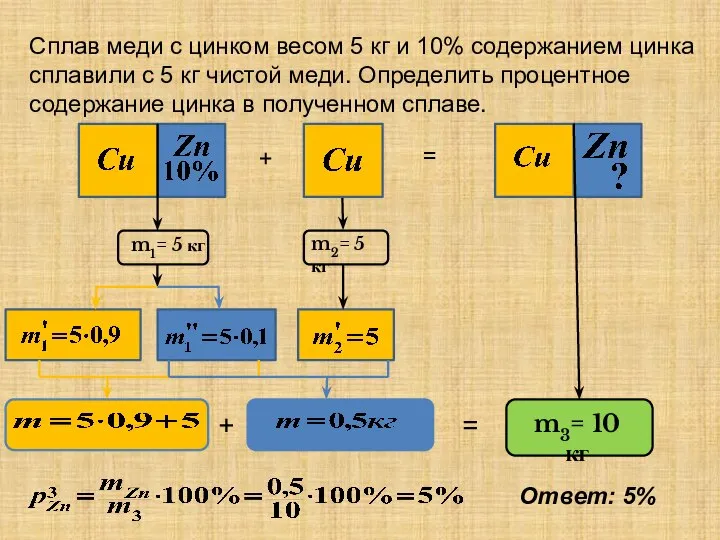
- 25. Сплав меди с цинком весом 5 кг и 10% содержанием цинка сплавили с 5 кг чистой
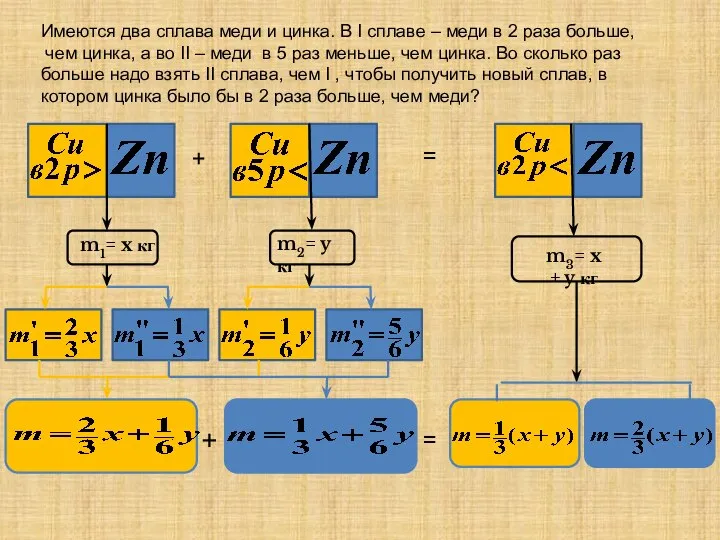
- 26. Имеются два сплава меди и цинка. В I сплаве – меди в 2 раза больше, чем
- 27. = = Ответ : в 2 раза
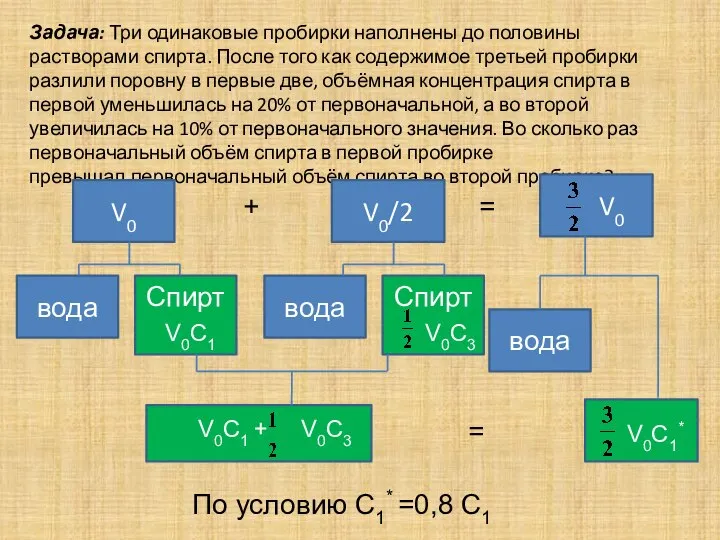
- 28. Задача: Три одинаковые пробирки наполнены до половины растворами спирта. После того как содержимое третьей пробирки разлили
- 29. Задача: Три одинаковые пробирки наполнены до половины растворами спирта. После того как содержимое третьей пробирки разлили
- 31. Скачать презентацию





















 Презентация на тему Разложение многочлена на множители 7 класс
Презентация на тему Разложение многочлена на множители 7 класс  Морской бой
Морской бой Комбинаторика. Правило умножения
Комбинаторика. Правило умножения Правило параллелепипеда
Правило параллелепипеда Углы. Тест
Углы. Тест Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного
Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного Таблица для мешка по двум признакам
Таблица для мешка по двум признакам Многогранники
Многогранники Задача №12. 9 класс
Задача №12. 9 класс Комбинаторные задачи
Комбинаторные задачи Презентация на тему Нахождение неизвестного по двум разностям
Презентация на тему Нахождение неизвестного по двум разностям  Числовая последовательность
Числовая последовательность Выражение длины вектора через его координаты
Выражение длины вектора через его координаты Практическое применение треугольников в жизни
Практическое применение треугольников в жизни Распределительное свойство умножения. Упрощение выражений
Распределительное свойство умножения. Упрощение выражений Решение задач на проценты. Повторение, обобщение
Решение задач на проценты. Повторение, обобщение Угол между прямой и плоскостью
Угол между прямой и плоскостью Урок-экскурсия по государственному историко-культурному музею-заповеднику Московский Кремль
Урок-экскурсия по государственному историко-культурному музею-заповеднику Московский Кремль Группа предметов. Множество. Элемент множества. 3 класс
Группа предметов. Множество. Элемент множества. 3 класс lobachevsky
lobachevsky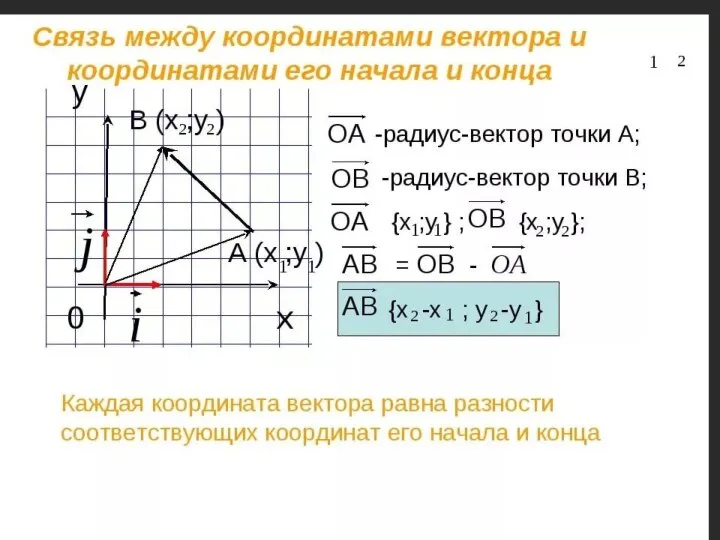 Векторы
Векторы Тестирование генераторов случайных чисел
Тестирование генераторов случайных чисел Состав числа 3 из двух слагаемых
Состав числа 3 из двух слагаемых Теорема. Франсуа Виет (1540-1603)
Теорема. Франсуа Виет (1540-1603) Площади. Формула Пика
Площади. Формула Пика Четырехзначные числа
Четырехзначные числа Равнобокая трапеция из бумаги. Работа ножницами
Равнобокая трапеция из бумаги. Работа ножницами Презентация на тему Первый признак равенства треугольников
Презентация на тему Первый признак равенства треугольников