Содержание
- 2. Все построения на плоскости производятся чертежными инструментами и построения получаются точными, а вот выполнять построения в
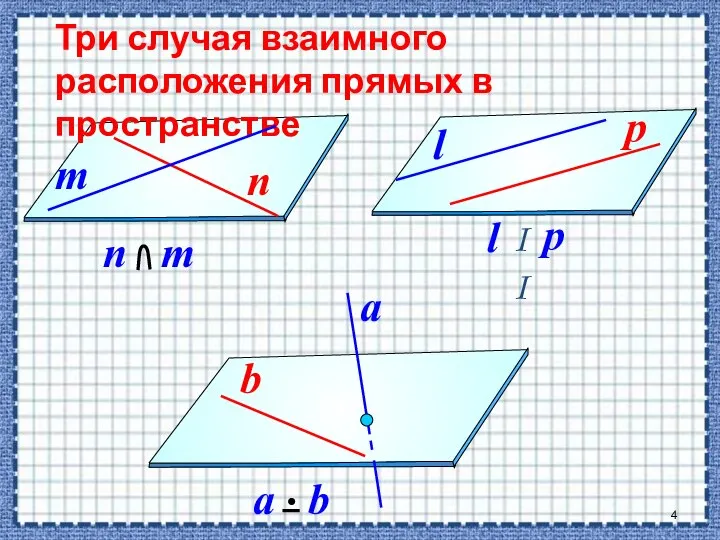
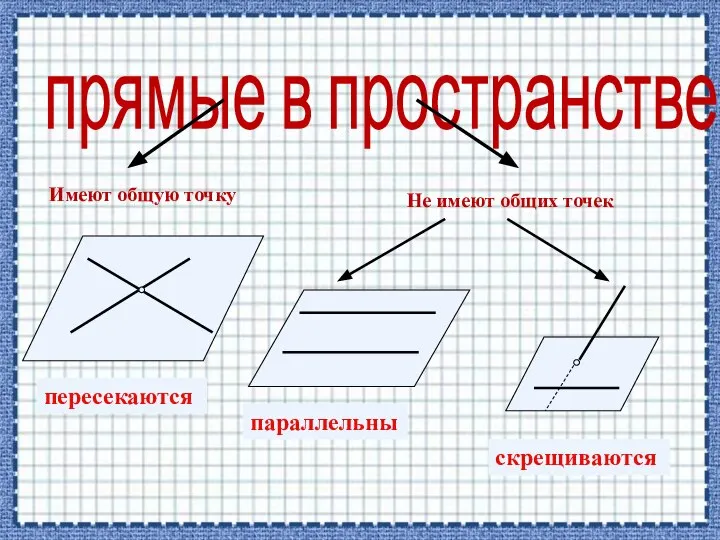
- 3. Возможные расположения прямых в пространстве:
- 4. Три случая взаимного расположения прямых в пространстве
- 5. прямые в пространстве
- 6. Определение: Две прямые называются параллельными, если они лежат в одной плоскости и не имеют общей точки
- 7. Задача: Через данную точку К провести прямую, параллельную данной прямой а Дано: К ∉ a Доказать:
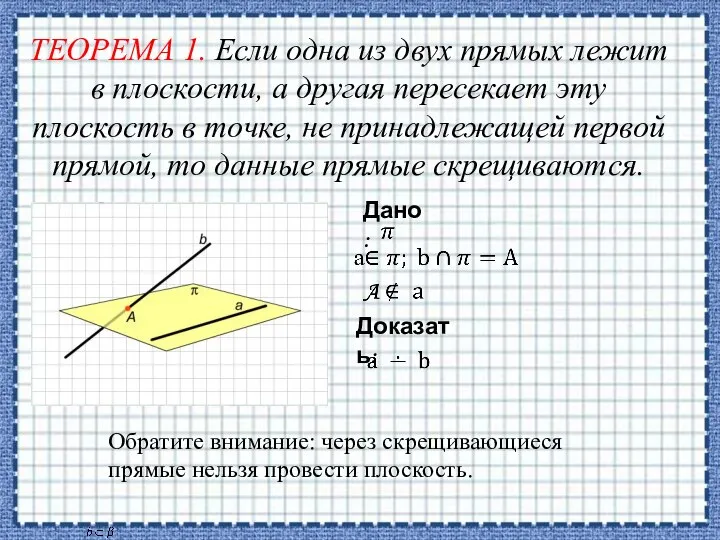
- 8. ТЕОРЕМА 1. Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в
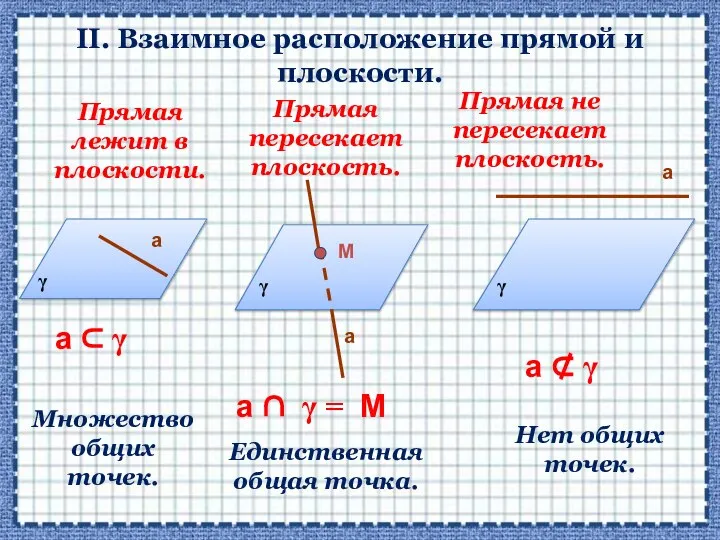
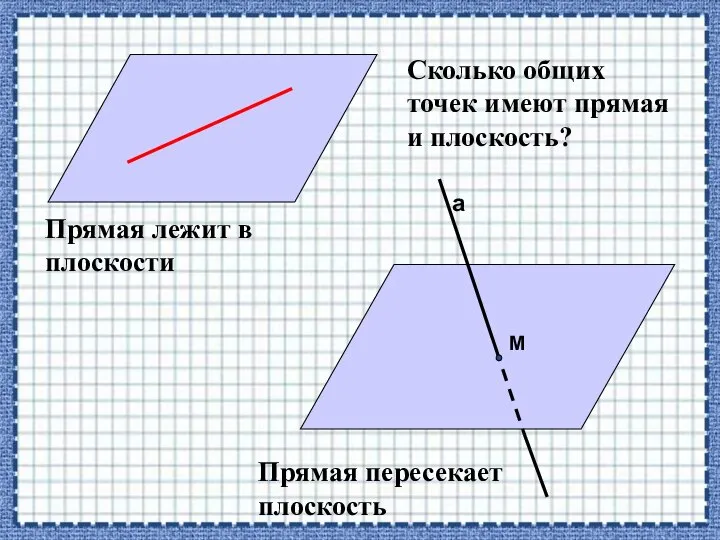
- 9. II. Взаимное расположение прямой и плоскости. Прямая лежит в плоскости. Прямая пересекает плоскость. Прямая не пересекает
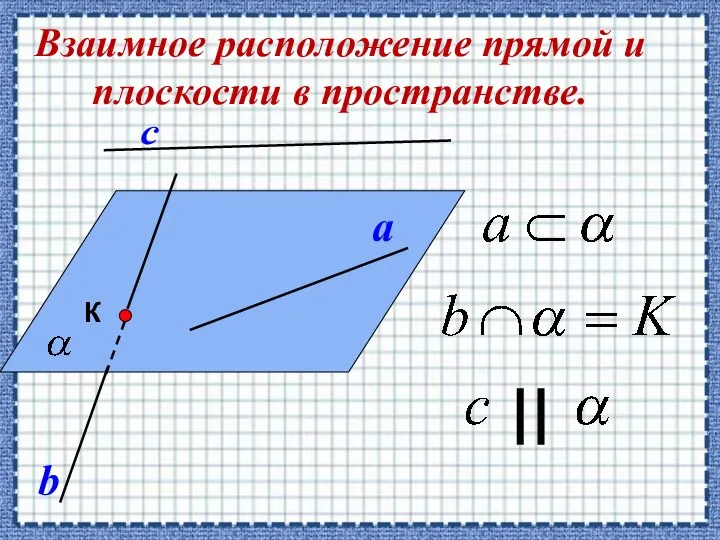
- 10. Взаимное расположение прямой и плоскости в пространстве.
- 11. Определение. Прямая и плоскость называются параллельными, если они не имеют общей точки или прямая лежит в
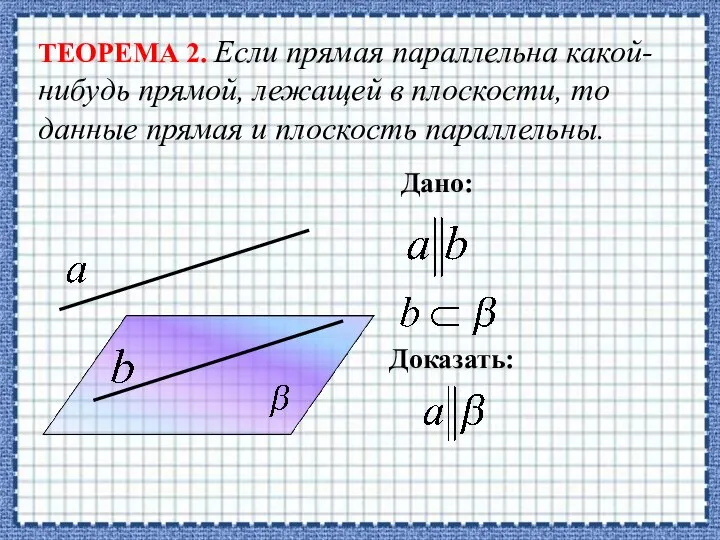
- 12. ТЕОРЕМА 2. Если прямая параллельна какой-нибудь прямой, лежащей в плоскости, то данные прямая и плоскость параллельны.
- 13. ТЕОРЕМА 3 (обратная) Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то
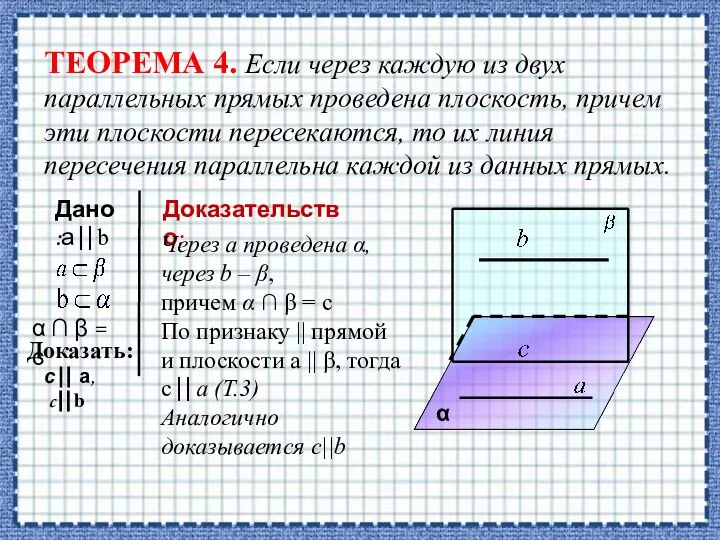
- 14. ТЕОРЕМА 4. Если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются, то
- 15. Доказательство: Рассмотрим случай. в, с ∈ β; а, с ∈ α 1. Возьмем т.М, М ∈
- 16. а М Прямая лежит в плоскости Прямая пересекает плоскость Сколько общих точек имеют прямая и плоскость?
- 17. Как в пространстве можно однозначно задать плоскость? 1. По трем точкам 2. По прямой и не
- 18. Задание 1 Вставьте пропущенные слова Единственную плоскость можно задать через три точки, при этом они на
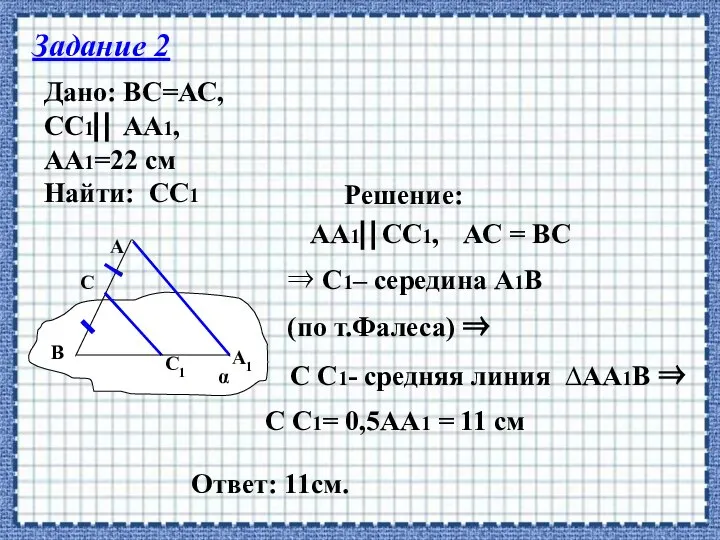
- 19. Задание 2 Дано: ВС=АС, СС1⎜⎜ АА1, АА1=22 см Найти: СС1 Решение: АА1⎜⎜СС1, АС = ВС ⇒
- 21. Скачать презентацию









 Цилиндр, конус, шар
Цилиндр, конус, шар Формулы сложения
Формулы сложения Решение логических задач
Решение логических задач Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Статистическая обработка измерений
Статистическая обработка измерений Экономическая статистика. Демография предприятий
Экономическая статистика. Демография предприятий Понятие многогранника
Понятие многогранника Щенок Пузырёк. Сложение и вычитание в пределах десяти
Щенок Пузырёк. Сложение и вычитание в пределах десяти Математические ребусы. 4 класс
Математические ребусы. 4 класс Преобразование графиков функций
Преобразование графиков функций Презентация на тему Признаки равенства и подобия треугольников
Презентация на тему Признаки равенства и подобия треугольников  Окружность
Окружность Центральные и вписанные углы
Центральные и вписанные углы Ряды
Ряды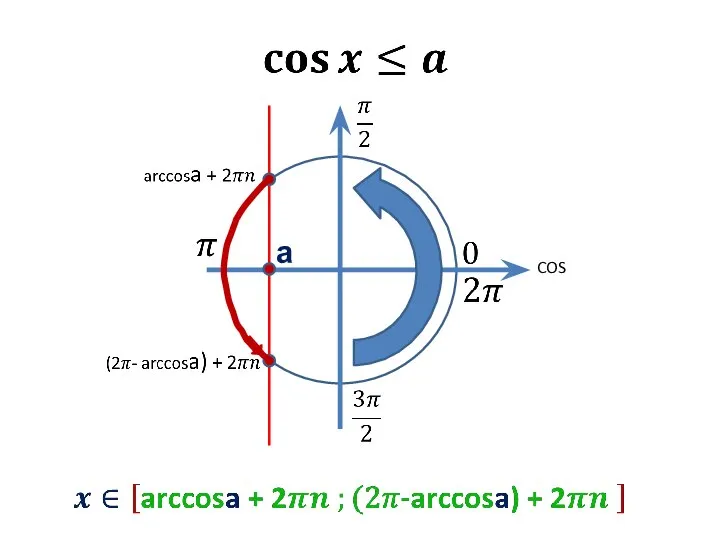 Неравенства вида Cos〖x≤a〗
Неравенства вида Cos〖x≤a〗 Устная работа. Разложите на множители
Устная работа. Разложите на множители обратные тригонометрические функции
обратные тригонометрические функции Логарифмические неравенства
Логарифмические неравенства Решение задач по теме: Четырехугольники
Решение задач по теме: Четырехугольники Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах
Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах Презентация на тему Решение систем неравенств (8 класс)
Презентация на тему Решение систем неравенств (8 класс)  Презентация на тему Исследование функции и построение графика (10 класс)
Презентация на тему Исследование функции и построение графика (10 класс)  Нахождение точек экстремума функции. 10 класс
Нахождение точек экстремума функции. 10 класс Поворот. Пример построения треугольника
Поворот. Пример построения треугольника Оснащение математических уголков в ДОУ
Оснащение математических уголков в ДОУ Математика ЕГЭ 2018 №7
Математика ЕГЭ 2018 №7 Дифференциальные уравнения. Лекция 2
Дифференциальные уравнения. Лекция 2 Сложение чисел с переходом через десяток в пределах 20. Помоги русалке
Сложение чисел с переходом через десяток в пределах 20. Помоги русалке