Слайд 2 Производная сложной функции

Слайд 4
2) случай двух независимых переменных .

Слайд 82) Случай двух независимых переменных

Слайд 10Частные производные высших порядков

Слайд 13Производная по направлению. Градиент.

Слайд 14Производная по направлению. Градиент.
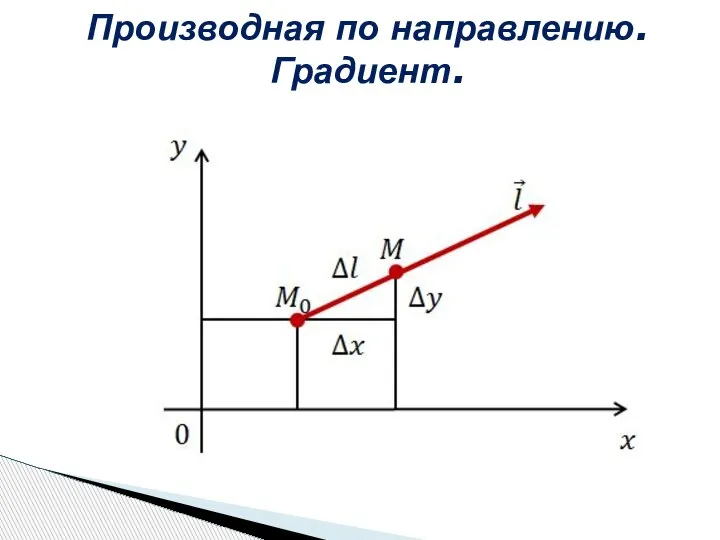
Слайд 15Производная по направлению. Градиент.

Слайд 18Производную функции одной переменной смело можно назвать производной по направлению – ведь

она характеризует скорость изменения функции в направлении оси .
И эта суть с учётом большего разнообразия направлений распространяется на производные функций нескольких переменных, в частности, на производные функции . Геометрически функция двух переменныхИ эта суть с учётом большего разнообразия направлений распространяется на производные функций нескольких переменных, в частности, на производные функции . Геометрически функция двух переменных чаще всего представляет собой поверхность, и значения «зет» у нас чётко ассоциируются с высотой. Таким образом, с позиций геометрии скорость изменения данной функции – есть скорость изменения высоты. При этом совершенно понятно, что «негоризонтальная» поверхность изменчива – в каких-то направлениях она крута, в каких-то полога, а где-то таки «равнина». И производная по направлению как раз призвана охарактеризовать «ландшафт местности» (скорость изменения функции) в различных точках по различным направлениям. В этой связи возникает первый вопрос:
Слайд 19
– это ЧИСЛО, характеризующее скорость изменения функции, причём:
– если , то

функция в точке по данному
направлению возрастает (поверхность «идёт в гору»);
– если , то функция в точке по данному направлению убывает («склон» поверхности);
– если , то функция в точке по данному направлению постоянна (поверхность параллельна плоскости ).
Слайд 20Механический и геометрический смысл производной по направлению

Слайд 22Свойства градиента
Если совсем просто, то куда «смотрит» градиент – там и

самый крутой «подъём в гору»
Слайд 24 Касательная плоскость и нормаль к поверхности.
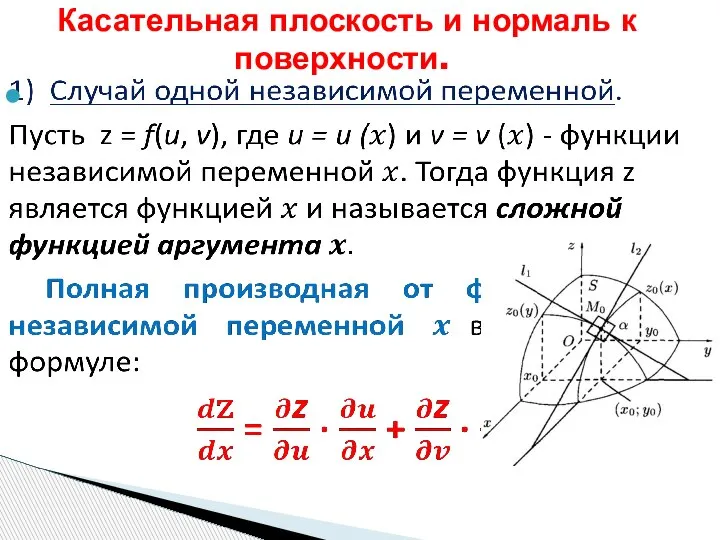
Слайд 25Опр. 2. Нормалью к поверхности называется перпендикуляр к касательной плоскости в точке


























 Приемы вычислений для случаев вида 26+7. 2 класс
Приемы вычислений для случаев вида 26+7. 2 класс Презентация на тему Цилиндр (11 класс)
Презентация на тему Цилиндр (11 класс)  Комбинация фигур
Комбинация фигур От перестановки множителей произведение не изменяется
От перестановки множителей произведение не изменяется Математическая викторина. Блок 1 и 2
Математическая викторина. Блок 1 и 2 Презентация
Презентация Презентация на тему Анализ геометрической формы предмета
Презентация на тему Анализ геометрической формы предмета  Числа, кратные 3
Числа, кратные 3 Преобразование графиков 9-10 классы
Преобразование графиков 9-10 классы Подготовка к изучению чисел
Подготовка к изучению чисел Иррациональные неравенства
Иррациональные неравенства Упрощение выражений (5 лкасс)
Упрощение выражений (5 лкасс) Построение сечений
Построение сечений Конус. Основные элементы конуса
Конус. Основные элементы конуса Понятие числовой окружности. Радианное измерение углов
Понятие числовой окружности. Радианное измерение углов Б. Кавальери и его метод неделимых
Б. Кавальери и его метод неделимых Квадрат. Прямоугольник
Квадрат. Прямоугольник Математический марафон
Математический марафон Презентация на тему НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ
Презентация на тему НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ  Состав чисел в приделах 10. Решение задач
Состав чисел в приделах 10. Решение задач Математка в жизни
Математка в жизни Lecture 7
Lecture 7 Семейство четырехугольников
Семейство четырехугольников Решение линейных уравнений
Решение линейных уравнений Линейная алгебра. Применение определителей
Линейная алгебра. Применение определителей Геометрическая оптика. 11 класс. ЕГЭ
Геометрическая оптика. 11 класс. ЕГЭ Решение задач на проценты
Решение задач на проценты Линейная алгебра и аналитическая геометрия
Линейная алгебра и аналитическая геометрия