Содержание
- 2. Цель урока: Формировать знания учащихся о множествах и его элементах, о пустом множестве, о способах задания
- 3. Понятия теории множеств Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно
- 4. Например: Множество цифр: 0;1;2;3;4;5;6;7;8;9 Множество букв русского алфавита Например: 1). Цифра 6 – элемент множества цифр.
- 5. Для обозначения множеств используют большие буквы латинского алфавита или фигурные скобки, внутри которых записывают элементы множества(при
- 6. Для обозначения элементов множества используют малые буквы латинского алфавита Например: 1). f = 6 – элемент
- 7. Множество может быть: 1). Конечное : Например: А— множество цифр 2). Бесконечное: Например: N – множество
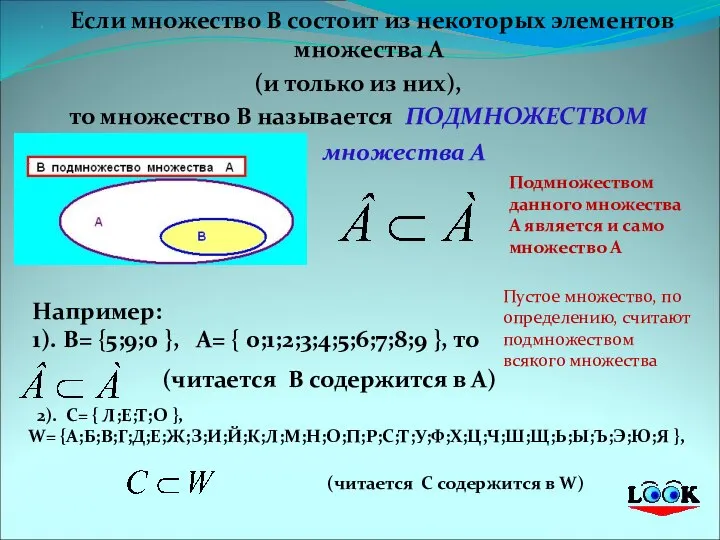
- 8. На диаграмме Эйлера-Венна утверждение "множество А является подмножеством множество В" изображают так Если множество В состоит
- 9. СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ Перечислением элементов множества; Описанием общего (характеристического) свойства, объединяющего элементы. Например: 1). К =
- 10. Множества называются РАВНЫМИ, если они состоят из одних и тех же элементов Например: 1). Равными являются
- 11. Решение задач 1.Задайте перечислением элементов множества: а) А—множество гласных букв русского алфавита. Решение А = {а,
- 12. 2. Перечислить элементы следующих множеств: а) А= {х : хє ученикам вашего класса, которые сейчас отсутствуют
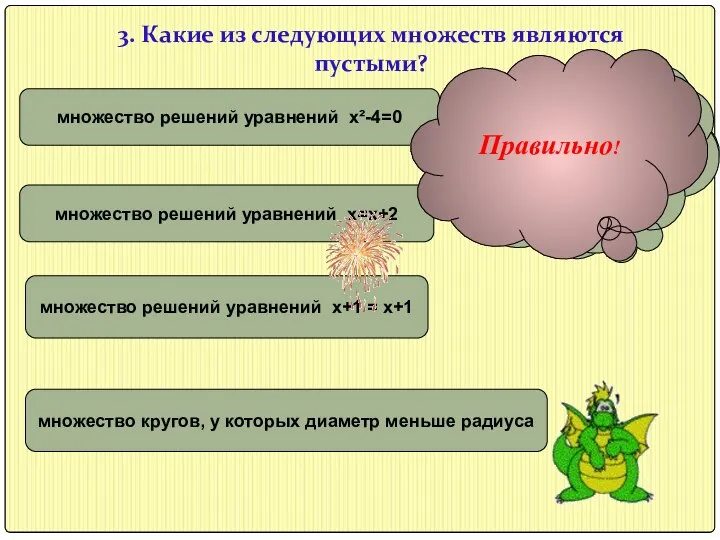
- 13. 3. Какие из следующих множеств являются пустыми? неверно множество решений уравнений х²-4=0 множество решений уравнений х=х+2
- 14. 5. Даны множества: а) множество А всех трапеций. б) множество В всех прямоугольников. в) множество С
- 15. Суммой, или объединением произвольного конечного или бесконечного множества множеств называется множество, состоящее из тех и только
- 16. ОБЪЕДИНЕНИЕ МНОЖЕСТВ А и В Например: L= { 5;7;9;3;1}, W= { 1;0;8;2;4;5;6 } => LUW={0;1;2;3;4;5;6;7;8;9} С
- 17. Пересечением любого конечного или бесконечного множества множеств называется множество, состоящее из тех и только тех элементов,
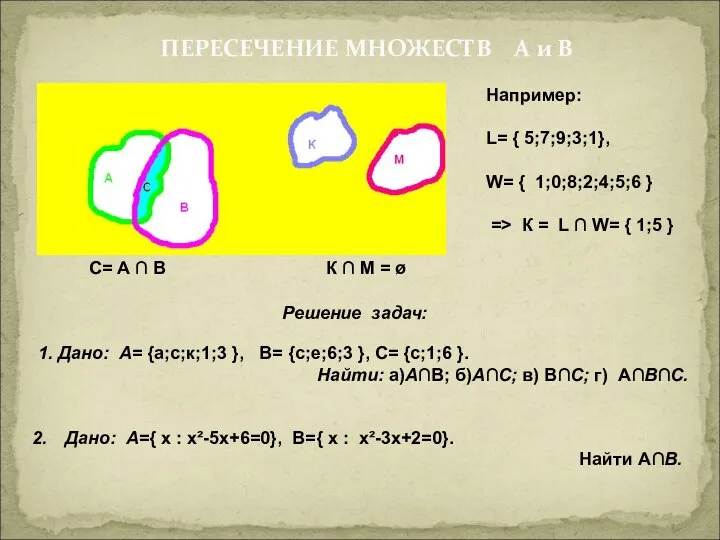
- 18. ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ А и В С= А ∩ В К ∩ М = ø Например: L=
- 19. Разностью между множеством В и множеством А называется множество всех элементов из В , не являющихся
- 20. РАЗНОСТЬ МНОЖЕСТВ А и В Решение задач: 1. Дано: M = { a;b;c;d } , N
- 21. Дополнением множества А называется множество, состоящее из всех элементов, не принадлежащих множеству А (но принадлежащих универсальному
- 22. Задача. Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский
- 23. Подведение итогов урока: Приведите примеры множеств. Какие бывают множества по количеству элементов? Как обозначаются множества? Как
- 25. Скачать презентацию



















 Готовимся к ЕГЭ. Геометрия в3, в6, в9
Готовимся к ЕГЭ. Геометрия в3, в6, в9 Нахождение процентов от числа
Нахождение процентов от числа Числа 1 – 10. Сложение и вычитание
Числа 1 – 10. Сложение и вычитание Применение производной
Применение производной Прямая и окружность
Прямая и окружность Способы построения параллельных прямых
Способы построения параллельных прямых Задачи на готовых чертежах (геометрия, 7 класс)
Задачи на готовых чертежах (геометрия, 7 класс) Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена
Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена Правильные многогранники
Правильные многогранники Возможности символьного вычисления в среде MatLab
Возможности символьного вычисления в среде MatLab Решение примеров
Решение примеров Современный урок: какой он?
Современный урок: какой он? Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе
Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе Презентация на тему Разность квадратов
Презентация на тему Разность квадратов  Графический способ решения систем уравнений
Графический способ решения систем уравнений Таблица умножения и деления с числом 7
Таблица умножения и деления с числом 7 Решение задач ОГЭ. Реальная математика, № 16
Решение задач ОГЭ. Реальная математика, № 16 Логарифмические уравнения
Логарифмические уравнения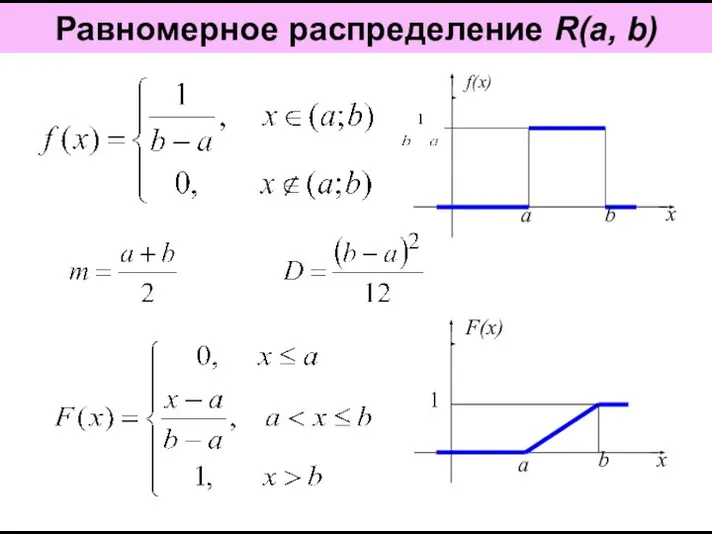 Равномерное распределение R(a, b)
Равномерное распределение R(a, b) Презентация на тему Решение текстовых задач различными способами
Презентация на тему Решение текстовых задач различными способами  Задачи математической статистики. Обработка данных
Задачи математической статистики. Обработка данных Презентация на тему Умножение и деление десятичных дробей на натуральные числа
Презентация на тему Умножение и деление десятичных дробей на натуральные числа  Разложение квадратного трёхчлена на множители
Разложение квадратного трёхчлена на множители Задачи по математике. 1 класс
Задачи по математике. 1 класс Презентация на тему ИЗМЕНЕНИЕ ВЕЛИЧИН
Презентация на тему ИЗМЕНЕНИЕ ВЕЛИЧИН  Элементы математической статистики, комбинаторики и теории вероятностей
Элементы математической статистики, комбинаторики и теории вероятностей Наибольшее и наименьшее значение функции. Примеры
Наибольшее и наименьшее значение функции. Примеры