Содержание
- 2. Одноканальная система обслуживания с очередью Система дифференциальных уравнений, описывающая поведение СМО: Для решения системы необходимо одно
- 3. Одноканальная система обслуживания с очередью Решение системы дифференциальных уравнений позволяет при заданных начальных условиях и известных
- 4. Одноканальная система обслуживания с очередью 1. Вероятность простоя системы: PПР = P0 6. Среднее количество заявок,
- 5. Задача П5-1. Одноканальная система обслуживания с очередью Определить, как изменятся среднее время пребывания заявки в системе
- 6. Одноканальная система обслуживания с очередью Задача П5-1. Из условий задачи интенсивность потока заявок λ =0,25 с-1
- 7. Одноканальная система обслуживания с очередью Задача П5-1. Интенсивность обслуживания во втором случае μ2 = 0,3 с-1.
- 8. Одноканальная система обслуживания с очередью Задача П5-1. Ответ: При увеличении интенсивности обслуживания заявок в канале с
- 9. Одноканальная система обслуживания с очередью Задача П5-2. Определить, как изменится вероятность отказа для одноканальной СМО без
- 10. Одноканальная система обслуживания с очередью Задача П5-2. Система линейных уравнений. Интенсивность обслуживания в первом случае μ1
- 11. Одноканальная система обслуживания с очередью Задача П5-3. Определить, как изменится вероятность отказа для одноканальной СМО без
- 12. Одноканальная система обслуживания с очередью Задача П5-4. Определить, как изменится вероятность отказа для одноканальной СМО в
- 13. Одноканальная система обслуживания с очередью Задача П5-4. При λ1 =0,25 с-1 и μ = 0,3 с-1
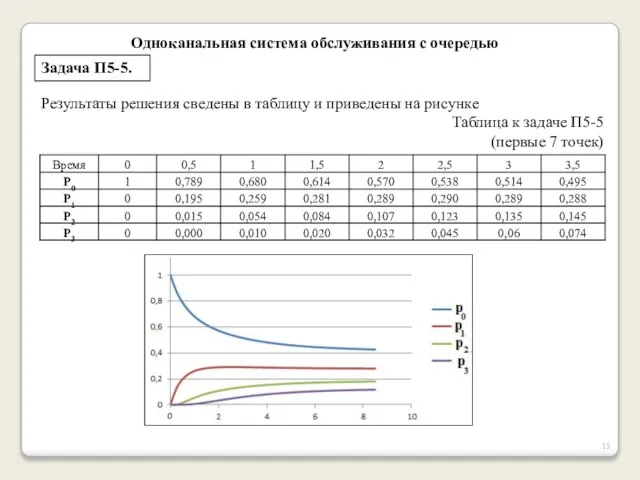
- 14. Одноканальная система обслуживания с очередью Задача П5-5. Рассмотреть изменение во времени вероятностей состояний одноканальной СМО с
- 15. Одноканальная система обслуживания с очередью Задача П5-5. Результаты решения сведены в таблицу и приведены на рисунке
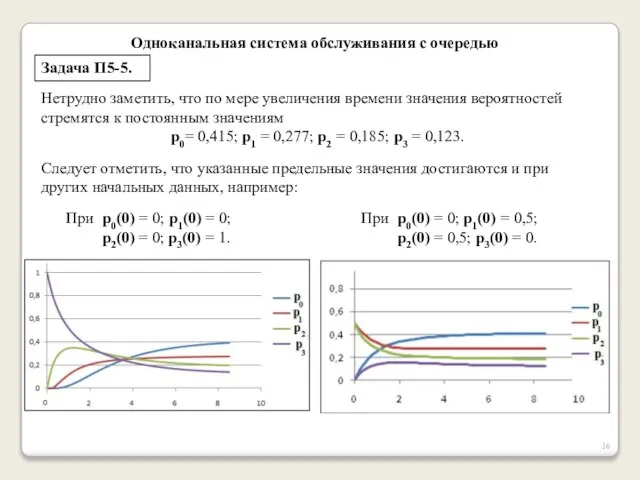
- 16. Одноканальная система обслуживания с очередью Задача П5-5. Нетрудно заметить, что по мере увеличения времени значения вероятностей
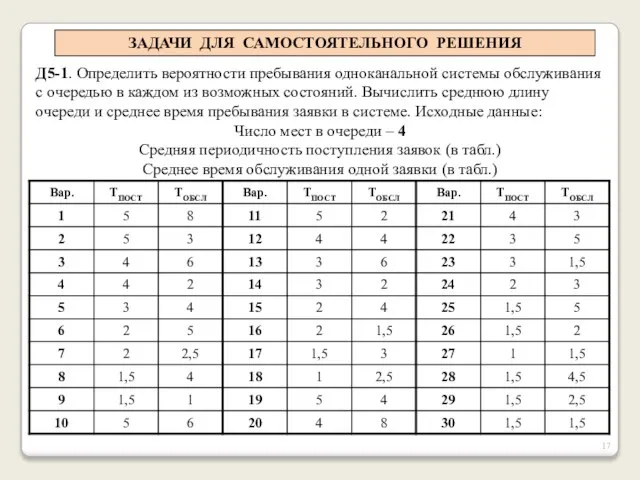
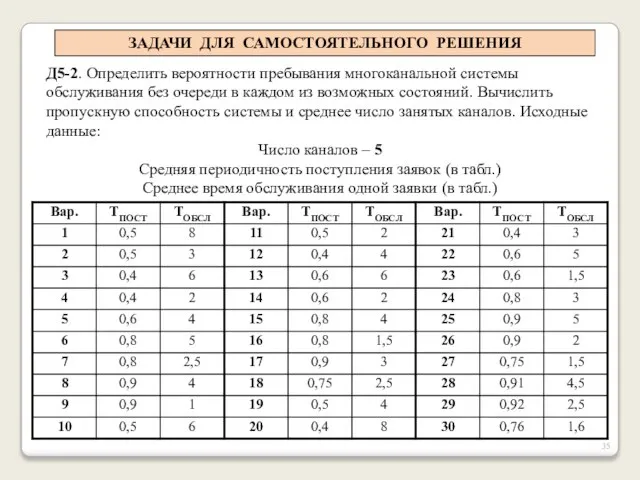
- 17. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ Д5-1. Определить вероятности пребывания одноканальной системы обслуживания с очередью в каждом из
- 18. Модели обслуживания вычислительных задач Раздел Многоканальные системы обслуживания без очереди
- 19. Многоканальная система обслуживания без очереди Теоретические основы. Граф состояний системы без очереди, которая имеет S одинаковых
- 20. Многоканальная система обслуживания без очереди 1. Вероятность простоя системы: PПР = P0 5. Среднее число занятых
- 21. Многоканальная система обслуживания без очереди Задача П5-6. Определить, как изменятся пропускная способность, занятость каналов и среднее
- 22. Многоканальная система обслуживания без очереди Задача П5-6. Из условий задачи λ = 0,5 с-1; μ1 =
- 23. Многоканальная система обслуживания без очереди Задача П5-6. Рассчитаем параметры системы при увеличенной производительности каналов μ2 =
- 24. Многоканальная система обслуживания без очереди Задача П5-6. Ответ. При увеличении интенсивности обслуживания заявок в канале с
- 25. Многоканальная система обслуживания без очереди Задача П5-7. Определить, как изменятся основные параметры СМО без очереди в
- 26. Многоканальная система обслуживания без очереди Задача П5-7. Система линейных уравнений. Система может иметь два возможных состояния:
- 27. Многоканальная система обслуживания без очереди Задача П5-7. 2. В системе два канала. Система может иметь три
- 28. Многоканальная система обслуживания без очереди Задача П5-7. 3. В системе три канала. Данный случай рассмотрен в
- 29. Многоканальная система обслуживания без очереди Задача П5-8. Определить, как изменится вероятность отказа четырехканальной СМО без очереди
- 30. Многоканальная система обслуживания без очереди Задача П5-8. Рассмотрим стационарное состояние системы при λ1 = 0,25 с-1;
- 31. Многоканальная система обслуживания без очереди Задача П5-8. Рассмотрим стационарное состояние системы при λ2 = 0,75 с-1;
- 32. Многоканальная система обслуживания без очереди Задача П5-9. СМО без очереди, имеющая три канала с интенсивностью обслуживания
- 33. Многоканальная система обслуживания без очереди Задача П5-9. Составим систему дифференциальных уравнений для новой интенсивности потока заявок,
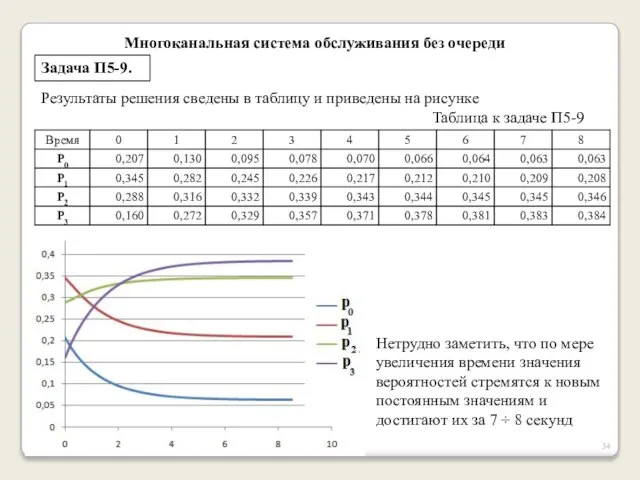
- 34. Многоканальная система обслуживания без очереди Задача П5-9. Результаты решения сведены в таблицу и приведены на рисунке
- 35. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ Д5-2. Определить вероятности пребывания многоканальной системы обслуживания без очереди в каждом из
- 36. Модели обслуживания вычислительных задач Раздел Многоканальные системы обслуживания с очередью
- 37. Многоканальная система обслуживания с очередью Теоретические основы. Граф состояний системы, которая имеет S одинаковых каналов и
- 38. Многоканальная система обслуживания с очередью Показатели эффективности СМО 1. Вероятность простоя, вероятность отказа, и вероятность обслуживания
- 39. Многоканальная система обслуживания с очередью Задача П5-10. Определить, как изменится вероятность отказа, если у четырехканальной СМО
- 40. Многоканальная система обслуживания с очередью Задача П5-10. Граф двухканальной системы с двумя местами в очереди будет
- 41. Многоканальная система обслуживания с очередью Задача П5-11. Имеется двухканальная СМО с двумя местами в очереди, описанная
- 42. Многоканальная система обслуживания с очередью Задача П5-11. Рассмотрим случай увеличения числа каналов. Допустим имеем систему, с
- 43. Многоканальная система обслуживания с очередью Задача П5-11. Для определения вероятностей состояний СМО следует записать систему из
- 44. Многоканальная система обслуживания с очередью Задача П5-11. Параметры эффективности трехканальной СМО с двумя местами в очереди:
- 45. Многоканальная система обслуживания с очередью Задача П5-11. Рассмотрим случай увеличения числа мест в очереди. Теперь будем
- 46. Многоканальная система обслуживания с очередью Задача П5-11. Для определения вероятностей состояний СМО следует записать систему из
- 47. Многоканальная система обслуживания с очередью Задача П5-11. Параметры эффективности двухканальной СМО с тремя местами в очереди:
- 48. Многоканальная система обслуживания с очередью Задача П5-12. Определить среднее время пребывания автомобилиста на заправке, если на
- 49. Многоканальная система обслуживания с очередью Граф системы будет иметь вид: Задача П5-12. Исходя из заданной периодичности
- 50. Многоканальная система обслуживания с очередью Задача П5-12. Вероятность того, что автомобилист откажется от обслуживания на данной
- 51. Модели обслуживания вычислительных задач Прочие виды многоканальных систем обслуживания
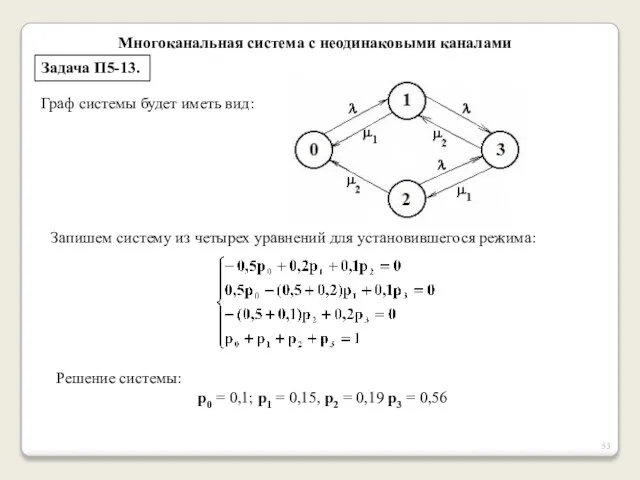
- 52. Многоканальная система с неодинаковыми каналами Задача П5-13. Рассмотреть параметры работы двухканальной СМО без очереди, если производительность
- 53. Многоканальная система с неодинаковыми каналами Задача П5-13. Граф системы будет иметь вид: Запишем систему из четырех
- 55. Скачать презентацию














































 Математический маятник. Измерения
Математический маятник. Измерения Признаки равенства треугольников
Признаки равенства треугольников Пропорция
Пропорция Решение текстовых задач
Решение текстовых задач Цифра ноль
Цифра ноль Решение планиметрических задач на стереометрических чертежах
Решение планиметрических задач на стереометрических чертежах Решение задач с помощью уравнений
Решение задач с помощью уравнений Число и цифра 5
Число и цифра 5 Презентация на тему Решение задач различными способами
Презентация на тему Решение задач различными способами  Число π. Длина окружности
Число π. Длина окружности Теория игр
Теория игр Вычисление площадей
Вычисление площадей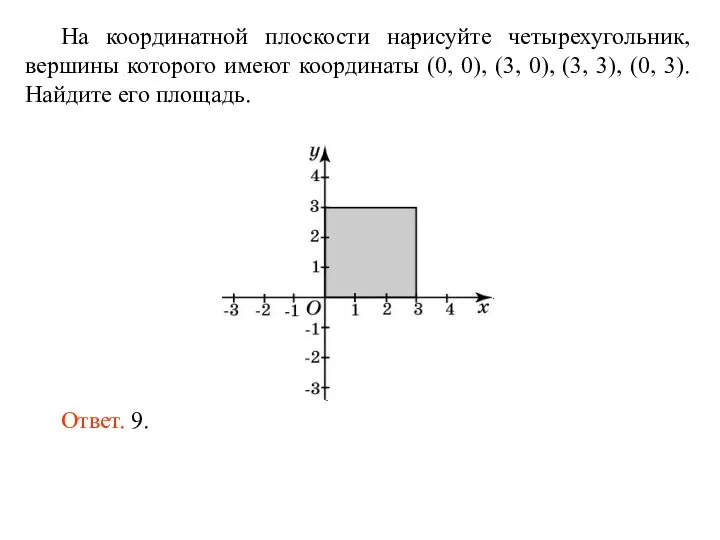 Площадь фигур на координатной плоскости
Площадь фигур на координатной плоскости Распределительная логистика. Практическое задание №8
Распределительная логистика. Практическое задание №8 Окружность. Методическая разработка урока
Окружность. Методическая разработка урока История дробей
История дробей Наибольшие и найменьшее значение функции
Наибольшие и найменьшее значение функции Prezentatsia_k_uroku_matematiki_6_klass
Prezentatsia_k_uroku_matematiki_6_klass Случаи вычитания 11-
Случаи вычитания 11- Функция. Свойства функции
Функция. Свойства функции Решите систему неравенств и укажите все целые числа, которые являются ее решениями
Решите систему неравенств и укажите все целые числа, которые являются ее решениями Математика в профессиях
Математика в профессиях Симметрия
Симметрия Взятие Измаила в математических и исторических нюансах
Взятие Измаила в математических и исторических нюансах Векторы. Решение задач
Векторы. Решение задач Числа 1 - 4. (1 класс)
Числа 1 - 4. (1 класс) Треугольник
Треугольник Четность, нечетность синуса, косинуса, тангенса, котангенса
Четность, нечетность синуса, косинуса, тангенса, котангенса