Содержание
- 2. 2. Доказательство Дж. Гардфилда (1882 г.) Расположим два равных прямоугольных треугольника так, чтобы катет одного из
- 3. 3. Доказательство простейшее Это доказательство получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и
- 4. 4. Старейшее доказательство Пусть АВСD квадрат, сторона которого равна гипотенузе прямоугольного треугольника АВЕ (АВ = с,
- 5. 5. Доказательство древних индусов Квадрат со стороной (a+b), можно разбить на части либо как на рисунке
- 7. Скачать презентацию




 Сечение поверхностей плоскостью
Сечение поверхностей плоскостью Тест по математике Именованные числа
Тест по математике Именованные числа Исследование на принадлежность классам функцию. Практическая работа
Исследование на принадлежность классам функцию. Практическая работа Черчение геометрических фигур не отрывая карандаш от бумаги
Черчение геометрических фигур не отрывая карандаш от бумаги Тест. Толерантность + Математика
Тест. Толерантность + Математика Полезные функции
Полезные функции Действительные числа и преобразования алгебраических выражений (домашнее задание)
Действительные числа и преобразования алгебраических выражений (домашнее задание) Усный счет
Усный счет Решение задач на проценты
Решение задач на проценты Рівняння. Основні властивості рівняння
Рівняння. Основні властивості рівняння Подобие треугольников. Второй признак
Подобие треугольников. Второй признак Параллелограмм и его свойства и признаки
Параллелограмм и его свойства и признаки Решение задач на свойства
Решение задач на свойства Тела вращения
Тела вращения Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Способы быстрого счета
Способы быстрого счета Возведение в куб суммы и разности
Возведение в куб суммы и разности Задачи с величинами: цена, количество, стоимость
Задачи с величинами: цена, количество, стоимость Показательная и логарифмическая функции
Показательная и логарифмическая функции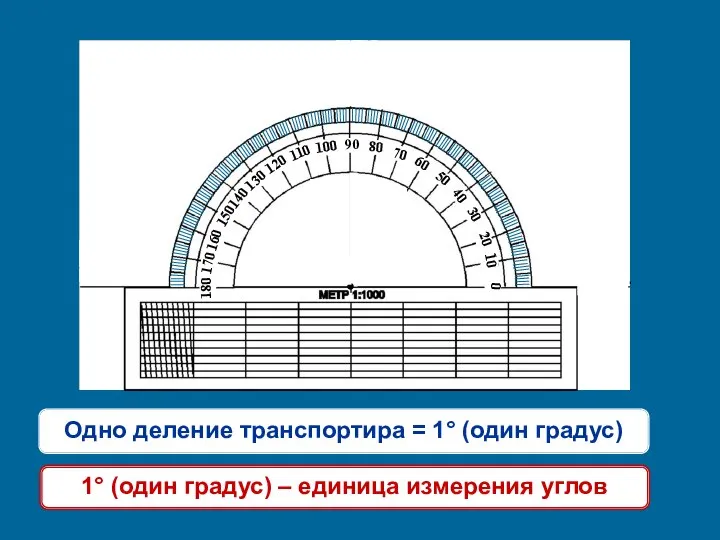 Измерение углов, транспортир
Измерение углов, транспортир Рівняння дотичної до графіка функції
Рівняння дотичної до графіка функції Ощущение тайны – наиболее прекрасное из доступных нам переживаний. Именно это чувство стоит у колыбели истинного искусства и нас
Ощущение тайны – наиболее прекрасное из доступных нам переживаний. Именно это чувство стоит у колыбели истинного искусства и нас Презентация на тему Небесная геометрия - снежинки
Презентация на тему Небесная геометрия - снежинки  Взаимное расположение прямой и окружности. Касательная
Взаимное расположение прямой и окружности. Касательная Задания на логическое мышление
Задания на логическое мышление Презентация на тему Решение задач различными способами
Презентация на тему Решение задач различными способами  Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями Вероятность и статистика
Вероятность и статистика