Содержание
- 2. Натуральные числа Числа, которые используются для счета предметов: 1, 2, 3, ... . N = {1,
- 3. Целые числа Натуральные числа 1, 2, 3, ..., противоположные им числа и число 0 образуют множество
- 4. Рациональные числа Числа, которые можно представить в виде , где , называют рациональными. Множество рациональных чисел
- 5. Иррациональные числа Числа, которые нельзя представить в виде , где называют иррациональными. Иррациональные числа – бесконечные
- 6. Действительные числа Объединение рациональных и иррациональных чисел называют действительными числами. Множество действительных чисел обозначают символом R.
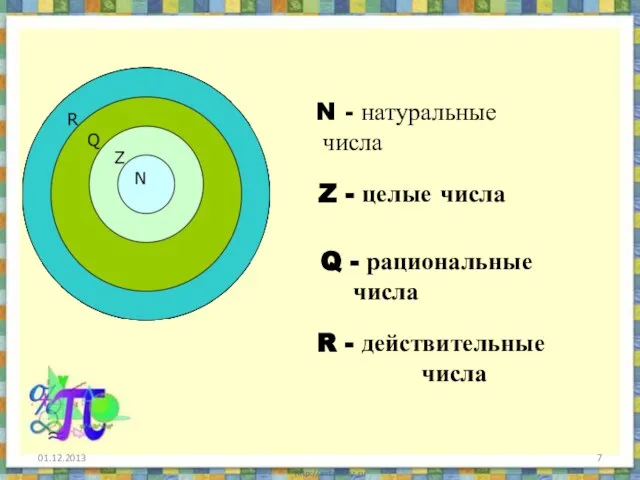
- 7. 01.12.2013 N - натуральные числа Z - целые числа Q - рациональные числа R - действительные
- 8. Мнемоническое правило записи бесконечной десятичной периодической дроби в виде обыкновенной дроби Для того чтобы записать периодическую
- 9. Пример1. Запишите периодическую десятичную дробь в виде обыкновенной дроби: 2,1(45 ). Решение: Обозначим дробь буквой х:
- 11. Скачать презентацию







 Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Геометрия в искусстве
Геометрия в искусстве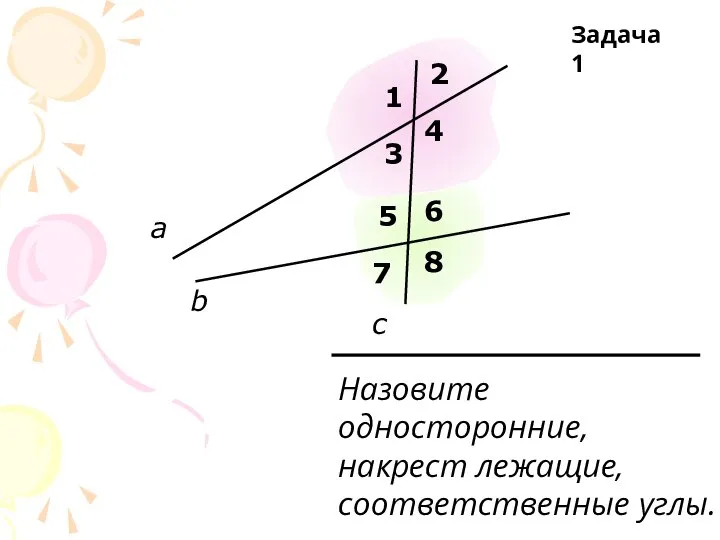 55 задач по теме параллельность
55 задач по теме параллельность Тела вращения. Цилиндр
Тела вращения. Цилиндр Действия с десятичными дробями 5 класс
Действия с десятичными дробями 5 класс Уравнение tg x =a
Уравнение tg x =a Предел последовательности. Бесконечно убывающая геометрическая прогрессия
Предел последовательности. Бесконечно убывающая геометрическая прогрессия Симметрия, как она есть
Симметрия, как она есть Своя игра. Треугольники
Своя игра. Треугольники Презентация на тему Приведение дробей к общему знаменателю
Презентация на тему Приведение дробей к общему знаменателю  Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения  Генеральная средняя
Генеральная средняя Экспресс-подготовка к ЗНО по математике
Экспресс-подготовка к ЗНО по математике Векторы в пространстве
Векторы в пространстве Презентация на тему Урок по теме «Координатная плоскость» 6 класс
Презентация на тему Урок по теме «Координатная плоскость» 6 класс  Решение задач по теме Параллелограмм
Решение задач по теме Параллелограмм Первый признак равенства треугольников
Первый признак равенства треугольников Организация экспериментов с использованием системных принципов
Организация экспериментов с использованием системных принципов Развёртка, как основа объёмной конструкции
Развёртка, как основа объёмной конструкции Алгоритмы решения простейших тригонометрических неравенств
Алгоритмы решения простейших тригонометрических неравенств Геометрические фигуры (открытый урок - игра Поле чудес)
Геометрические фигуры (открытый урок - игра Поле чудес) Теорема Пифагора
Теорема Пифагора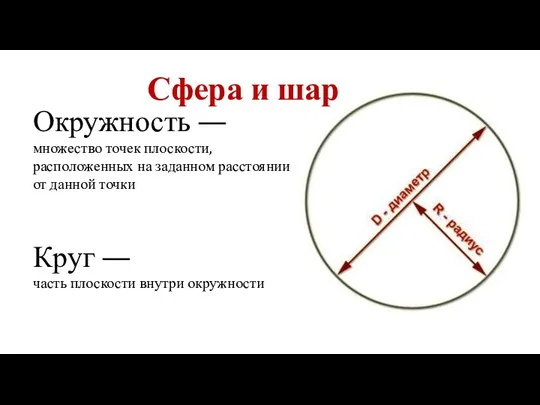 Сфера и шар
Сфера и шар Презентация на тему Принцесса математики Софья Ковалевская
Презентация на тему Принцесса математики Софья Ковалевская  Множество и его элементы
Множество и его элементы Презентация на тему Уравнения
Презентация на тему Уравнения  Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля
Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля Площадь прямоугольника
Площадь прямоугольника