Содержание
- 2. Событие называется случайным, если нельзя утверждать, что это событие в данных обстоятельствах непременно произойдет. А={в следующем
- 3. Невозможные события - события, которые в данных условиях произойти не могут. F={ npu бросании кубика выпадет
- 8. Совместные и несовместные события Совместные события могут происходить в данных условиях одновременно. Несовместные события НЕ могут
- 9. Пример: Совместные события: «наступило утро», «пошел снег». Несовместные события: : «наступило утро», «наступил вечер». 6
- 12. Случайные опыты те условия и действия, при которых может осуществиться случайное событие, принято называть случайным опытом,
- 13. Элементарные события События которые нельзя разделить на более простые , называются элементарными событиями. 5
- 14. Пример: Опыт: подбрасывание одной игральной кости Элементарные события: «выпало одно очко», «выпало два очка», «выпало три
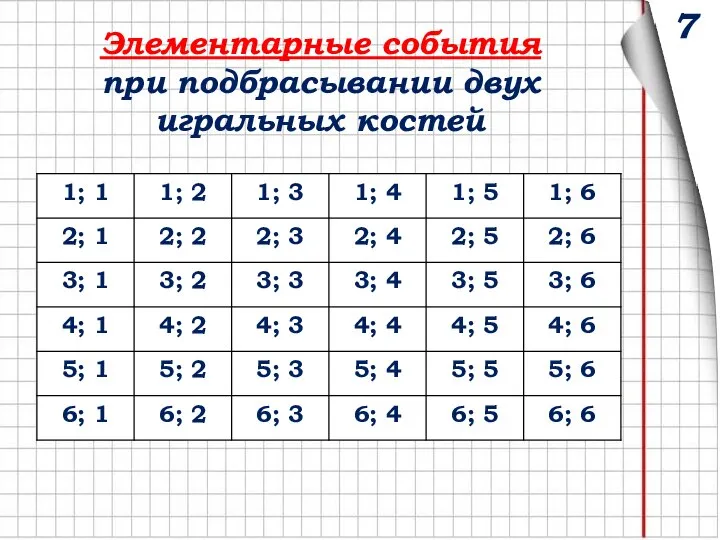
- 15. Пример: Опыт: подбрасывают две игральные кости. Элементарные события: (1;1); (1;2)…. (2;1); (2;2)… Элементарным событием при двух
- 16. Элементарные события при подбрасывании двух игральных костей 7
- 17. Равновозможные элементарные события Равновозможные элементарные события – это элементарные события шансы которых одинаковы. 8
- 18. Примеры: 1. При бросании одной игральной кости равновозможных элементарных событий 6. 2. При бросании двух игральных
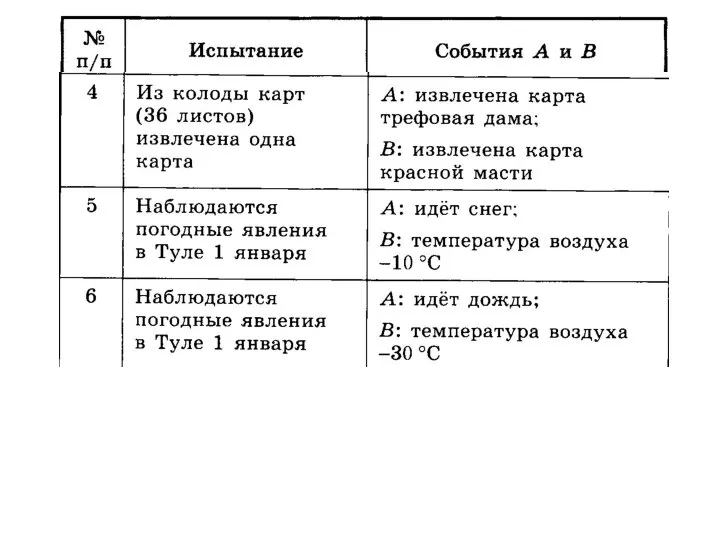
- 21. Пример. Что вероятнее: А={получить шестерку при подбрасывании кубика} или В={вытянуть шестерку из перетасованной колоды карт}? Шестерок
- 22. Таким образом, долю успеха того или иного события математики стали называть ВЕРОЯТНОСТЬЮ этого события и обозначать
- 23. Вероятности элементарных событий Вероятность равновозможных элементарных событий: Р(А)=1/N, где А- элементарное событие, N- число равновозможных элементарных
- 24. Пример: Все элементарные события случайного эксперимента равновозможны. Найдите вероятность каждого элементарного события, если их общее число
- 25. В каждом опыте сумма вероятностей всех элементарных событий равна 1. Пример: Рассмотрим случайный эксперимент, в котором
- 26. В каждом опыте сумма вероятностей всех элементарных событий равна 1. Пример: Рассмотрим случайный эксперимент, в котором
- 27. Благоприятствующие элементарные события Элементарные события, при которых наступает событие А, называются элементарными событиями, благоприятствующими событию А.
- 28. Пример: Опыт: бросание одной игральной кости. Событие А: «Выпало четное число очков» Благоприятствующие события: «выпало 2
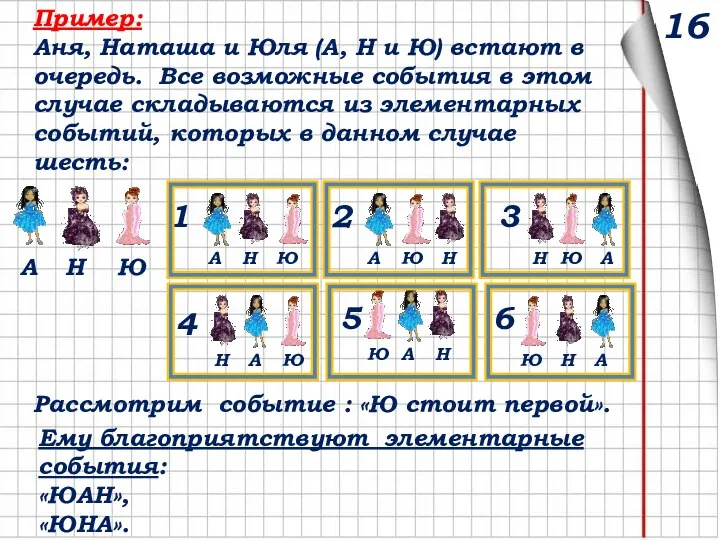
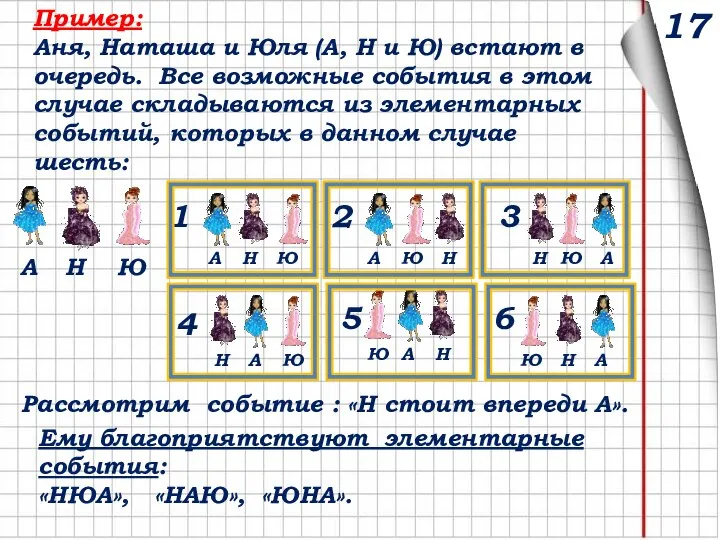
- 29. Пример: Аня, Наташа и Юля (А, Н и Ю) встают в очередь. Все возможные события в
- 30. Пример: Аня, Наташа и Юля (А, Н и Ю) встают в очередь. Все возможные события в
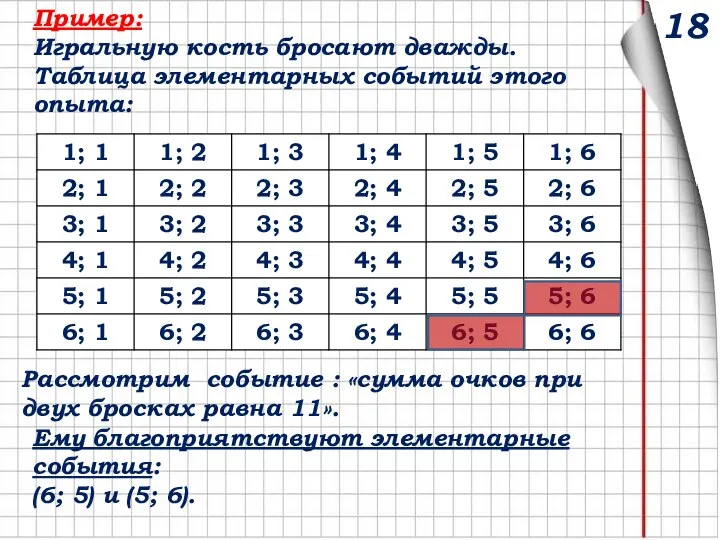
- 31. Пример: Игральную кость бросают дважды. Таблица элементарных событий этого опыта: Рассмотрим событие : «сумма очков при
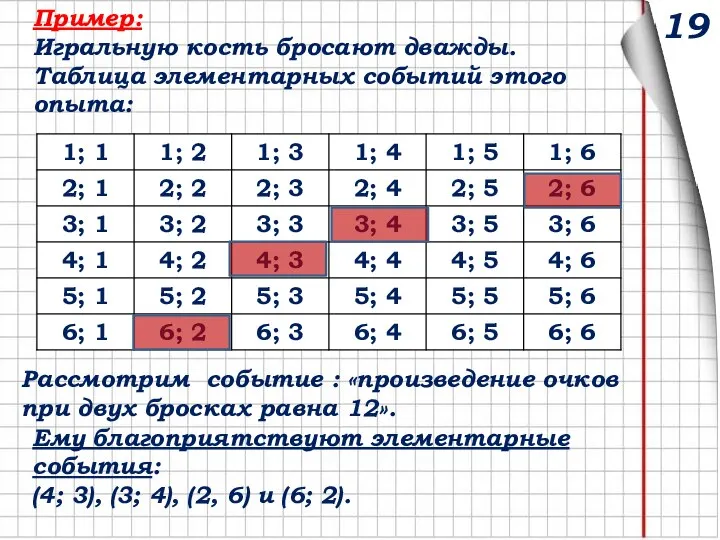
- 32. Пример: Игральную кость бросают дважды. Таблица элементарных событий этого опыта: Рассмотрим событие : «произведение очков при
- 33. а) если Р(А)=0, то события называются невозможными; b) если Р(А)=1, то события называются достоверными; с) для
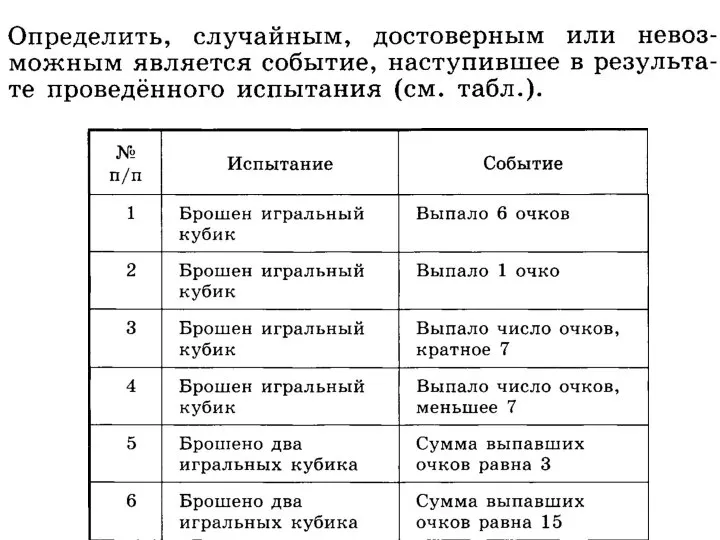
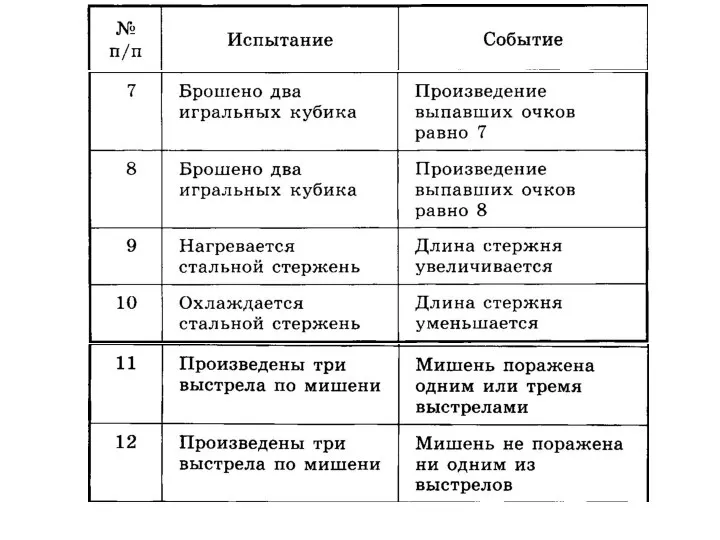
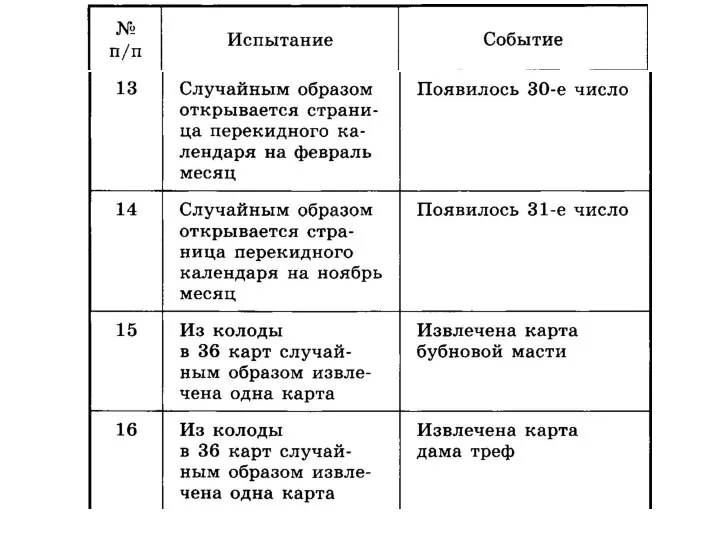
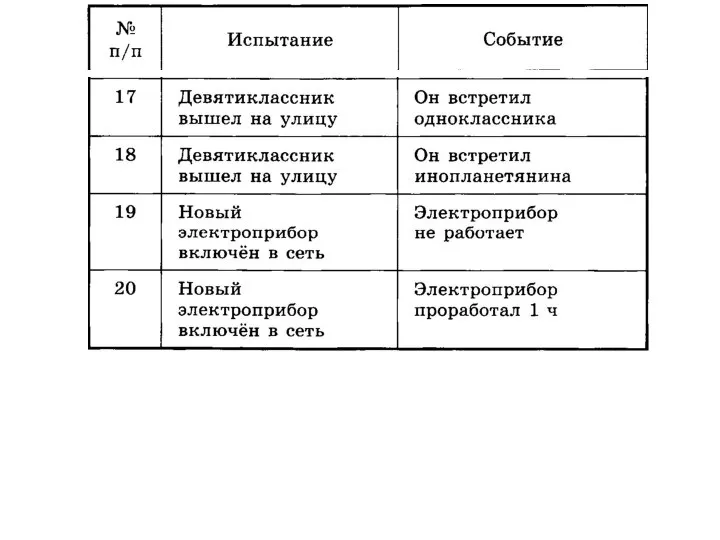
- 34. Укажите, какие из следующих событий – невозможные, достоверные, случайные, а о каких мы можем сказать, что
- 35. Вероятности событий Вероятность события равна сумме вероятностей элементарных событий, благоприятствующих этому событию. P(A)=P(a)+P(b)+P(с)+P(d), где А-событие, а,
- 36. Пример: В шахматной партии, которую Остап Бендер играет с любителем шахмат города Васюки, вероятность выигрыша Остапа
- 37. Пример: Автомобиль подъезжает к перекрестку. Вероятность элементарного события «автомобиль свернет вправо» равна 0,5, вероятность элементарного события
- 38. Равновероятные события События, которые имеют одинаковые вероятности. 25
- 39. Пример: Стрелок один раз стреляет в круглую мишень. При этом вероятность попадания в зоны мишени представлены
- 40. Опыты с равновозможными элементарными событиями Вероятность равновозможных элементарных событий: Р(А)=1/N, где А- элементарное событие, N- число
- 41. 28 Вероятность произвольного события равна отношению числа элементарных событий, благоприятствующих этому событию, к общему числу элементарных
- 44. Скачать презентацию































 Определение знаков коэффициентов K и b в линейной функции по их графикам
Определение знаков коэффициентов K и b в линейной функции по их графикам Графы
Графы Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ
Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ  Векторная алгебра
Векторная алгебра Презентация на тему Геометрическая прогрессия и ее свойство
Презентация на тему Геометрическая прогрессия и ее свойство  Логарифм
Логарифм Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Головоломки и занимательные задачи
Головоломки и занимательные задачи 1_1_matritsy (1)
1_1_matritsy (1) Иллюстрации географических объектов на Луне
Иллюстрации географических объектов на Луне Подобие треугольников. Первый признак подобия
Подобие треугольников. Первый признак подобия Презентация на тему Призма и ее свойства
Презентация на тему Призма и ее свойства  Кратные интегралы
Кратные интегралы Параллельные прямые. Практическая работа
Параллельные прямые. Практическая работа Скрещивающиеся прямые
Скрещивающиеся прямые Плоские деревья и числа Каталана
Плоские деревья и числа Каталана Упрощение логических операций
Упрощение логических операций Прямоугольные треугольники
Прямоугольные треугольники Презентация на тему Проценты
Презентация на тему Проценты  Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Математический анализ. Лекция 1
Математический анализ. Лекция 1 Движение. Поворот
Движение. Поворот Случаи вычитания 11-
Случаи вычитания 11- Слагаемое. Сумма. 1 класс
Слагаемое. Сумма. 1 класс Блез Паскаль
Блез Паскаль Знаки препинания в сложном предложении
Знаки препинания в сложном предложении Выполни вычисления
Выполни вычисления Индивидуальные задания. Урок 15
Индивидуальные задания. Урок 15