Музей математики

мм
МУЗЕЙ МАТЕМАТИКИ
Добро пожаловать в музей математики!

Наверх
Выйти
Зал числа.
Зал близнецов и тройняшек
Зал палиндромов

с
Вниз
Первый шаг к экзамену
Выйти
Зал лучшей находки
Второй шаг к экзамену

Проверь себя
Назад
Найди ошибку

Назад
Ответ

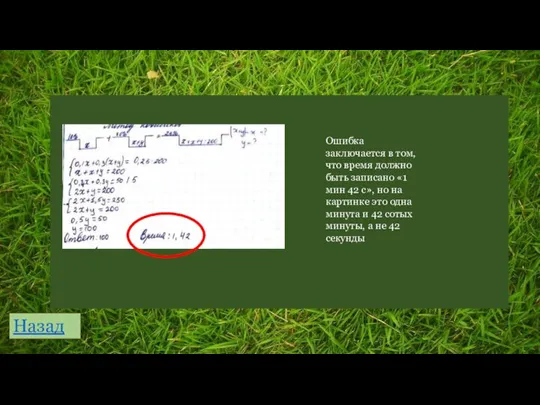
Назад
Ошибка заключается в том, что время должно быть записано «1 мин 42 с», но на картинке это одна минута и 42 сотых минуты, а не 42 секунды

Проверь себя
Назад

Назад
Решение
Решу ЕГЭ №501542
Имеется два сосуда. Первый содержит 100 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 72% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 78% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

Назад

Назад
Решение
Решу ЕГЭ №99578
Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

Назад

Назад
Решение
Решу ЕГЭ №99575
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

Назад

Назад
Решение
Решу ЕГЭ №99575
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Назад

Назад
Решение
Решу ЕГЭ №99573
Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Назад

Назад
Решение
Решу ЕГЭ №99572
Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Назад

Решу ЕГЭ №99571
Назад
В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Решение

Назад

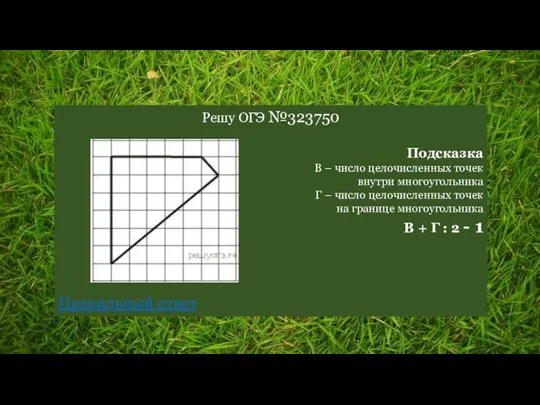
Решу ОГЭ №323750
Подсказка
В – число целочисленных точек
внутри многоугольника
Г – число целочисленных точек
на границе многоугольника
В + Г : 2 - 1
Правильный ответ

Проверь себя
Найди ошибку
Задания для самостоятельной работы
Назад

Леонтий Филиппович Магницкий (1669 — 1739) — русский математик, преподаватель математики в Школе математических и навигацких наук в Москве (с 1701 по 1739), автор первого в России учебного пособия по математике.
Метод Магницкого:
1. Друг под другом записываются содержания веществ имеющихся растворов (смесей/сплавов), слева от них и примерно посередине - содержание вещества в растворе (в смеси/сплаве), который должен получиться после смешивания.
2. Соединить написанные числа прямыми. В каждой паре из большего числа вычесть меньшее, и результат записать в конце соответствующей прямой.
3. Получаемые массовые доли показывают, в каком отношении надо слить исходные растворы (смеси/сплавы).
4. Записать пропорцию и решить её.
Придуманная и составленная им схема напоминает рыбу.
Назад

Назад
Проверь себя

Назад

Решу ЕГЭ №249411
Подсказка
В – число целочисленных точек
внутри многоугольника
Г – число целочисленных точек
на границе многоугольника
В + Г : 2 - 1
Правильный ответ

Назад

Решу ЕГЭ №27554
Подсказка
В – число целочисленных точек
внутри многоугольника
Г – число целочисленных точек
на границе многоугольника
В + Г : 2 - 1
Правильный ответ

Назад

Решу ОГЭ №323790
Подсказка
В – число целочисленных точек
внутри многоугольника
Г – число целочисленных точек
на границе многоугольника
В + Г : 2 - 1
Правильный ответ

Назад

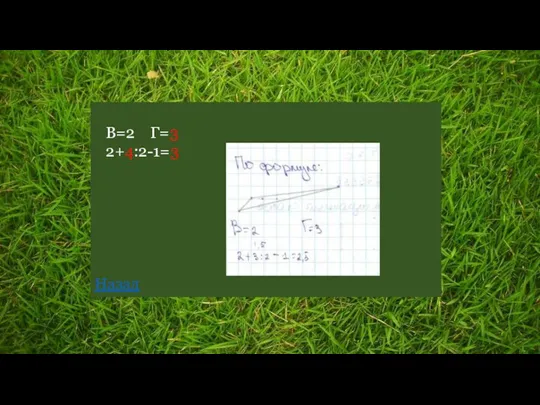
Решу ЕГЭ №248891
Найдите ошибку
Подсказка
В – число целочисленных точек
внутри многоугольника
Г – число целочисленных точек
на границе многоугольника
В + Г : 2 - 1
Правильный ответ

В=2 Г=3
2+4:2-1=3
Назад

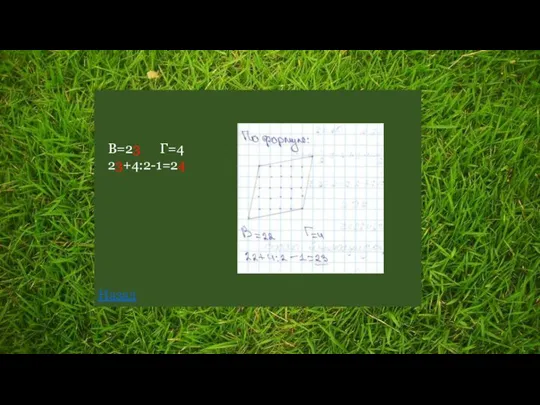
Решу ОГЭ №252617
Найдите ошибку
Подсказка
В – число целочисленных точек
внутри многоугольника
Г – число целочисленных точек
на границе многоугольника
В + Г : 2 - 1
Правильный ответ

В=23 Г=4
23+4:2-1=24
Назад

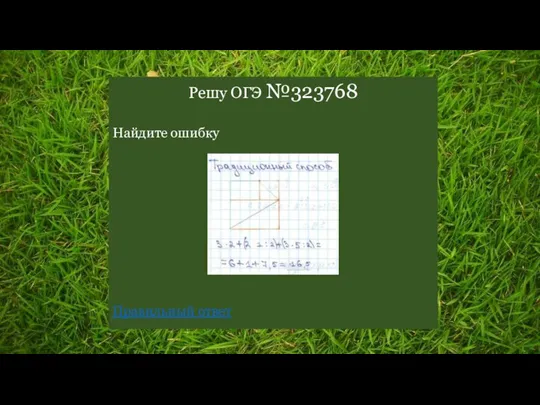
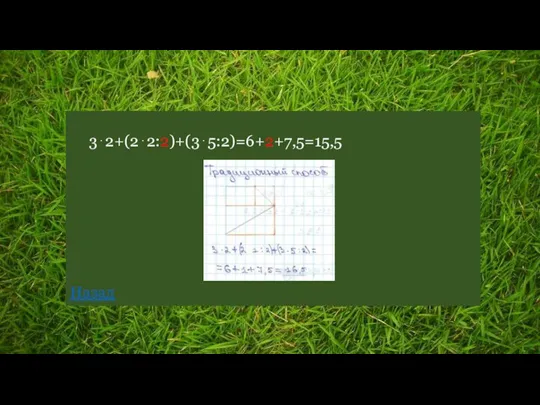
Решу ОГЭ №323768
Найдите ошибку
Правильный ответ

3⋅2+(2⋅2:2)+(3⋅5:2)=6+2+7,5=15,5
Назад

Только в 30-х гг. ХХ века теория решеток получила продолжение в работах Г. Биркгофа. Он показал, что решетка является каркасом для разрозненных достижений во многих математических дисциплинах. Развитие теории решеток связано также и с работами отечественных математиков Г.Ф. Вороного, Б.Н. Делоне и др. В настоящее время теории решеток посвящен целый ряд работ. Некоторые из них изложены в популярной форме и доступны даже учащимся средней школы.
назад

Трагична судьба австрийского математика Георга Александра Пика (10 августа 1859 — 13 июля 1942), родившегося в еврейской семье и умершего в концлагере Терезиенштадт, созданном нацистами в северной Чехии. Открытие формулы Пика, которая позволяет вычислять площади многоугольников с вершинами в узлах квадратной решётки, состоялось в 1899 году. Его долго не замечали после публикации. В 1949 году польский математик Гуго Штейнгауз включил теорему в «Математический калейдоскоп». С этого времени теорема Пика стала широко известна.
У термина «формула Пика» существует и другое значение – «теорема Пика».
Формула Пика (или теорема Пика) — классический результат комбинаторной геометрии и геометрии чисел.
Площадь многоугольника с целочисленными вершинами вычисляется по формуле В + Г/2 -1, где В ⁻⁻ количество целочисленных точек внутри многоугольника, а
Г — количество целочисленных точек на границе многоугольника.
В частности площадь треугольника с вершинами в узлах и не содержащего узлов ни внутри, ни на сторонах (кроме вершин) равна ½.
назад

Решетка на плоскости является средством, которое позволяет задачи алгебры, анализа, теории чисел переводить на геометрический язык.
Первую попытку сделал Дж. Буль в первой половине XIX века. Она привела к понятию булевой алгебры. В конце XIX века Ч. Пирс и Э. Шредер ввели понятие решетки. Их работа не привлекла внимание математической общественности, однако решетка стала для К. Гаусса стартовой точкой для сравнения площади круга с числом точек с целыми координатами, находящимися внутри него. Затем Г. Минковский создал геометрию чисел.
назад

«То общее, чем пользуется любое искусство, а также рассудок и знания, то, что каждый человек должен узнать прежде всего, я называю числом. Высшая Мудрость – это наука о числе», – говорил Платон.
назад

Существует большое количество определений термина "число". О числах первый начал рассуждать Пифагор. Пифагору принадлежит высказывание «Всё прекрасно благодаря числу». По его учению число 2 означало гармонию, 5 – цвет, 6 –холод, 7 – разум, здоровье, 8 –любовь и дружбу. А число 10 называли «священной четверицей»,
так как 10 = 1 + 2 + 3 + 4. Оно считалось священным числом и олицетворяло всю Вселенную.
назад

В толковом словаре С.И. Ожегова определение числа
ЧИСЛО́, -а, мн. числа, -сел, -слам, ср.
1. Понятие количества, величина, при помощи которой производится счёт.
А в толковом словаре русского языка под редакцией Д.В. Дмитриева мне встретились следующие определения: 1.Числом называется единичный элемент математических данных.2. Чётное число – это число, которое кратно 2(делится на 2). 3. Круглые числа – это такие числа, как 10,20 и другие, которые в записи в записи оканчиваются цифрой 0.
назад

Назад
Зал числа

Назад
Зал близнецов и тройняшек

Числовой палиндром — это натуральное число, которое читается слева направо, и справа налево одинаково. А в математике есть палиндром, который называют «числом Шахерезады » от известного произведения “1001 ночь”, где 1001 – число-палиндром. Число знаков может быть и чётным, и нечётным.
В книге «Есть идея!» Мартина Гарднера упоминается «гипотеза о палиндромах». Возьмём любое натуральное число и сложим его с числом, записанным теми же цифрами, но в обратном порядке. Проделаем то же действие с получившейся суммой и будем повторять его до тех пор, пока не получим палиндром. Суть гипотезы в том, что, взяв любое число, после конечного числа действий мы обязательно получим палиндром.
Пример: 13+31=44, 63+36=99, 65+56=121 (двузначные числа); 312+213=525(трёхзначные числа) и пришла к выводу, что не всегда достаточно сделать один шаг, чтобы получить в сумме число перевёртыш, чаще требуется не менее двух. Пример: число 97 порождает палиндром 44044 после выполнения шестого шага.
97+79 = 176; 176 + 671 = 847; 847 + 748 = 1595; 1595 + 5951= 7546;
7546 + 6457 = 14003; 14003 + 30041=44044.
назад

311
113
113
311
31
31 13
313
313 131
назад

Назад
Назад
Зал палиндромов

В нашей школе учатся 4 пары близнецов: братья Кочкуркины, Марк и Никита учатся в начальной школе, в 7 А, где я учусь, сёстры Багиновы, а вот два года назад выпустились в одном классе две пары близнецов - братья Сухопаровы и сестры Горбацевич. Учитель русского языка Жагарина Вера Дмитриевна поделилась со мной сделанной для школьной газеты фотографией. Мне стало интересно, сколько близнецов и тройняшек появилось в нашем районе в 2015 году. За ответом я отправилась в отдел загс и узнала, что в нашем районе в прошлом году родилось 8 пар близнецов и одна тройня.
НАЗАД

Назад
Лучшие находки

Посетив пять магазинов, я решила найти ответ на вопрос: « Верны ли данные на ценниках?». В одном из магазинов нашего города увидела, что порошок «Тайд» продаётся с 50 % скидкой. Проверим… Порошок стоил 439,80 рублей. Цену снизили до 219,90. Указали что скидка 50%. Нужно 439,80 разделить на два. Получится 219,90. Всё правильно. Этот магазин честный.
Посетив ещё один известный магазин в нашем районе, узнаем: порошок стоил 163,50, на него скидка 38%, новая цена 99,90. Проверяем: 163,50:100=1,635 1,635x38=62,13 163,50-62,13=101,37. Магазин сделал скидку больше, чем указал. 163,50-99,90=63,60 63,60:1,635=38,8% Скидка больше на 0,8%.
Кондиционер стоил 132,50, со скидкой 24% цена стала 99,90. Проверяем: 132,50:100=1,325 1,325x24=31,80 132,50-31,80=100,70. Вновь скидку сделали больше. Узнаем, на сколько: 132,50-99,90=32,60 32,60:1,325=24,6%. Скидка больше на 0,6%.
Ещё один пример: масло оливковое стоило 429 рублей. Цену снизили до 279 рублей. Указана скидка 35%. Проверяем: 429:100=4,29 2,29x35=150,15 429-150,15=278,85 279 – 278,85 = 15 копеек. Магазин новую цену округлил с избытком.
Мы посетили четыре магазина, в трёх из них цены указаны неверно.
назад

Ни для кого не секрет, что некоторые автомобилисты стремятся заполучить для своих железных коней «крутые» номера: 100, 500, 900, либо 111, 777, 555, 999 и т.д. Про некоторые из них (наиболее популярные) написаны песни. Мы опросили 100 водителей, в том числе и с номерами репьюнит и репдиджит. Респондентам были заданы вопросы:
Результаты меня удивили. 100% водителей дали отрицательный ответ на первый вопрос, а на второй вопрос мы услышали: «А что это за числа?». В нашей школе есть 5 учителей, которые водят автомобиль, но и среди них никто не дал правильный ответ. А вот три учителя английского языка справились с заданием.
назад