комбинаторика 1 лекция-1

Комбинаторика.
«комбинаторика» происходит от латинского слова combinare – «соединять, сочетать».
Определение. Комбинаторика – это раздел математики, посвящённый задачам выбора и расположения предметов из различных множеств.

Что такое комбинаторика?
3. Комбинаторикой называют область математики, которая изучает вопросы о числе различных комбинаций, которые можно составить из данных элементов.
1. Комбинаторика – это наука о расположении элементов в определенном порядке и о подсчете числа способов такого расположения.
2. Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка).

Как всё начиналось…
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Первоначально комбинаторика возникла в XVI в. в связи с распространением различных азартных игр.
известный немецкий учёный Готфрид Вильгельм Лейбниц.
(1.07.1646 - 14.11.1716)

Основы комбинаторики и теории вероятностей создали и разработали французские математики XVII века Пьер Ферма и Блез Паскаль.
Пьер Ферма (1601-1665)
Блез Паскаль (1623-1662)

После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Абрахам де Муавр и Джеймс Стирлинг нашли формулы для аппроксимации факториала.
Абрахам де Муавр, английский математик (1667-1754)
Джеймс Стирлинг, шотландский математик (1692-1770)

Комбинаторика и ее применение в реальной жизни.
Замечательно, что наука, которая начала с рассмотрения азартных игр, обещает стать наиболее важным объектом человеческого знания. Ведь большей частью жизненные вопросы являются на самом деле задачами из теории вероятностей.
П. Лаплас

Области применения комбинаторики:
лингвистика (рассмотрение вариантов комбинаций букв).
учебные заведения (составление расписаний);
сфера общественного питания (составление меню);

производство (распределение нескольких видов работ между рабочими);
география (раскраска карт);
спортивные соревнования (расчёт количества игр между участниками);

химия (анализ возможных связей между химическими элементами);
агротехника (размещение посевов на нескольких полях);
азартные игры (подсчёт частоты выигрышей);

астрология (анализ расположения планет и созвездий);
биология (расшифровка кода ДНК);
военное дело (расположение подразделений);

доставка почты (рассмотрение вариантов пересылки).
экономика (анализ вариантов купли-продажи акций);
криптография (разработка методов шифрования);

Правило сложения:
Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить m + n способами.
Пример:
На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
Решение:
По условию задачи яблоко можно выбрать
пятью способами, апельсин – четырьмя.
Так как в задаче речь идет о выборе
«либо яблоко, либо апельсин», то его,
согласно правилу сложения, можно
осуществить 5+4=9 способами.
Ответ: 9 способов.

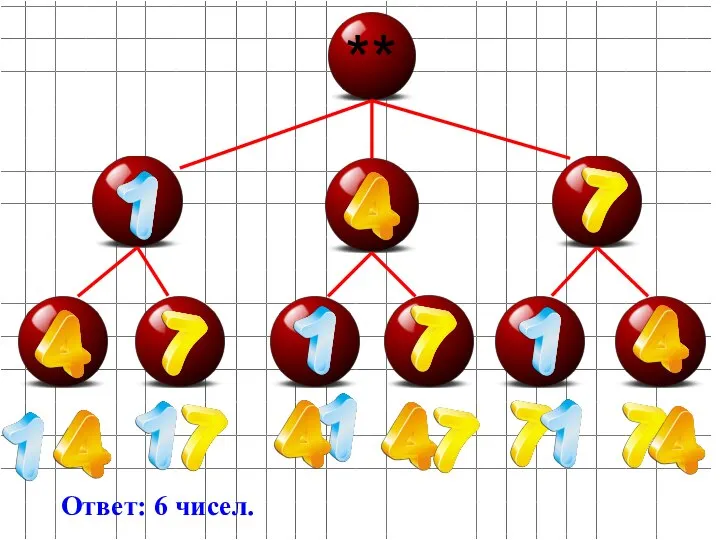
Задача:
Сколько двузначных чисел можно составить из цифр 1,4,7, используя в записи числа каждую из них не более одного раза?
Решение:
1 способ: перебор вариантов.
Для того, чтобы не пропустить и не повторить ни одно из чисел, будем записывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4, и, наконец, с цифры 7:
14, 17, 41, 47, 71, 74.
Ответ: 6 чисел.

Задача:
2 способ: дерево возможных вариантов.
Для этой задачи построена специальная схема.
Ставим звездочку. Далее отводим от звездочки 3 отрезка. Так как в условии задачи даны 3 цифры – 1, 4, 7, то на концах отрезков ставим цифры 1, 4, 7.
Далее от каждой цифры проводим по 2 отрезка. На концах этих отрезков записываем также цифры 1, 4, 7. Получились числа: 14, 17, 41 47, 71, 74. То есть всего получилось 6 чисел. Эта схема действительно похожа на дерево, правда «вверх ногами» и без ствола.

**
Ответ: 6 чисел.

Правило умножения:
Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать п способами, то выбор пары (А, В) в указанном порядке можно осуществить m ∙ п способами.
3 способ решения задачи:
Эту задачу можно решить по-другому и намного быстрее, не строя дерева возможных вариантов. Рассуждать будем так. Первую цифру двузначного числа можно выбрать тремя способами. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать из оставшихся цифр уже двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 3∙2, т.е. 6.
Ответ: 6 чисел.

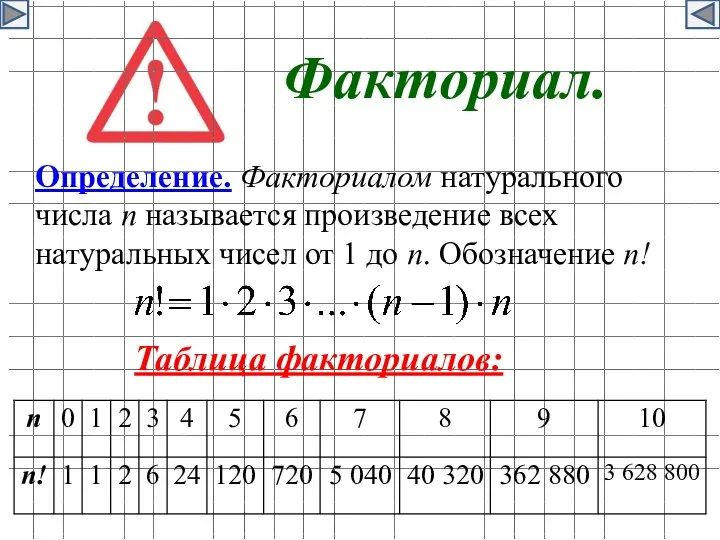
Факториал.
Таблица факториалов:
Определение. Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n. Обозначение n!

Перестановки
Сочетания
Размещения

Перестановки.
Определение. Перестановкой называется конечное множество, в котором установлен порядок элементов.
Число всевозможных перестановок из n элементов вычисляется по формуле:
Pn = n!

Перестановки с повторениями.
Определение .
Число перестановок n – элементов, в котором элементов i –того типа ( ) вычисляется по формуле
Задача: Сколько слов можно составить, переставив буквы в слове «экзамен», а в слове «математика»?
Решение: экзамен – 7 букв ( без повт.) ,
Математика - 10 букв ( с повт. м=2,а=3,т=2,е=и=к=1) ,

Пример 1.
Сколькими способами могут быть расставлены восемь участниц финального забега на восьми беговых дорожках?
Решение: P8 = 8! = 40 320
Пример 2.
Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, причём в каждом числе цифры должны быть разные?
Решение: Р4 – Р3 = 4! – 3! = 18.

Пример 3.
Имеется 10 различных книг, среди которых есть трёхтомник одного автора. Сколькими способами можно расставить эти книги на полке, если книги трёхтомника должны находиться вместе, но в любом порядке?
Решение:

Размещения.
Определение. Размещением
из n элементов
, называют
конечного множества по k, где
упорядоченное множество, состоящее из k
элементов.

Размещения с повторениями.
Определение.
k – размещением с повторениями n–элементного множества называется упорядоченный набор длины k элементов данного множества.
Пример.
2- размещения с повторениями:
Число k – размещений с повторениями вычисляется по формуле:
Задача: Сколько существует номеров машин?

Пример 1.
Из 12 учащихся нужно отобрать по одному человеку для участия в городских олимпиадах по математике, физике, истории и географии. Каждый из учащихся участвует только в одной олимпиаде. Сколькими способами это можно сделать?
Решение:

Пример 2.
Сколько существует семизначных телефонных номеров, в которых все цифры различны и первая цифра отлична от нуля?
Решение:

Сочетания.
Определение. Подмножества, составленные из n элементов данного множества и содержащие k элементов в каждом подмножестве, называют сочетаниями из n элементов по k. (Сочетания различаются только элементами, порядок их не важен: ab и ba – это одно и тоже сочетание).

Равенство:
Число размещений, перестановок и сочетаний связаны равенством:

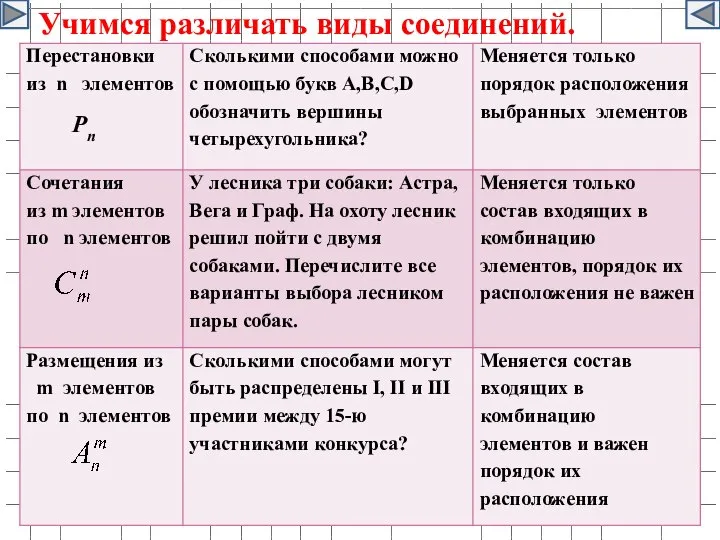
Учимся различать виды соединений.
Pn

Различие между перестановками, размещениями, сочетаниями
В случае перестановок берутся все элементы и изменяется только их местоположение.
В случае размещений берётся только часть элементов и важно расположение элементов друг относительно друга.
В случае сочетаний берётся только часть элементов и не имеет значения расположение элементов друг относительно друга.

Пример 1.
Сколькими способами можно выбрать трёх дежурных из класса, в котором 20 человек?
Решение:

Пример 2.
Из вазы с цветами, в которой стоят 10 красных гвоздик и 5 белых, выбирают 2 красные гвоздики и одну белую. Сколькими способами можно сделать такой выбор букета?
Решение:

Пример 3.
Семь огурцов и три помидора надо положить в два пакета так, чтобы в каждом пакете был хотя бы один помидор и чтобы овощей в пакетах было поровну. Сколькими способами это можно сделать?
Решение:

«Би»-удвоение, раздвоение …
«Ном»(фран. nombre) –номер, нумерация.
«Бином» -»два числа»
Бином Ньютона – это выражение вида
Треугольником Паскаля пользуются при возведении бинома в натуральные степени.
Бином Ньютона.

2) Число всех членов разложения на единицу больше показателя степени бинома, то есть равно (n+l).
3) Сумма показателей степеней a и b каждого члена разложения равна показателю степени бинома,
то есть n.
4) Биномиальные коэффициенты членов разложения, равноотстоящих от концов разложения, равны между собой:
(правило симметрии).
Свойства бинома и биномиальных коэффициентов.

5) Сумма биномиальных коэффициентов всех членов разложения равна .
6) Сумма биномиальных коэффициентов, стоящих на нечетных местах, равна сумме биномиальных коэффициентов, стоящих на четных местах и равна
7) Правило Паскаля: .
Свойства бинома и биномиальных коэффициентов.

8)Любой биномиальный коэффициент, начиная со второго, равен произведению предшествующего биномиального коэффициента и дроби .
Свойства бинома и биномиальных коэффициентов.

Пример .
Доказать, что при любом натуральном n число делится на 9.
Доказательство:
Начнем рассматривать бином в общем виде:
Тогда

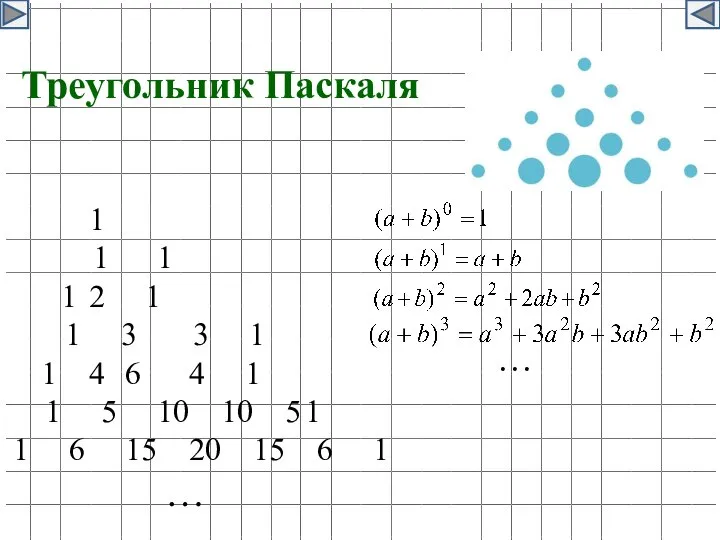
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1 1 5 10 10 5 1
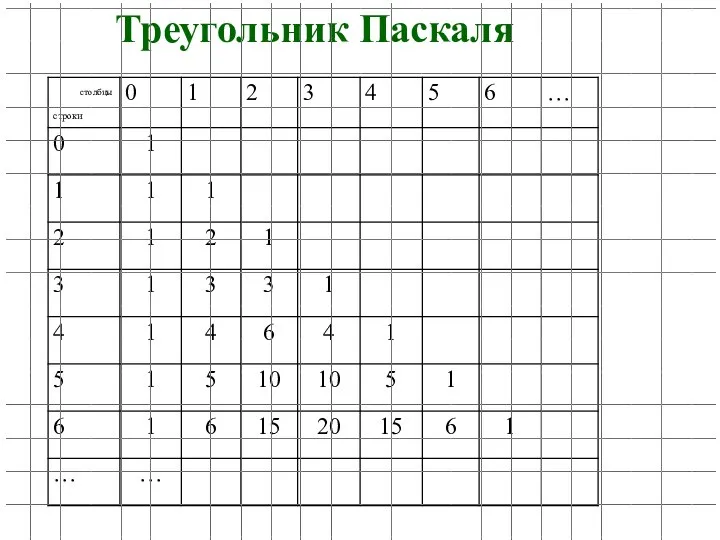
1 6 15 20 15 6 1
…
…
Треугольник Паскаля

Треугольник Паскаля

…
Треугольник Паскаля

Проверь себя
Что такое комбинаторика?
В чём состоит правило суммы?
В чём состоит правило произведения?
Что такое размещения?
Запишите формулу для нахождения числа размещений.
Что такое перестановки?
Запишите формулу для нахождения числа перестановок.
Что такое факториал?
Что такое сочетания?
Запишите формулу для нахождения числа сочетаний.
В чём различие между перестановками, размещениями, сочетаниями?

О пользе комбинаторики или лишних знаний не бывает

1.
2.
отгадай ребусы

3.
4.
5.
отгадай ребусы

Ответы:
Вариант
Сочетания
Факториал
Событие
Исход