Вписанная окружность

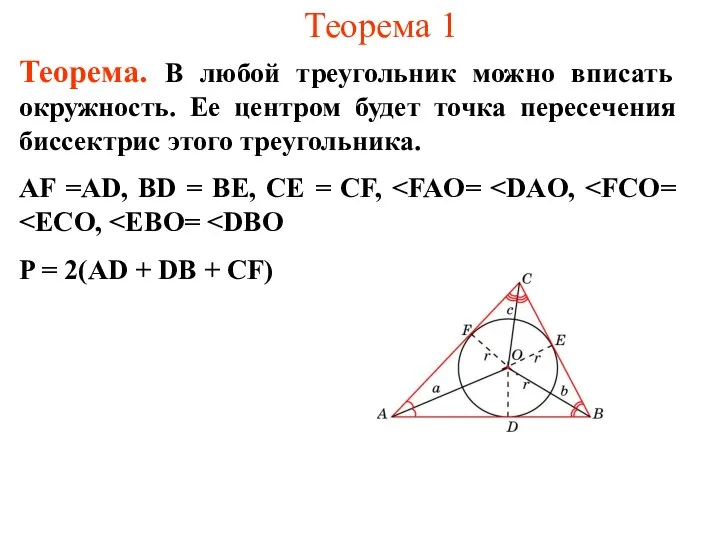
Теорема 1
Теорема. В любой треугольник можно вписать окружность. Ее центром будет точка пересечения биссектрис этого треугольника.
AF =AD, BD = BE, CE = CF,
P = 2(AD + DB + CF)

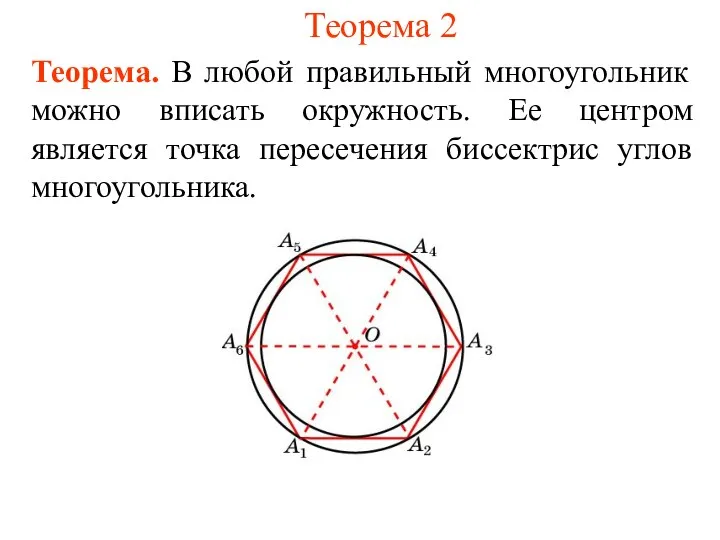
Теорема 2
Теорема. В любой правильный многоугольник можно вписать окружность. Ее центром является точка пересечения биссектрис углов многоугольника.

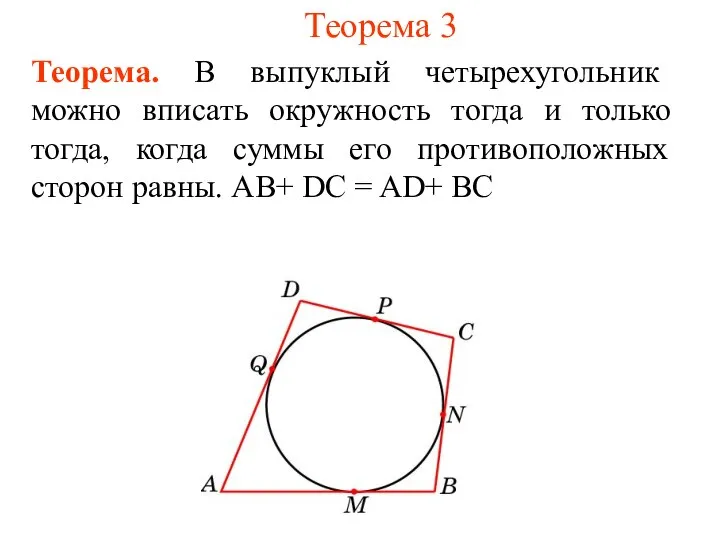
Теорема 3
Теорема. В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны. АВ+ DC = AD+ BC

Вопросы
1.Какая окружность называется вписанной в многоугольник?
2. Во всякий ли треугольник можно вписать окружность?
3. Где находится центр вписанной в треугольник окружности?
4.Можно ли вписать окружность в правильный многоугольник?
5. Может ли центр вписанной в треугольник окружности находиться вне этого треугольника?
6. Можно ли вписать окружность в:
а) остроугольный треугольник;
б) прямоугольный треугольник;
в) тупоугольный треугольник?

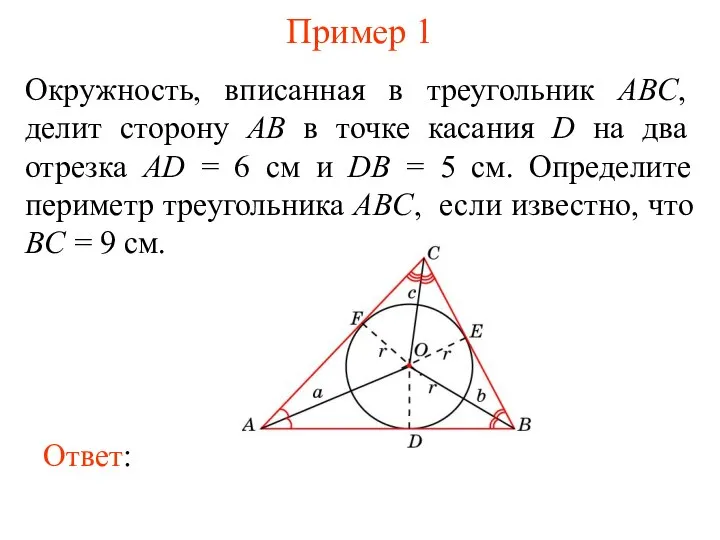
Пример 1
Окружность, вписанная в треугольник ABC, делит сторону AB в точке касания D на два отрезка AD = 6 см и DB = 5 см. Определите периметр треугольника ABC, если известно, что BC = 9 см.
Ответ:

Пример 2
Ответ:
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, которые равны 4 см и 3 см, считая от основания. Определите периметр треугольника.