07.09.22 Огляд елементарних функцій (1)

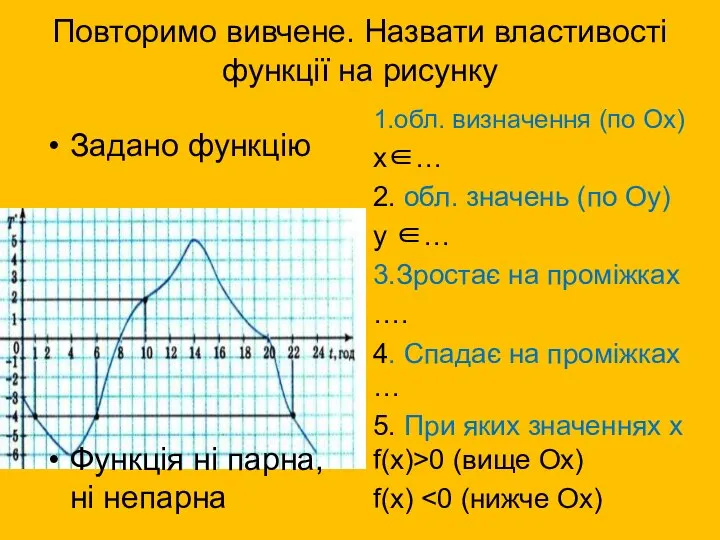
Повторимо вивчене. Назвати властивості функції на рисунку
Задано функцію
Функція ні парна, ні непарна
1.обл. визначення (по Ох)
х∈…
2. обл. значень (по Оу)
у ∈…
3.Зростає на проміжках
….
4. Спадає на проміжках …
5. При яких значеннях х f(x)>0 (вище Ох)
f(x) <0 (нижче Ох)

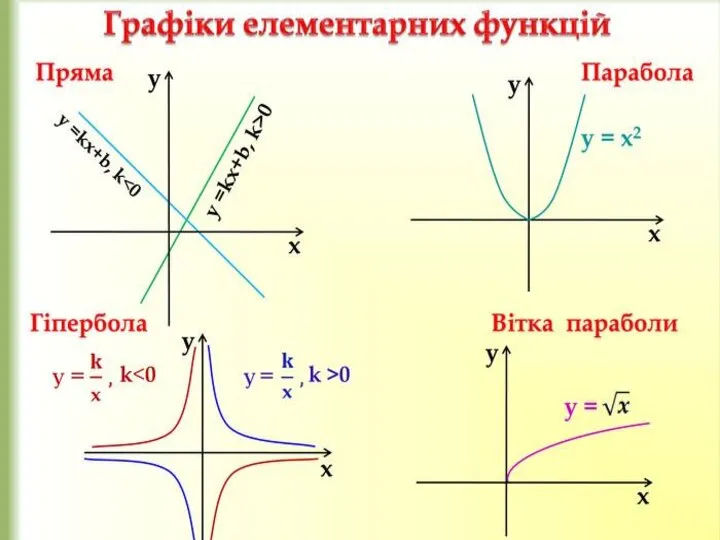
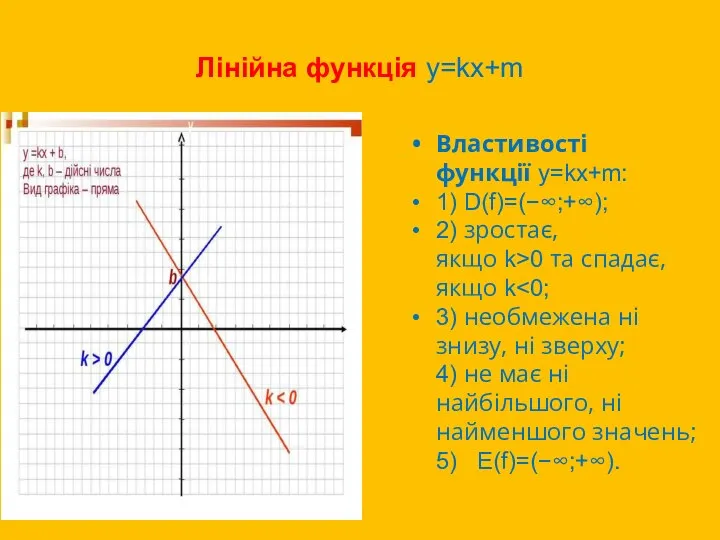
Лінійна функція y=kx+m
Властивості функції y=kx+m:
1) D(f)=(−∞;+∞);
2) зростає, якщо k>0 та спадає, якщо k<0;
3) необмежена ні знизу, ні зверху;
4) не має ні найбільшого, ні найменшого значень;
5) E(f)=(−∞;+∞).

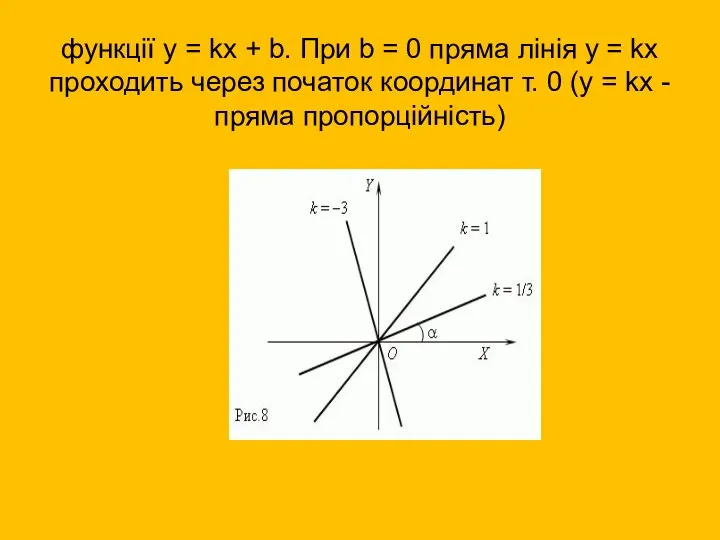
функції y = kx + b. При b = 0 пряма лінія y = kx проходить через початок координат т. 0 (y = kx - пряма пропорційність)

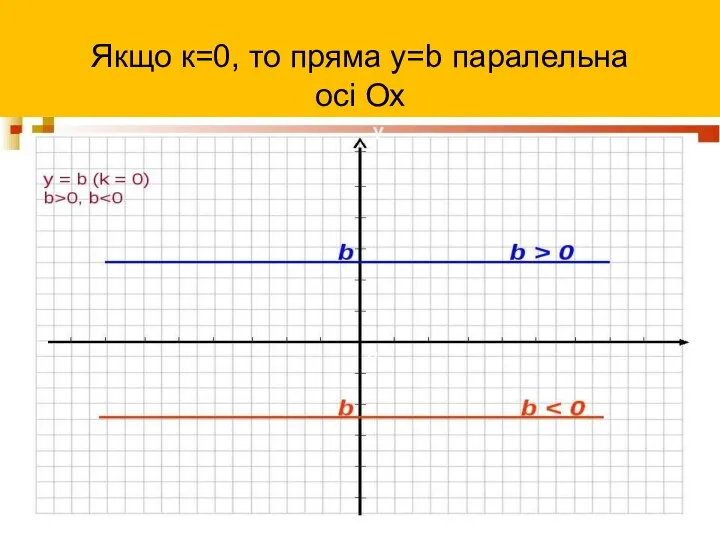
Якщо к=0, то пряма у=b паралельна
осі Ох

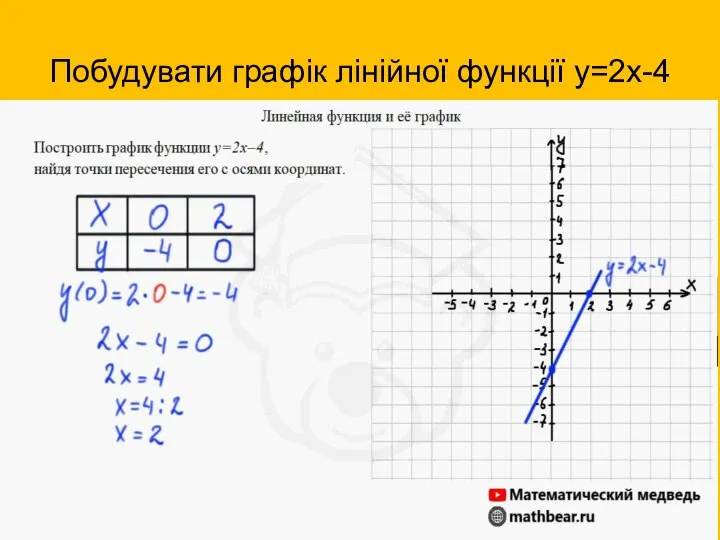
Побудувати графік лінійної функції у=2х-4

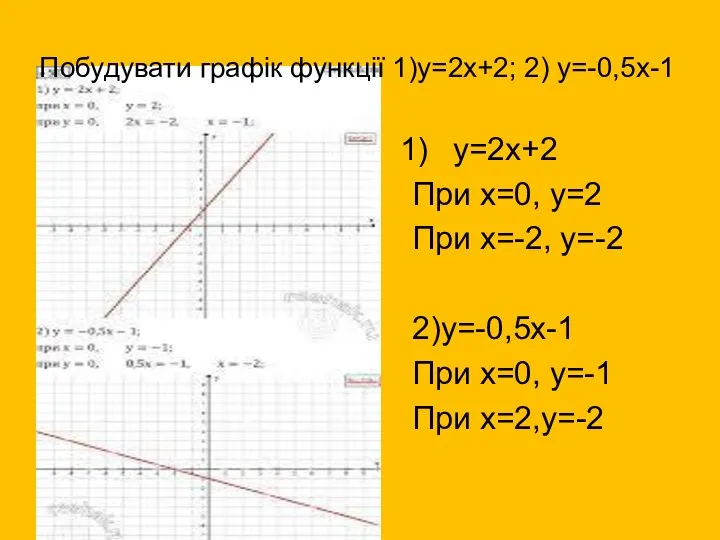
Побудувати графік функції 1)у=2х+2; 2) у=-0,5х-1
у=2х+2
При х=0, у=2
При х=-2, у=-2
2)у=-0,5х-1
При х=0, у=-1
При х=2,у=-2

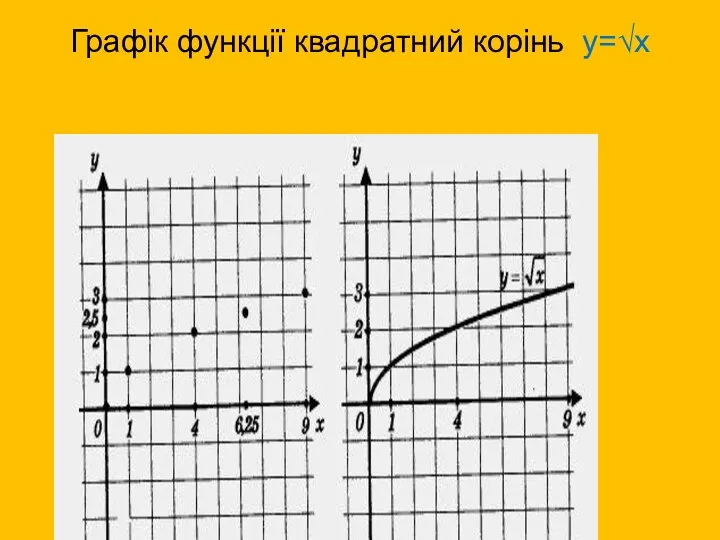
Графік функції квадратний корінь y=√х

Властивості функції y=√х
Властивості функції y=√х
1 D(f)=[0;+∞);
2) зростає;
3) yнайм=0, найбільшого не існує;
4) Ні парна, ні непарна – функція загального виду
5) E(f)=[0;+∞);

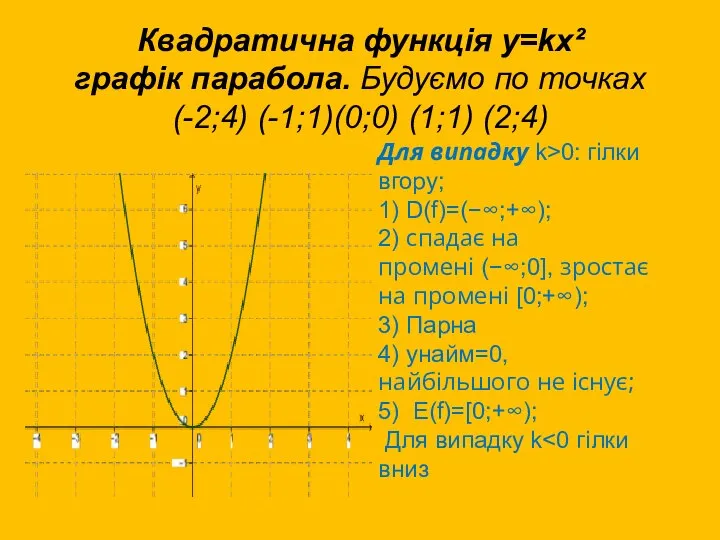
Квадратична функція у=kх²
графік парабола. Будуємо по точках
(-2;4) (-1;1)(0;0) (1;1) (2;4)
Для випадку k>0: гілки вгору;
1) D(f)=(−∞;+∞);
2) спадає на промені (−∞;0], зростає на промені [0;+∞);
3) Парна
4) yнайм=0,
найбільшого не існує;
5) E(f)=[0;+∞);
Для випадку k<0 гілки вниз

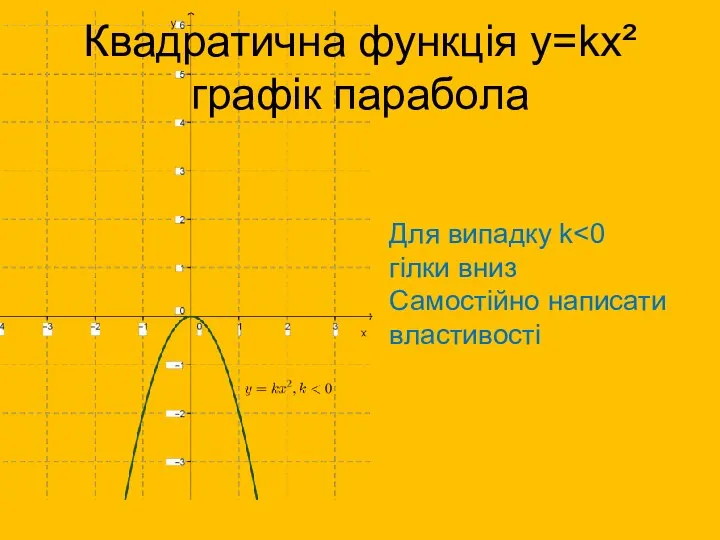
Квадратична функція у=kх²
графік парабола
Для випадку k<0
гілки вниз
Самостійно написати
властивості

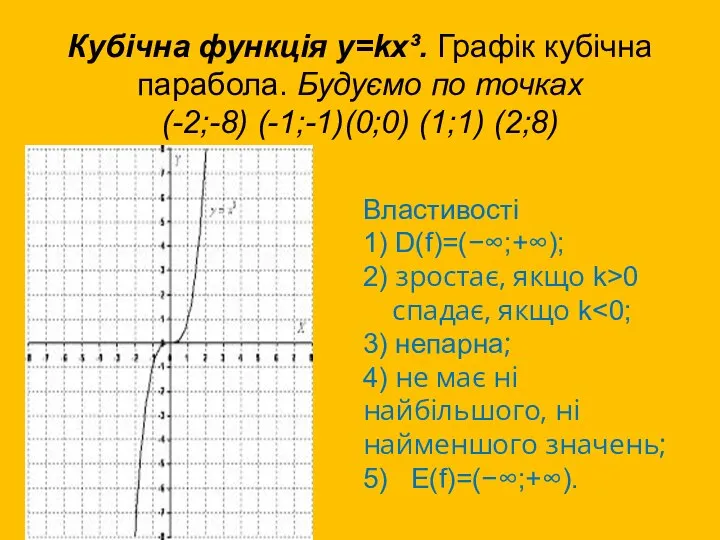
Кубічна функція у=kх³. Графік кубічна парабола. Будуємо по точках
(-2;-8) (-1;-1)(0;0) (1;1) (2;8)
Властивості
1) D(f)=(−∞;+∞);
2) зростає, якщо k>0
спадає, якщо k<0;
3) непарна;
4) не має ні найбільшого, ні найменшого значень;
5) E(f)=(−∞;+∞).

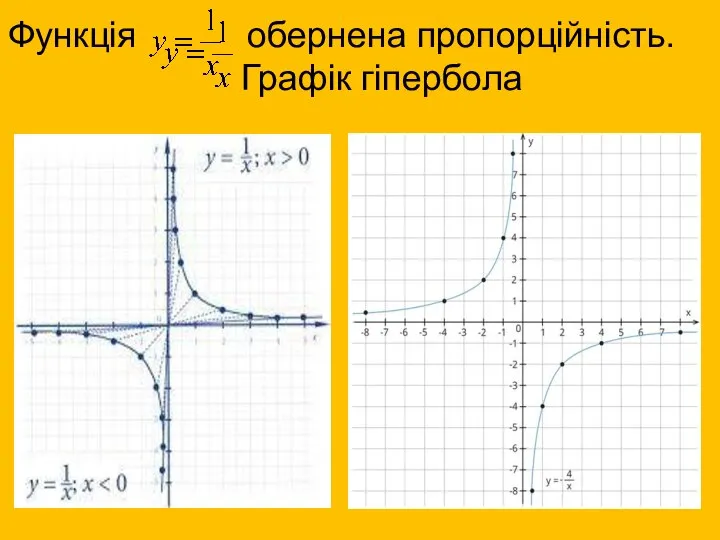
Функція обернена пропорційність.
Графік гіпербола

Властивості функції
D(f)=(−∞;0) ∪ (0;+∞);
2) зростає, якщо k>0
спадає, якщо k<0;
3) непарна;
4) не має ні найбільшого, ні найменшого значень;
5) E(f)=(−∞;+∞).

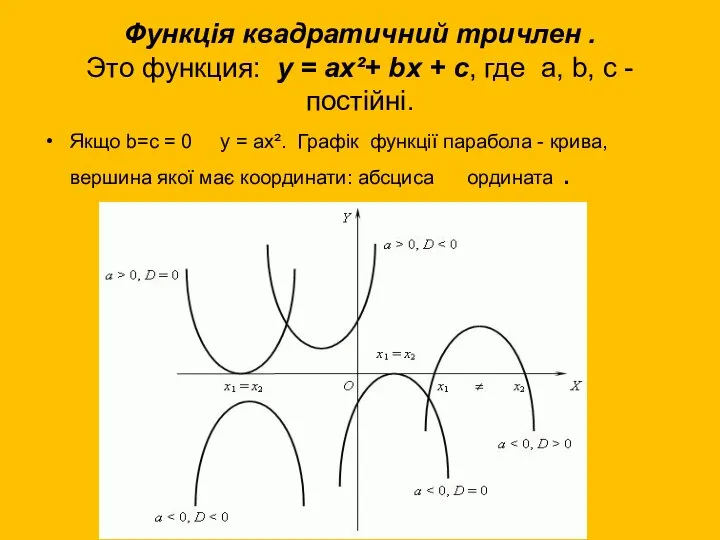
Функція квадратичний тричлен .
Это функция: y = ax²+ bx + c, где a, b, c - постійні.
Якщо b=c = 0 y = ax². Графік функції парабола - крива, вершина якої має координати: абсциса ордината .

Якщо b=c = 0 y = ax². Графік функції парабола - крива, вершина якої має координати:
абсциса ордината
Скільки розвязків має квадраний тричлен в кохному випадку на рис. Попередній слайд?
Що на рис. Нулі функції?