Содержание
- 2. Задачи на оптимизацию – это уже настоящие исследовательские задачи, очень близкие по смыслу (но не по
- 3. 4.решение полученного уравнения, неравенства или системы; 5. интерпретация полученного результата и непосредственно сам ответ на вопрос
- 4. Задача 1. В двух шахтах добывают алюминий и никель. В первой шахте имеется 60 рабочих, каждый
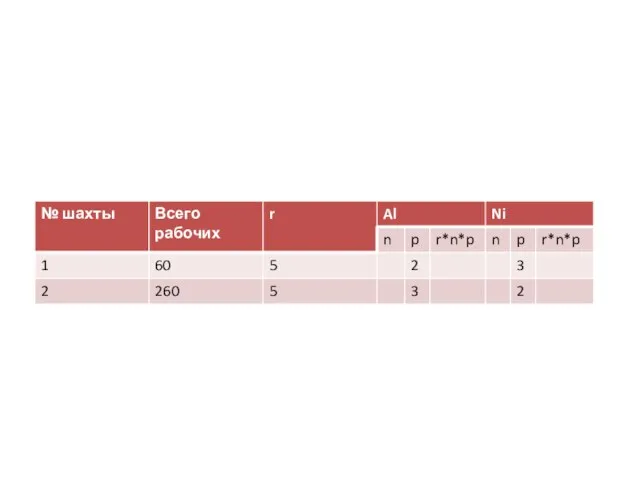
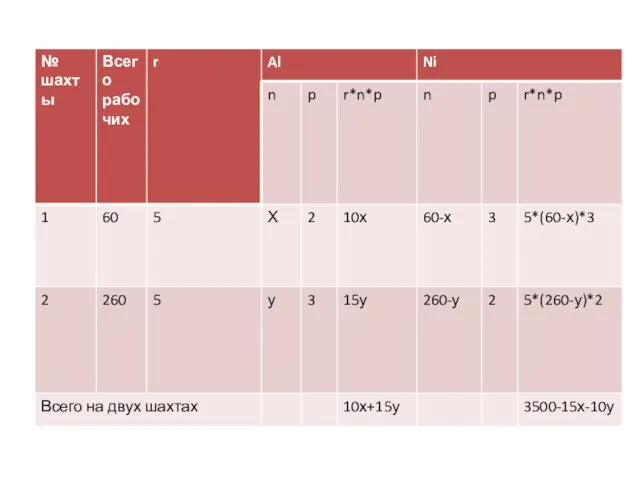
- 5. Решение. Для формализации условия подобных задач введем следующие обозначения и выражения. r – продолжительность рабочего дня;
- 8. Так как для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия
- 9. Учтем ограничения на переменные: Х=175-7/8у≥0 Х=175-7/8у≤60 0≤у≤260 у =200 У=200-8/7х≥0 У=200-8/7х≤260 0≤х≤60
- 10. Составим функцию f ( x , y), которая задает значения массы сплава. Для этого заметим, что
- 11. Задача 2 В двух областях есть по 50 рабочих, каждый из которых готов трудиться по 10
- 12. Задача 3 Баржа грузоподъемностью 134 тонны перевозит контейнеры типов А и В. Количество загруженных на баржу
- 13. Так как количество загруженных на баржу контейнеров типа В должно не менее чем на 25% превосходить
- 14. Суммарная стоимость всех контейнеров, перевозимых баржей при данных условиях: 16∙5+20∙7=220 млн руб. Целесообразно проверить на возможность
- 15. Задача 4 Часть денег от капитала 400 млн руб. размещена в банке под 12 % годовых,
- 16. Пусть х млн рублей инвестировано в производство, тогда 400− x млн рублей — размещено в банк.
- 18. Скачать презентацию













 Презентация на тему Упрощение выражений
Презентация на тему Упрощение выражений  Простые и составные числа
Простые и составные числа Обыкновенные дроби
Обыкновенные дроби Решение линейных систем уравнений способом подстановки
Решение линейных систем уравнений способом подстановки Параллелограмм и трапеция. Урок 3
Параллелограмм и трапеция. Урок 3 Решение задач на проценты. Концентрация
Решение задач на проценты. Концентрация ОГЭ 2022 Математика. Вариант 14
ОГЭ 2022 Математика. Вариант 14 Презентация_к_уроку_Сложение_и_вычитание_алгебраических_дробей_с
Презентация_к_уроку_Сложение_и_вычитание_алгебраических_дробей_с Урок математики по теме: Сложение и вычитание в пределах 20
Урок математики по теме: Сложение и вычитание в пределах 20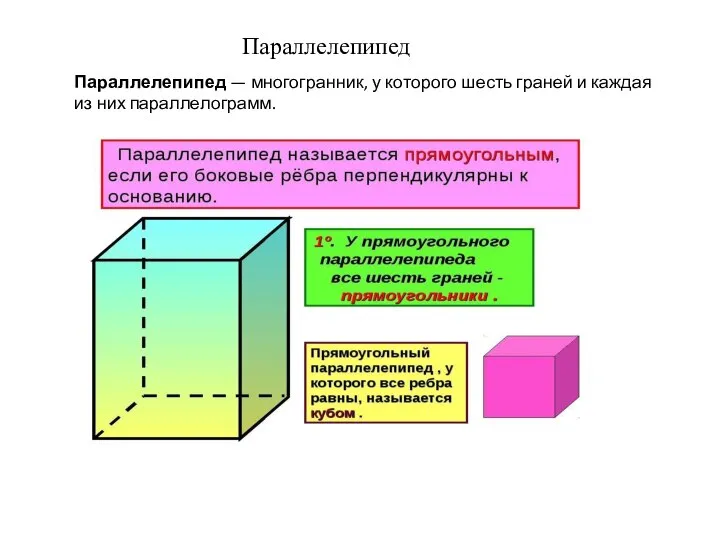 Параллелепипед
Параллелепипед Некоторые свойства функций. (Семинар 2)
Некоторые свойства функций. (Семинар 2) Решение уравнений, содержащих параметры
Решение уравнений, содержащих параметры Сложение и умножение вероятностей
Сложение и умножение вероятностей Перпендикулярность в пространстве. Тест. Практическая часть
Перпендикулярность в пространстве. Тест. Практическая часть Основное свойство дроби
Основное свойство дроби Презентация на тему Многогранники. Призма
Презентация на тему Многогранники. Призма  Пояснения к ЛР № 1
Пояснения к ЛР № 1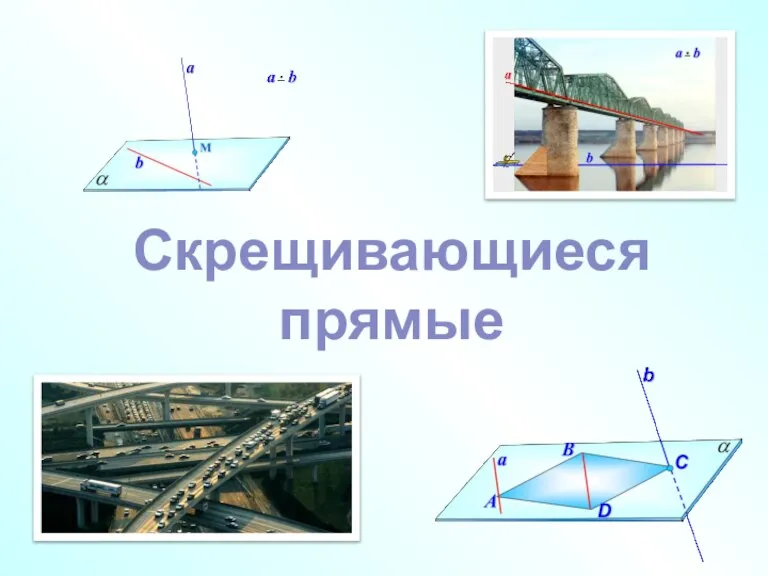 Скрещивающиеся прямые
Скрещивающиеся прямые Доказательство неравенств. Решение задач на доказательство неравенств
Доказательство неравенств. Решение задач на доказательство неравенств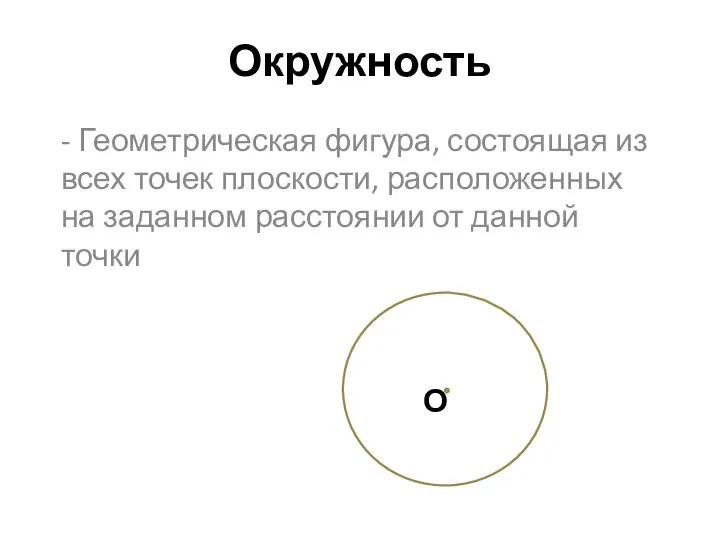 Окружность. Элементы окружности
Окружность. Элементы окружности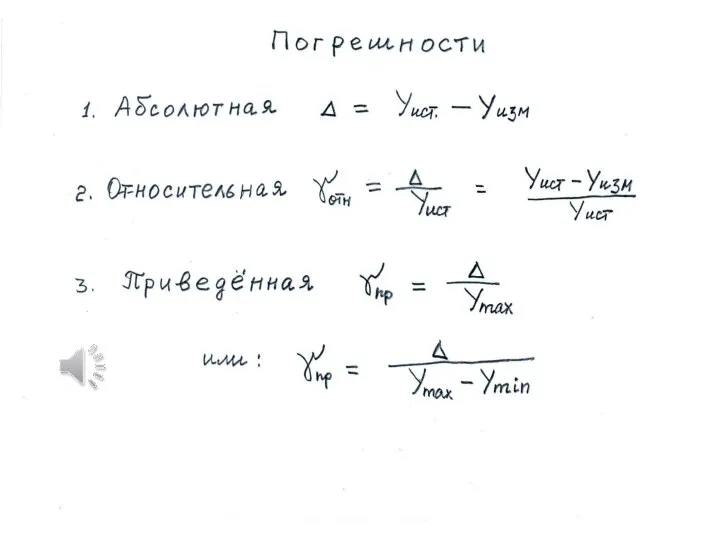 Погрешности. Погрешности измерений
Погрешности. Погрешности измерений Презентация на тему Стандартный вид числа 9 класс
Презентация на тему Стандартный вид числа 9 класс  Перпендикуляр и наклонная к прямой
Перпендикуляр и наклонная к прямой Задачи на проценты
Задачи на проценты Решение тригонометрического уравнения
Решение тригонометрического уравнения Аттестационная работа. Взаимодействие учебной и исследовательской деятельности на уроках математики
Аттестационная работа. Взаимодействие учебной и исследовательской деятельности на уроках математики Призма. Площади поверхностей. Объем призмы
Призма. Площади поверхностей. Объем призмы Приключения Буратино в Стране Финансов
Приключения Буратино в Стране Финансов